Задача №2

3. Задача №2.

2.1. Для определения вида зависимости построим диаграмму рассеяния по имеющимся данным.

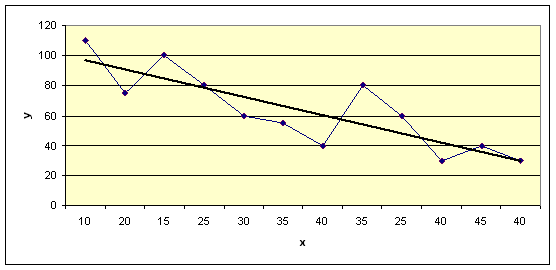
Рис.1. Диаграмма рассеяния и регрессионная прямая, отражающая зависимость инвестиций от объема производства

Расположение точек на диаграмме рассеяния позволяет предположить линейную связь между прибылью предприятия и ставкой налога. Поэтому имеет смысл искать зависимость в виде линейной функции: ŷ = b₀ + b₁х. Очевидно также, что данная зависимость прямая: с увеличением ставки налога прибыль уменьшается.

2.2. В нашем примере при использовании МНК минимизируется следующая функция , т.е. сумма квадратов отклонений эмпирических значений у_iот расчетных значений ŷ_i должно быть минимальным. Согласно МНК для нашего примера воспользуемся следующими формулами расчета:

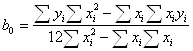
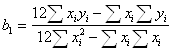
Для нахождения оценок параметров b₀ и b₁ в ручном режиме составим рабочую таблицу, которая содержит исходные данные и промежуточные результаты.

Таблица 4.

Рабочая таблица вычисления оценок параметров уравнения регрессии при изучении зависимости инвестиций от объема производства

I	x	y	x*2	x*y	y2	Yср	e	e2	e/y*100	(x-x ср)2	(у-уср)2	(е-е1)	(е-е)2
1	10	110	100	1100	12100	105,92	4,08	16,65	3,71	400	2177,78	-	-
2	20	75	400	1500	5625	84,62	-9,62	92,54	12,83	100	136,11	-13,7	187,69
3	15	100	225	1500	10000	95,27	4,73	22,37	4,73	225	1344,69	14,35	205,92
4	25	80	625	2000	6400	73,97	6,03	36,36	7,54	25	277,89	1,3	1,69
5	30	60	900	1800	3600	63,32	-3,32	11,02	5,53	0	11,089	-9,35	87,42
6	35	55	1225	1925	3025	52,67	2,33	5,43	4,24	25	69,39	5,65	31,92
7	40	40	1600	1600	1600	42,02	-2,02	4,08	5,05	100	544,29	-4,35	18,92
8	35	80	1225	2800	6400	52,67	27,33	746,93	34,16	25	277,89	29,35	861,42
9	25	60	625	1500	3600	73,97	-13,97	195,16	23,28	25	11,09	-41,3	1705,69
10	40	30	1600	1200	900	42,02	-12,02	144,48	40,07	100	1110,89	1,95	3,80
11	45	40	2025	1800	1600	31,37	8,63	74,48	21,58	225	544,29	20,65	426,42
12	40	30	1600	1200	900	42,02	-12,02	144,48	40,07	100	1110,89	-20,65	426,42
Сумма	360	760	12150	19925	55750	759,84		1493,98	202,78	1350	7616,29	-16,1	259,21
среднее	30,00	63,33	1012,50	1660,42	4645,83	63,32	0,00	124,50	16,90	112,50	634,69	-1,34	21,60

Согласно формулам имеем:

 

 Таким образом, регрессионная модель имеет вид: ŷ=127,22+(-2,13)х.

 у₁= 127,22+(-2,13)*10= 105,92

Для анализа силы линейной зависимости прибыли от ставки налога найдем коэффициент корреляции по формуле:

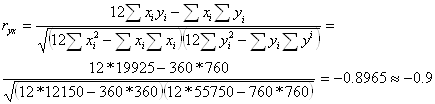
Данное значение коэффициента корреляции позволяет сделать вывод о том, что связи между прибылью и ставкой налога не чуществует.

Средняя относительная ошибка аппроксимации для нашего примера рассчитывается как среднеарифметическая относительных отклонений по каждому наблюдению:

2.3. Стандартная ошибка регрессии характеризует уровень необъясненной дисперсии и для однофакторной линейной регрессии (m=1) рассчитывается по формуле:

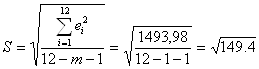
Стандартная ошибка параметра b₁ уравнения регрессии находится по формуле:

Стандартная ошибка параметра b₀ определяется:

На основе стандартных ошибок параметров регрессии проверим значимость каждого коэффициента регрессии путем расчета t-статистик и их сравнении с критическим значением при уровне значимости α=0,05 и числом степеней свободы (12-m-1)=10: t_кр=

Поскольку t_b1 = -6,396<2,228, не подтверждается статистическая значимость коэффициента регрессии b₁.

Поскольку t_b0 =12,75 >2,228, гипотеза о статистической незначимости коэффициента b₀ отклоняется. Это значит, что в данном случае нельзя пренебречь свободным членом уравнения регрессии, рассматривая уравнение:

у=127,22-2,13*х

Коэффициент детерминации в нашем случае рассчитывается по формуле:

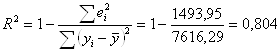
Поскольку R²=0,804<12,75, то можно заключить, что введенный в регрессию фактор – ставка налога- не объясняет поведение показателя – прибыль.

Для оценки автокорреляции остатков рассчитываем значение критерия Дарбина-Уотсона по формуле:

Поскольку значение d меньше 2, то это позволяет сделать предположение о положительной автокорреляции остатков.

Запись полученных характеристик уравнения в стандартной форме имеет вид:

У=127,22-2,13х; r_ху=-0,9; R²=0,804; DW=0,17; А=16,9%

Стандарт ошибка (0,333) (9,98)

t-стат. (-6,396) (12,75)

2.4. При прогнозировании снижения налогового давления до 33% прибыль предприятия составит:

у = 127,22-2,13*33 = 56,93 (тыс.руб.)

4. Задача №3

4.1. Определим переменные модели, ориентируясь на показатели, которые необходимо найти. В задаче требуется определить какое количество нефти из поступающих сортов необходимо переработать, чтобы получить необходимый ассортимент продуктов переработки и максимальную прибыль.

Поэтому введем переменные:

- количество нефти 1 - го сорта, которое идет на изготовление продуктов А, В, С, Д;

- количество нефти 2 - го сорта, которое идет на изготовление продуктов А, В, С, Д;

- количество нефти 3а сорта, которое идет на изготовление продуктов А, В, С, Д;

- количество нефти 3б сорта, которое идет на изготовление продуктов А, В, С, Д;

- количество нефти 4 - го сорта, которое идет на изготовление продуктов А, В, С, Д.

Построим систему ограничений на лимиты по выходу продуктов переработки (по видам) из 1 тонны сырой нефти.

4.2. Учитывая, что в течении недели потребность в продуктах нефтепереработки группы А не превышает 170 тыс. тонн, то ограничение по данному виду выглядит:

0,6+0,5+0,4+0,4+0,3170 тыс. тонн

Ограничение по продуктам нефтепереработки группы В:

0,2+0,2+0,3+0,1+0,385 тыс. тонн

Ограничение по продуктам нефтепереработки группы С:

…+…+…+0,1+…20 тыс. тонн

Ограничение по продуктам нефтепереработки группы Д:

0,1+0,2+0,2+0,2+0,3