Навигация
Мінус 7, буде дев’ять, пишемо 9.7 мінус 5, буде два, пишемо 2, - всього 29
16 мінус 7, буде дев’ять, пишемо 9.7 мінус 5, буде два, пишемо 2, - всього 29.
1.2 Письмове додавання і віднімання трицифрових чисел
Письмове виконання дій першого ступеня розглядають у такій послідовності: додавання і віднімання без переходу через розряд; з одним переходом через розряд і з двома переходами через розряд.
Пояснення нового матеріалу подають на основі аналізу знака розв’язання. Подаємо формулювання деяких завдань, які варто ставити учням, аналізуючи зразки розв’язування:
Розгляньте записи і поясніть, як треба записувати другий доданок при письмовому додаванні.
|
2. Розгляньте записи і поясніть, що треба робити, коли при додаванні одиниць дістаємо десяток або при додаванні десятків дістаємо сотню.
|
|
Розгляньте записи і поясніть, як треба діяти, коли у зменшуваному число одиниць або число десятків дорівнює нулю.
|
|
4. Поясніть, як виконали віднімання з переходом через десяток.
|
|
Наведемо зразки докладного і короткого коментування процесу виконання дій. Розглянемо приклади:
|
|
|
Докладне пояснення до першого прикладу.
До 8 одиниць додати 4 одиниці, буде 12 одиниць, або 1 десяток і 2 одиниці. Дві одиниці пишемо під одиницями, а 1 десяток додаємо до десятків. До 5 десятків додати 7 десятків, буде 12 десятків; 12 десятків та ще 1 десяток, буде 13 десятків, або 1 сотня і 3 десятки.
На місці десятків пишемо 3, а сотню додаємо до сотень. До 3 сотень додати 2 сотні, буде 5 сотень та ще 1 сотня, буде 6 сотень. На місці сотень пишемо 6. У сумі дістали число 632.
Коротке пояснення до третього прикладу.
15 мінус 6 - дев’ять, пишемо 9; 11 мінус 4 - сім, пишемо 7; 2 мінус 1 - пишемо 1; усього 179.
Для кожного випадку дій треба використати достатню кількість вправ тренувального характеру. У процесі розв’язування міркування учнів стають все коротшими, а обчислення - швидшими.
Основою системи вправ є звичайні вирази на одну дію. Їх доповнюють вправи з поясненням, елементами контролю, вимогою вибіркового розв’язування тощо. Наведемо зразки формулювань завдань:
Розв’яжіть приклад ![]() з коментуванням.
з коментуванням.
Розв’яжіть приклад на віднімання ![]() і перевірте розв’язання додаванням.
і перевірте розв’язання додаванням.
Розв’яжіть і порівняйте пари прикладів:
![]()
![]()
![]()
![]()
1.3 Письмове додавання і віднімання багатоцифрових чисел
Учні вже знайомі з письмовим додаванням і відніманням трицифрових чисел, тому ознайомлення з діями в межах мільйона відбувається прямим перенесенням.
Пропонують перевірити правильність розв’язання двох прикладів:
|
|
Учні повторно розв’язують приклади, пояснюють, як треба записувати числа при письмовому додаванні або відніманні.
Після цього вчитель повідомляє, що письмове додавання і віднімання багатоцифрових чисел виконують так само, як додавання і віднімання трицифрових чисел.
Далі учні виконують фронтально чи самостійно різні вправи на застосування дій першого ступеня: обчислення числових виразів з буквеними компонентами; розв’язування рівнянь та різних простих і складених задач.
Перевірка віднімання додаванням. Учитель записує на дошці дві рівності:
![]() ,
,![]()
Учні повинні на числових прикладах обґрунтовувати, чому друга рівність буде правильною. Потім учитель повідомляє: якщо додати різницю і від’ємник, то дістанемо зменшуване. Цей зв’язок використовують для перевірки правильності виконання дії віднімання.
Міркуємо так: якщо при додаванні різниці і від’ємника не дістанемо зменшуваного, то в обчисленнях допущено помилку.
Аналогічно на наступному уроці розглядають перевірку додавання відніманням. Тут використовують зв’язок: якщо ![]() , то
, то ![]() . Запис перевірки учні записують поряд з прикладом на віднімання. Слово “перевірка” записувати не треба.
. Запис перевірки учні записують поряд з прикладом на віднімання. Слово “перевірка” записувати не треба.
|
|
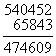
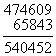
У процесі розв’язування прикладів з коментуванням пояснюють обчислення різниці, коли у зменшуваному є кілька нулів; додавання кількох доданків; знаходження значень виразів -![]() на сумісні дії першого ступеня та виразів з дужками.
на сумісні дії першого ступеня та виразів з дужками.
Наведемо один із зразків такого коментування.
Треба від числа 3005 відняти 1126. Від 5 одиниць відняти 6 одиниць не можна. Оскільки у розрядах десятків і сотень 0 одиниць, то візьмемо 1 тисячу. Щоб не забути про це, у розряді тисяч поставимо крапку. Одна тисяча - це 10 сотень.9 сотень залишимо у розряді сотень, а одну сотню перетворимо у десятки. Одна сотня - це 10 десятків, 9 десятків залишимо в розряді десятків, а один десяток перетворимо в одиниці.1 десяток - це 10 одиниць. Та ще 5 одиниць, буде 15 одиниць. Від 15 одиниць відняти 6 одиниць, буде 9 одиниць. Пишемо 9 на місці одиниць. Від 9 десятків відняти 2 десятка, буде 7 десятків. Пишемо 7 на місці десятків. Від 9 сотень відняти 1 сотню, буде 8 сотень. Пишемо 8 на місці сотень. Від 2 тисяч відняти 1 тисячу, буде 1 тисяча. На місці тисяч пишемо 1. Різниця дорівнює 1879.
Додавання і віднімання складених іменованих чисел виконують, перетворивши їх у прості іменовані числа. Після цього дії над ними виконують так само, як і над натуральними числами. Проте учням слід вказати на можливість виконання дій відразу складеними іменованими числами. Пояснення дають за зразками запису розв’язання.
![]()
|
|
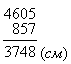
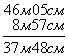
2. Цікаві задачі
1. Маса новонародженого слоненяти 130кг, він на 1870кг легший за дитинча синього кита. Яку масу має новонароджений синій кит?
Сл. - 130кг, на 1870кг легший.
К. -?
|
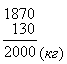
Відповідь: маса новонародженого синього кита - 2 тонни.
2. Довжина річки Дніпро 2285км, а річки Дністер - 1410км. На скільки кілометрів Дніпро довший від Дністра?
|
Дністер - 1410км
|
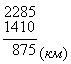
Відповідь: на 875км довший Дніпро.
3. У трьох шафах 2640 книжок. У першій і другій шафах разом 1710 книжок, а в другій і третій - 1820 книжок. Скільки книжок у кожній шафі?
|
|
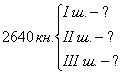
|
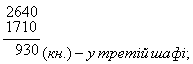
|
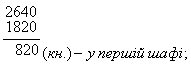
|
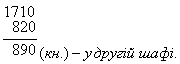
Перевірка:
|
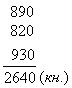
Відповідь: у першій шафі - 820 книжок, у другій шафі - 890 книжок, у третій шафі - 930 книжок.
4. Для поливання шкільної ділянки було заготовлено два баки води: в одному 45 відер, у другому - 33. За один і той самий час з кожного бака води забирали порівну. Скільки води залишилося в другому баці, якщо в першому залишилося 18 відер?
І б. - 45 в.
ІІ б. - 33 в.
Залишилося - 18 в. в першому баці.
|
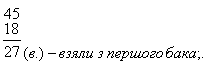
|
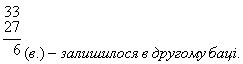
Відповідь: 6 відер води.
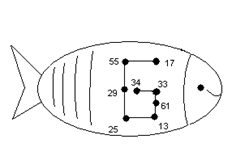
5. Батькові 39 років, а синові 14. Скільки років дочці, якщо через 16 років синові та дочці разом буде стільки років, скільки батькові?
Через 16 років батькові буде 55 років (39+16=55), а синові 30 (14+16=30). Отже, дочці буде 25 років (55-30=25). Тепер їй 9 років (25-16=9).
Похожие работы
... Врахування пам’яті, уваги та уяви, мислення, інших психічних процесів, а також вікових та індивідуальних особливостей необхідне для вдумливої організації самостійної роботи на уроці. Розділ ІІ. Способи організації самостійної роботи в малокомплектній школі та перевірка їх ефективності ІІ.1 Способи організації самостійної роботи Самостійна робота на уроці – органічна частина навчального ...
... ість є одним із основних напрямів активізації навчання молодших школярів. Тому самостійна робота є ефективним методом навчання у початковій школі, підвищуючи інтерес учнів до навчального предмета та розвивають активність учнів. Окрім того, використання самостійних робіт сприяє формуванню самостійності як риси характеру молодших школярів. Протягом усього періоду навчання у початковій школі вчителі ...
... здійснювати на ведучому навчальному матеріалі. 6. Формування прийомів розумової діяльності вимагає врахування індивідуально-вікових особливостей учнів. 1.2 Формування уміння порівнювати в процесі навчання математики Порівняння в навчанні – це розумова операція, за допомогою якої встановлюються риси подібності і відмінності між визначеними предметами і явищами. Пізнання будь-якого ...
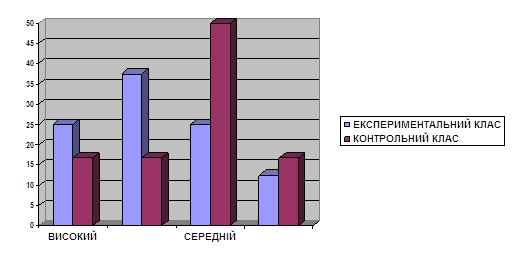
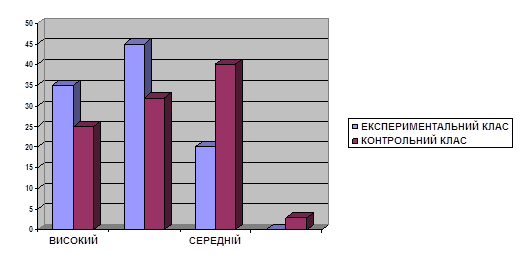
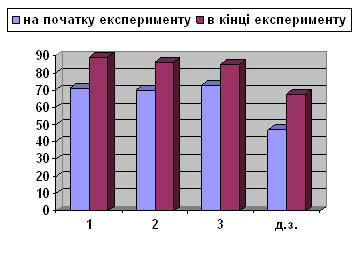
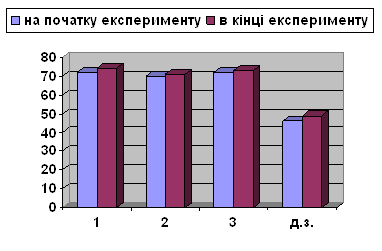
... 2 А клас (експериментальний клас) Правильно виконали (у %) № завдання Діаграма 2. 2 Б клас (контрольний клас) Правильно виконали (у %) № завдання Аналізуючи одержані результати експериментального дослідження можна зробити висновок, що дидактична гра – це ефективний метод навчання математики молодших школярів. Ігри та ігрові ситуації допомагають учням у навчанні, органі ...



0 комментариев