Объяснение нового материала

3.  Объяснение нового материала.

Преподаватель: Сущность метода пересечений состоит в следующем:

Задачу сводят к построению одной точки (основной элемент построения), которая удовлетворяет двум условиям a₁ и a₂.

Пусть Ф₁ – множество точек, удовлетворяющих условию a₁, а Ф₂ – удовлетворяющих a₂. Тогда точка x будет являться пересечением двух множеств точек Ф₁ и Ф₂. Чтобы построить точку x необходимо, опустив условие a₂, построить множество точек Ф₁, удовлетворяющих условию a₁, затем, опустив условие a₁, построить множество точек Ф₂, удовлетворяющих a₂. Пересечение этих двух множеств точек и будет искомый элемент x.

Рассмотрим пример:

Задача 1 (решается вместе с преподавателем)

Построить окружность данного радиуса r, проходящую через данную точку А и касающуюся данной прямой d.

Анализ. Предположим, что задача решена и окружность (О, r) построена.

Так как радиус этой окружности дан, то мы сможем её построить, если будет построен её центр О. Точка О удовлетворяет двум условиям:

а) r(О, r) = r;

б) r(O, d) = r.

Условие а) определяет фигуру S (A, r), а условие б) d₁ и d₂ – такие прямые, что r(d₁, d) = r(d, d₂) = r

Построение:

1)  S (A, r);

2)  прямые d₁ и d₂:r(d₁, d) = r(d, d₂) = r;

3)  ОÎS (A, r) Ç {d₁, d₂};

4)  S (O, r).

Доказательство:

а) ОÎS (A, r) => AÎ S (O, r);

б) ОÎ{d₁, d₂} => r(O, d) = r => S (O, r) касается прямой d.

Исследование:

Построения 1 и 2 всегда выполнимы. Рассмотрим построение 3.

Здесь возможны три случая:

а) r(А, d) < 2r => Фигура S (A, r) Ç {d₁, d₂} состоит из двух точек;

Задача имеет два решения.

б) r(А, d) = 2r => Фигура S (A, r) Ç {d₁, d₂} – точка, задача имеет одно решение.

в) r(А, d) > 2r => S (A, r) Ç {d₁, d₂} = Æ; задача не имеет решений.

Задача 2

Построить треугольник АВС, зная АС и радиусы окружностей, описанных около треугольников АВD и ADC, где AD высота.

Анализ: Известно, что радиус описанной окружности лежит на пересечении серединных перпендикуляров. Так как АС известно, радиусы окружностей известны, точка М – середина АD. Следовательно, можно построить и AD.

Построение:

1.  АС, О₂ – середина;

2.  w₁(О₂, r₂);

3.  w₂(A, r);

4.  w₃(O₁, r);

5.  CDÇw₃ = B;

6.  ABC – искомый;

Доказательство:

r₁ – радиус описанной окружности треугольника АВD (по построению).

Исследование:

Радиусы описанных окружностей должны быть равны половине гипотенузы. Решение единственное.

4.  Домашнее задание

Оставшиеся задачи и предложенная теория.

Занятие 4

Тема: Решение задач на построение алгебраическим методом

Цель: Сформировать умение строить отрезки по данным формулам.

Оборудование: Циркуль, линейка.

План-коспект занятия:

1. Организационный момент.

2. Объяснение нового материала

Преподаватель: При решении задач алгебраическим методом приходится решать следующую задачу:

Даны отрезки a, b,…, l, где a, b,…, l – их длины. Выбрана единица измерения. Требуется построить отрезок х, длина которого х в этой же системе измерения выражается через длины a, b,…, l заданной формулой:

x = f (a, b,…, l)

Рассмотрим построение отрезков, заданных следующими простейшими формулами:

1) ;

2)

3) 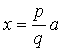 , где p и q – натуральные числа;

4)   (построение отрезка – четвёртого пропорционального к данным трём).

5)  ;

6)  ;

7) 

С помощью построений 1–7 можно строить отрезки, заданные более сложными формулами.

Рассмотрим пример: (решить вместе с преподавателем).

Пример 1. Пусть а, b, c и d – данные отрезки. Построить отрезок х, заданный формулой:

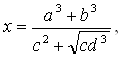
Решение: Построение отрезка выполняем в следующей последовательности:

1.  Строим отрезок у, заданный формулой (для этого дважды выполняем построение отрезка, заданного формулой 5);

2.  Строим отрезок z, заданный формулой

(построение отрезка, заданного формулой 6);

3.  Строим отрезки u и v по формулам  и

(построение отрезка по формуле 4);