Навигация
Решение задач на построение в курсе геометрии основной школы как средство развития логического мышления школьников
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Вятский государственный гуманитарный университет»
Физико-математический факультет
Кафедра дидактики физики и математики
Выпускная квалификационная работа
Решение задач на построение в курсе геометрии основной школы как средство развития логического мышления школьников
Выполнила студентка V курса
физико-математического факультета Коновалова Вера Сергеевна
Научный руководитель: к. пед. н.,
доцент кафедры дидактики физики и математики Шилова З.В.
Рецензент: к. пед. н., ст. преп.
кафедры дидактики физики и математики Зеленина Н.А.
Работа допущена к защите в ГАК
«___» _________2008 г. Зам. зав. кафедрой __________ М.В. Крутихина
«___» _________2008 г. Декан факультета ____________ Е.В. Кантор
Киров 2008
Содержание
Введение
1. Анализ учебной и учебно-методической литературы по геометрии
1.1. Анализ учебников по геометрии основной школы
1.2. Анализ учебно-методической литературы
2. Логическое мышление: основные понятия.Анализ психолого-педагогической литературы
2.1. Природа и виды мышления
2.2. Развитие мышления ребенка
2.3. Понятие логического мышления
2.4. Развитие логического мышления школьников в процессе обучения математике
3. Методика решения задач на построение
3.1. Анализ
3.2. Построение
3.3. Доказательство
3.4. Исследование
3.5. Методические рекомендации по обучению решению задач на построение
4. Методы решения задач на построение
4.1. Метод геометрических мест
4.2. Методы геометрических преобразований
4.2.1. Метод центральной симметрии
4.2.2. Метод осевой симметрии
4.2.3. Метод параллельного переноса
4.2.4. Метод поворота
4.2.5. Метод подобия
4.3. Алгебраический метод
5. Опытное преподавание
Заключение
Библиографический список
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
Приложение 6
Введение
Геометрические задачи на построение, возможно, самые древние математические задачи. Кому-то они сейчас могут показаться не очень интересными и нужными, какими-то надуманными. И в самом деле, где и зачем может понадобиться умение с помощью циркуля и линейки построить правильный семнадцатиугольник или треугольник по трем высотам, или даже просто сделать построение параллельной прямой. Современные технические устройства сделают все эти построения и быстрее, и точнее, чем любой человек, а заодно смогут выполнить и такие построения, которые просто невозможно выполнить при помощи циркуля и линейки.
И все же без задач на построение геометрия перестала бы быть геометрией. Геометрические построения являются весьма существенным элементом изучения геометрии. Однако, анализ содержания школьного математического образования позволил выявить ряд недостатков в обучении школьников:
1. Наметилась четкая тенденция к сокращению количества задач на построение в школьном курсе математики. Это объясняется тем, что значительно сужена роль задач на построение, которая соответствует целям обучения, таким как развитие мышления и воспитание учащихся, и проявляется в виде воздействия на мышление учеников, в первую очередь на логическое. В большинстве случаев, считается, что главная и единственная цель обучения решению таких задач – это формирование практических умений и навыков построения основных геометрических фигур: треугольников, перпендикуляров, биссектрис и т. п., то есть основное внимание уделяется практическому значению задач, при этом совершенно не рассматривается вопрос развития логического мышления учеников и возможности использования задач на построение при изучении геометрии.
2. Знания учащихся по данной теме нередко носят формальный характер, наблюдается отсутствие структурности. Так, при изучении задач на построение единственное, что требует учитель – это знание соответствующих алгоритмов построений. При этом не объясняется, как получен данный алгоритм. Поэтому ученик вынужден запоминать материал без понимания.
3. В настоящий момент в школе недостаточно уделяется внимания рассмотрению таких основных методов решения задач на построение как метод преобразований, алгебраический метод, метод геометрического места точек.
4. У учащихся нет четкого представления об этапах решения задач на построение: анализе, построении, доказательстве и исследовании, которые точно соответствуют этапам любого логического рассуждения. Практически не уделяется внимание одному из важных этапов – исследованию, в котором учащиеся зачастую не видят смысла, несмотря на то, что он, в свою очередь, является хорошим средством развития логического мышления.
Перечисленные выше недостатки и определили проблему исследования.
Проблема исследования заключается в рассмотрении на основе психологии, педагогики и методики преподавания математики возможности развития логического мышления учащихся при решении задач на построение в курсе основной школы.
Цель исследования: разработать методические рекомендации при решении задач на построение, способствующие развитию логического мышления учащихся.
Объект исследования: процесс обучения геометрии учащихся в курсе основной школы.
Предмет исследования: процесс обучения решению задач на построение.
Гипотеза: применение разработанных методических рекомендаций при решении задач на построение будут способствовать наиболее эффективному развитию логического мышления учащихся при обучении геометрии в курсе основной школы.
Задачи:
1) провести анализ учебных программ, учебной и учебно-методической литературы;
2) рассмотреть понятие логического мышления;
3) рассмотреть основные этапы решения задач на построение;
4) разработать методические рекомендации по обучению решению задач на построение;
5) рассмотреть методы решения задач на построение;
6) осуществить опытное преподавание.
Методы исследования:
1) анализ учебной, учебно-методической, психолого-педагогической литературы;
2) наблюдение;
3) анкетирование;
4) проведение психологических методик;
5) проведение опытного преподавания.
1. Анализ учебной и учебно-методической литературы по геометрии
Нами был предварительно проведен и анализ программы по математике (см. Приложение 1).
А также анализ учебников по математике для 5-6 классов.
1) Н.Я. Виленкин “Математика 5” [12]: в учебнике две главы “Натуральные числа” и “Дробные числа”, каждая содержит четыре параграфа. В нем первым из построений с помощью линейки (Глава 1,§1) является построение отрезка (далее уже многоугольника). А также изучается сравнение отрезков с помощью циркуля. Далее идет изучение прямой и луча. Следующие построения рассматриваются в начале второй главы в пункте окружность и круг. А именно построение окружности с помощью циркуля. В конце курса школьники учатся обращаться с чертежным треугольником (построения прямого угла).
Н.Я. Виленкин “Математика 6” [13]: в этом учебнике также две главы “Обыкновенные дроби” и “Рациональные числа”, каждая содержит четыре параграфа. В конце курса учащиеся знакомятся с перпендикулярными и параллельными прямыми и строят их с помощью чертежного треугольника и линейки.
2) Г.В. Дорофеев “Математика 5” [14]: в данном учебнике первым из построений с помощью линейки является построение прямой, проходящей через две данные точки, а также построение окружности с помощью циркуля. Далее следует изучение луча и сравнения отрезков с помощью циркуля. В следующей главе рассматривается понятие угла и его построение, в том числе с помощью угольника. Третья глава посвящена изучению многоугольников, в частности прямоугольников и треугольников.
Г.В. Дорофеев “Математика 6” [15]: в главе 2 ‘Прямые и окружности’ знакомит учащихся с перпендикулярными и параллельными прямыми, и их построением с помощью угольника и линейки. Далее определяются касательная к окружности, концентрические окружности, и рассматриваются варианты взаимного расположения прямой и окружности, двух прямых на плоскости. Предлагаются различные задачи на построение касательной к окружности; окружности, касающейся двух параллельных прямых; двух окружностей. Одна из глав учебника посвящена изучению симметрии: осевой и центральной. Предлагаются задачи на построение симметричных фигур, а также на нахождение кратчайшего пути. Также имеется глава, посвященная фигурам на плоскости, в частности треугольникам и параллелограммам. В ней рассматривается построение треугольника по трем сторонам и предлагаются задачи на построение различных треугольников (прямоугольных, равнобедренных, остроугольных, тупоугольных).
1.1 Анализ учебников по геометрии основной школы1) Л.С. Атанасян, В.Ф. Бутузов [7]
а) 7 класс: содержит четыре главы. Тема “Задачи на построение” изучается в конце главы 2 “Треугольники”. В этом параграфе содержатся пункты “Окружность”, “Построения циркулем и линейкой” и “Примеры задач на построение”. Основываясь на том, что учащиеся умеют с 5 и 6 класса выполнять основные построения с помощью циркуля и линейки, в теме рассматриваются задачи на построение такие как: построение отрезка, равного данному; построение угла, равного данному; построение биссектрисы угла, перпендикулярных прямых и середины отрезка. Схема, по которой решаются задачи на построение, не вводится. Основная цель главы 2 – отработать навыки решения простейших задач на построение с помощью циркуля и линейки (см. Приложение 1).
В главе 3 “Параллельные прямые” рассматривается построение параллельных прямых с помощью чертежного треугольника и линейки, а также с помощью циркуля и линейки по заданной прямой и точке (в форме задачи).
В главе 4 “Соотношения между сторонами и углами треугольника” рассматривается задача о построении треугольника по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам и по трем сторонам. Данная глава содержит целый блок задач на построение для самостоятельного решения, который состоит в основном из задач на построение различных треугольников по различным элементам.
В конце 7 класса также имеется блок задач на построение, перед которым описывается схема, по которой решают задачи на построение: анализ, построение, доказательство, исследование. Приводится пример.
б) 8 класс: содержит пять глав. В главе 5 “Четырехугольники” после изучения многоугольника, параллелограмма и трапеции вводится блок задач на построение параллелограмма и трапеции по различным элементам. Перед этим еще раз идет повторение схемы решения задач на построение. В этой же главе после изучения прямоугольника, ромба и квадрата предлагается решить задачи на их построение.
В главе 7 “Подобные треугольники” рассматриваются задача на построение треугольника, при решении которой применяется метод подобия (в данном случае треугольников), в качестве практического приложения подобия треугольников. Также приводится ряд задач на построение треугольников по данным отношениям для самостоятельного решения. Основная цель главы 7 – сформировать понятие подобных треугольников, выработать умение применять признаки подобия треугольников, сформировать аппарат решения прямоугольных треугольников (см. Приложение 1).
В начале главы 8 “Окружность” в пункте “Касательная к окружности” решается задача о проведении касательной к окружности через данную точку. Говорится о том, что решение подобных задач основано на теореме (признаке касательной). Также в главе изучаются четыре замечательные точки треугольника. Задачи на построение (касательной к окружности, серединного перпендикуляра к отрезку) содержит каждый пункт главы. Основная цель главы 8 – дать учащимся систематизированные сведения об окружности и ее свойствах, вписанной и описанной окружностях (см. Приложение 1).
В конце 8 класса в разделе задач повышенной трудности встречается задача на построение равнобедренной трапеции по основаниям и диагоналям. А также построения встречаются в задачах на повторение.
в) 9 класс: содержит четыре главы. В главе 12 “Длина окружности и площадь круга” в §1 “Правильные многоугольники” рассматривается построение правильных многоугольников. Предлагается с помощью циркуля и линейки вписать в окружность различные правильные многоугольники. Также построения встречаются в задачах не повторение. Основная цель главы 12 – расширить и систематизировать знания учащихся об окружностях и многоугольниках (см. Приложение 1).
В главе 13 “Движения” изучаются симметрии, поворот и параллельный перенос. В конце главы содержатся задачи на построение, решение которых основано на изученном материале. Основная цель главы 13 – познакомить с понятием движения на плоскости: симметриями, параллельным переносом, поворотом (см. Приложение 1).
2) А.В. Погорелов [5]
а) 7 класс: содержит пять параграфов. В §1 “Основные свойства простейших геометрических фигур” рассматривается, как построить параллельные прямые с помощью угольника и линейки. В §2 “Смежные и вертикальные углы” рассматривается, как построить перпендикулярные прямые с помощью угольника и линейки. §5 “Геометрические построения” содержит пункт “Что такое задачи на построение”, где рассказывается о чертежных инструментах и о том, что значит решить задачу на построение. Схема решения не вводится. В следующих пунктах рассматриваются задачи на построение треугольника с данными сторонами; угла, равного данному; биссектрисы угла; деление отрезка пополам; построение перпендикуляра к прямой. Далее идут пункты “Геометрическое место точек”, в котором вводится определение ГМТ и Теорема о ГМТ, равноудаленных от двух данных точек; а также “Метод геометрических мест”, который раскрывает сущность данного метода. В конце параграфа приводится ряд задач на построение для самостоятельного решения. В основном это задачи на построение треугольника и окружности по данным элементам и задачи на ГМТ. Основная цель §5 – решать простейшие задачи на построение с помощью циркуля и линейки (см. Приложение 1).
б) 8 класс: содержит пять параграфов. В конце §6 “Четырехугольники” содержится задача на построении четвертого пропорционального отрезка. Также содержится ряд задач на построение параллелограмма, ромба и трапеции по данным элементам. Основная цель §6 – дать учащимся систематизированные сведения о четырехугольниках и их свойствах (см. Приложение 1). В §9 “Движение” изучаются геометрические преобразования: центральная и осевая симметрии, поворот, параллельный перенос. В конце параграфа приведены задачи на построение, решение которых основано на методах данных преобразований. Основная цель §9 – познакомить учащихся с примерами геометрических преобразований (см. Приложение 1).
в) 9 класс: в §11 “Подобие фигур” изучаются геометрические преобразования: подобие и гомотетия. В конце параграфа приведены задачи на построение, решение которых основано на методах данных преобразований. Основная цель §11 – усвоить признаки подобия треугольников и отработать навыки их применения (см. Приложение 1). В §13 “Многоугольники” рассматриваются построения некоторых правильных многоугольников. В конце имеется пара задач: вписать в окружность n-угольник и описать около окружности правильный n-угольник. Основная цель §13 – расширить и систематизировать сведения о многоугольниках и окружностях (см. Приложение 1).
3) А.Д. Александров, А.Л. Вернер, В.И. Рыжик [6]
а) 7 класс: содержит три главы. В главе 1 “Начала геометрии” в §5 “Окружность и круг” содержится пункт “Построения циркулем и линейкой”, в котором рассказывается о чертежных инструментах, с помощью которых выполняются задачи на построение. Тут же приводится задача на построение треугольника, стороны которого равны сторонам данного треугольника. Приводится построение, доказательство и исследование, но на общей схеме внимание не заостряется. §6 “Углы” содержит пункт “Построение угла, равного данному, циркулем и линейкой”. Для самостоятельного решения задач нет. В §7 “Действия над углами” рассматривается задача на построение биссектрисы угла, которая решает еще две задачи: в данной точке прямой провести перпендикуляр к ней, построить прямой угол. Также параграф содержит пункт “Задача о делении угла на равные части циркулем и линейкой”, в котором рассказывается о неразрешимости задачи о трисекции угла. Основная цель главы 1 – рассказать о задачах систематического курса геометрии и заложить основу для его построения (см. Приложение 1).
В главе 2 “Треугольники” в §10 “Признаки равенства треугольников” рассматривается задача о построении треугольника по двум сторонам и углу между ними. В §11 “Серединный перпендикуляр” первыми пунктами идут задачи о делении отрезка пополам и о построении перпендикуляра к данной прямой через данную точку, не лежащую на данной прямой. В конце параграфа содержится несколько задач на построение. Основная цель главы 2 – развить навыки решения задач на построение с помощью циркуля и линейки, начать знакомство с симметриями фигур (см. Приложение 1).
В главе 3 “Параллельность” в §13 “Параллельные прямые” изучается, как строить параллельные прямые с помощью угольника и линейки. В §14 “Аксиома параллельности” рассматривается задача о построении треугольника по стороне и двум прилежащем к ней углам.
б) 8 класс: содержит три главы. В главе 5 “Метрические соотношения в треугольнике” в § “Применение теоремы Пифагора” содержится пункт “Геометрическое место точек”, где объясняется, что значит, когда про фигуру говорят, что она является ГМТ, обладающих данным свойством. Также приводятся примеры, каким ГМТ являются биссектриса и серединный перпендикуляр. Параграф содержит такие задачи как, например, найти ГМТ, равноудаленных от прямой на данное расстояние; найти ГМТ, равноудаленных от двух данных пересекающихся прямых.
в) 9 класс: содержит две главы. В главе 7 “Многоугольники и окружности” в задачах для самостоятельного решения к §31 “Хорды и касательные” содержатся задача на нахождение ГМТ, из которых данный отрезок виден под данным углом; задача на построение касательной к окружности из данной точки, общей касательной к двум окружностям. §33 “Правильные многоугольники” содержит пункт “Построение правильных многоугольников” с помощью циркуля и линейки. Также в нем рассказывается о том, что циркулем и линейкой могут быть построены не все правильные n-угольники, а только те, у которых n имеет определенное разложение. Предлагается решить задачи: вписать в окружность различные правильные n-угольники. В §35 “Площадь круга” рассказывается о неразрешимой задаче о квадратуре круга.
В главе 8 “Другие методы геометрии” в §36 “Метод координат” содержится пункт “Окружность Аполлония”, где решение задачи о ГМТ, отношение расстояний от которых до двух данных точек есть постоянная величина. В §40 “Виды движений” рассматриваются “Метод параллельного переноса”, “Метод симметрии” и “Метод поворота”. Приводятся примеры задач на построение, решение которых основано на данных методах. В задачах для самостоятельного решения к §40 содержатся задачи на отработку изученных методов, в том числе задачи на построение трапеции и треугольника по данным элементам. В §42 “Подобие” рассматривается “Метод подобия”. В качестве примера приводится задача на построение четвертого пропорционального отрезка. В задачах для самостоятельного решения к §42 содержатся задачи на отработку изученного метода, в том числе задачи на построение прямоугольного треугольника по отношению катетов к гипотенузе и по отношению катетов к периметру. А также задачи: построить квадрат, вписанный в треугольник, ромб, сегмент; построить сегмент, вписанный в равносторонний треугольник, квадрат, окружность. Основная цель главы 8 – познакомить учащихся с методами, отсутствовавшими в классической элементарной геометрии, но играющими в современной геометрии ведущую роль: методом координат, векторным методом, методом преобразований (см. Приложение 1).
4) А.П. Кисилев, Н.А. Рыбкин [8]
Учебник содержит пять глав и сборник задач по геометрии.
В главе 1 “Прямая линия” в §1 “Углы ” рассматривается построение перпендикулярных прямых с помощью угольника и линейки. §3 “Треугольники” содержит пункт “Геометрическое место”, где дается определение ГМТ, и приводятся примеры: что является ГМТ серединного перпендикуляра и биссектрисы. Далее следует § 4 “Основные задачи на построение”, где рассматриваются задачи на построение треугольника по трем его сторонам; угла, равного данному; биссектрисы угла; перпендикуляра к прямой из данной точки, лежащей и не лежащей на прямой; серединного перпендикуляра; задача о делении отрезка пополам; построение треугольника по основанию, углу, прилежащему к основанию, и сумме двух боковых сторон. После рассмотренных задач приводится схема решения задач на построение: анализ, построение, доказательство, исследование. В конце §4 имеется блок задач на построение для самостоятельного решения, который содержит задачи на построение суммы, разности углов; деление угла на n частей; построение различных треугольников по различным элементам; разделение данного отрезка на n равных частей; задачи на нахождение ГМТ, равноудаленных от двух данных точек, от трех вершин треугольника, от трех сторон треугольника и т.д. В §5 “Параллельные прямые” рассматривается построение параллельных прямых с помощью угольника и линейки. §6 “Параллелограммы и трапеции” содержит пункт “Задачи на построение”, в котором рассматриваются методы параллельного переноса, симметрии и примеры задач. Также учащимся предлагается самостоятельно решить задачи на построение трапеций, четырехугольников и треугольников по различным данным элементам, основываясь на изученных методах. В конце главы 1 имеется ряд задач на нахождение ГМТ и блок задач на построение.
В главе 3 “Подобные фигуры” в §4 “Подобие фигур произвольного вида” имеется пункт “Задачи на построение”, в котором рассматривается метод подобия, но задач на применение метода данный пункт не содержит. В §5 “Некоторые теоремы о пропорциональных отрезках” рассматривается задача о построении четвертого пропорционального отрезка. В §6 “Метрические соотношения между элементами треугольника и некоторых других фигур” рассматривается задача о построении отрезка, среднего пропорционального между двумя данными отрезками. §8 “Тригонометрические функции острого угла” содержит пункт “Построение угла по заданной величине одной из его тригонометрических функций”. В §9 “Понятие о приложении алгебры к геометрии” рассматривается задача о разделении отрезка в среднем и крайнем отношении, а затем следует пункт “Алгебраический способ решения геометрических задач”, который раскрывает алгебраический метод решения задач на построение. Следующим пунктом идет “Построение простейших формул” с помощью циркуля и линейки. В конце главы 3 содержится ряд задач на нахождение ГМТ и блок задач на построение.
В главе 4 “Правильные многоугольники” в §1 “Правильные многоугольники” рассматривается задача: вписать в данный круг правильный десятиугольник и определить его сторону в зависимости от радиуса. Также далее в пункте “На сколько равных частей можно делить окружность с помощью циркуля и линейки?”, в котором дается указание, как разделить окружность на определенное равное количество частей (и вписать в окружность правильные многоугольники с таким числом сторон).
В главе 5 “Измерение площадей” в §1 “Площади многоугольников” рассматриваются задачи на построение треугольника (квадрата), равновеликого данному; квадрата, площадь которого равна сумме (разности) площадей двух данных квадратов; площадь которого относится к площади данного квадрата, как m:n; разделить данный треугольник на m равновеликих частей прямыми, параллельными его стороне. В §2 “Площадь круга и его частей” приводится пункт, в котором рассказывается о неразрешимой задаче о квадратуре круга. В конце главы 5 содержится блок задач на построение.
В сборнике задач также имеются задачи на построение.
Вывод: В учебниках для 5-6 классов задачи на построение практически не рассматриваются как самостоятельные. Чаще всего это задания на построение фигур по заданным размерам. Процент заданий на построение из всех геометрических заданий: 5 класс – 39%, 6 класс – 34%. В целом картина кажется достаточно отрадной. Однако если учесть, что сам по себе геометрический материал в учебниках не превышает 13-16% от всего содержания учебника, то указанный процент заданий на построение падает до 4-6% [3].
Во всех учебниках по геометрии для 7-9 класса задачи на построение рассматриваются как самостоятельные в конце 7 класса. Осуществляются следующие элементарные построения: деление отрезка пополам; откладывание угла, равного данному; построение биссектрисы угла; построение перпендикуляра к прямой из данной точки, не лежащей на этой прямой. В качестве метода решения задач на построение в учебниках (кроме учебника [7]) рассматривается метод геометрического места точек. Схема решения приводится в учебниках [7], [8]. В учебнике [6] схема приводится без анализа. В учебнике [5] ее нет.
В 8-9 классах встречаются задания на построение фигур по некоторым заданным элементам. Произвольные треугольники и четырехугольники строятся по сторонам и углам. Четырехугольники особых видов (ромбы, квадраты, прямоугольники) – по сторонам и диагоналям. Рассматриваются приемы описывания и вписывания окружностей в треугольники и четырехугольники.
Алгебраический метод решения задач на построение приводится только в учебнике [8]. В учебнике [6] рассказывается о трисекции угла, квадратуре круга, окружности Аполлония.
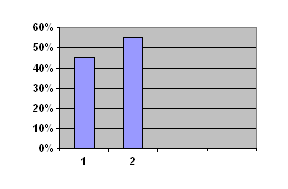
В таблице приведен количественный анализ (процент заданий на построение) в учебниках:
| Учебники | Класс | Всего задач в учебнике | Из них на построение | Процент от общего числа задач |
| Александров А.Д. и др. “Геометрия 7-9” | 7 | 33 | 8 | 24 |
| 8 | 643 | 95 | 15 | |
| 9 | 556 | 89 | 16 | |
| Атанасян Л.С. и др. “Геометрия 7-9” | 7 | 362 | 90 | 25 |
| 8 | 448 | 64 | 14 | |
| 9 | 321 | 36 | 11 | |
| Погорелов А.В. “Геометрия 7-9” | 7 | 218 | 42 | 20 |
| 8 | 298 | 35 | 12 | |
| 9 | 206 | 10 | 5 |
Рассматривая учебники, можно отметить, что в них достаточно высок процент заданий на построение в 7 классе, причем рассматриваются стандартные и элементарные задачи на построение. Однако к 9 классу процент геометрических заданий на построение резко падает. Быть может ситуация обусловлена тем, что к 9 классу у всех школьников уже развито логическое и пространственное мышление, сформированы графические умения и навыки, они легко и верно читают любой чертеж, не затрудняются с его интерпретацией, легко строят любой нужный чертеж по тексту задачи? Увы, ситуация совсем не такова. Так как задания на построение составляют базу для работы, развивающей навыки построения фигур, способствующей формированию умения читать и понимать чертеж, устанавливать связи между его частями, то недостаточность этой системы обусловливает плохое развитие пространственного и логического мышления ученика, низкий уровень его графической культуры. Эти недостатки не позволяют ученику эффективно изучать те разделы математики, где самостоятельно сделанная и хорошо понятая графическая интерпретация является тем самым “лучом света в темном царстве”, которого так иногда не хватает школьнику при изучении математики.
1.2 Анализ учебно-методической литературы
1) И.Ф. Шарыгин “Задачи по геометрии (Планиметрия)” [28]
Книга, состоящая из двух частей, включает более 600 задач по планиметрии. Вторая часть содержит параграф, посвященный теме геометрических мест точек. Задач предлагается немного, они достаточно сложные, предназначенные по большей мере для специализированных классов, для студентов. Задачи сопровождаются указаниями и подробными решениями. В некоторых других параграфах второй части, таких как, например, “Треугольник” и “Окружности и касательные”, также встречаются задачи на нахождение геометрического места точек.
2) В.В. Прасолов “Задачи по планиметрии (в двух частях)” [22] [23]
В этот сборник включены нестандартные геометрические задачи несколько повышенного по сравнению со школьными знаниями уровня. Для всех задач прилагаются решения. Книга состоит из двух частей. Первая содержит классические темы планиметрии, вторая – геометрические преобразования и задачи на олимпиадную и кружковую тематику.
Всего 29 глав. За основу классификации задач приняты методы решения геометрических задач. Одна из глав посвящена методу ГМТ, которая содержит достаточное количество задач на построение разного уровня сложности, в которых применяется данный метод. Применяются как основные ГМТ, так и более сложные.
Есть глава, посвященная геометрическим построениям треугольников, четырехугольников, окружностей с помощью различных методов, включает в себя разнообразный набор задач на построение. Кроме того, в этой главе рассматриваются построения с помощью одной линейки, одной двусторонней линейки, с помощью одного прямого угла. Также здесь приводятся необычные построения (например, деление угла на n равных частей).
Имеются отдельные главы, посвященные методам параллельного переноса, центральной симметрии, осевой симметрии, поворота, гомотетии, в которых также хорошо отражена суть методов и содержится хороший набор задач разного уровня на применение каждого метода. Даются основные понятия к каждой главе.
3) Я.П. Понарин “Элементарная геометрия (в двух томах)” [20] [21]
Книга предназначена для более углубленного изучения элементарной геометрии. Для учащихся школ, лицеев, гимназий с математической специализацией и студентов. Первый том посвящен планиметрии и преобразованиям плоскости, второй – стереометрии и преобразованиям пространства.
В данном пособии уделено много внимания методу геометрических преобразований, в связи с тем, что чисто геометрические методы в последнее время отходят на второй план и данный метод до сих пор не нашел своего места в школьном курсе геометрии. Как пишет автор, его пытались изучать с самого начала, растянув на всю восьмилетнюю школу. Теперь предполагается заняться им в конце изучения планиметрии. Но по-прежнему ученики не владеют им даже на начальном уровне. В книге расширен материал школьных учебников, добавлены многие геометрические факты. Теория геометрических построений вынесена за рамки пособия. В систематическом виде изложен теоретический и задачный материал по методу геометрических преобразований плоскости. Он позволяет оригинально и красиво решать многие геометрические задачи. Большую часть пособия составляют задачи различной степени трудности, к большинству из них даны ответы или краткие указания.
Первый том содержит две части. Вторая часть посвящена преобразованиям плоскости. В частности две первые ее главы описывают движения плоскости и методы решения задач на построение (центральная симметрия, осевая симметрия, параллельный перенос, поворот, подобие).
Второй том также содержит две части. В первой части четвертая глава посвящена ГМТ. Здесь рассматриваются различные ГМТ плоскости, а также ГМТ пространства: разность квадратов расстояний, сумма квадратов расстояний, сфера Аполлония. Применение метода ГМТ для решения стереометрических задач. Вторая часть посвящена преобразованиям пространства аналогично второй части первого тома. Две первые ее главы описывают движения пространства и методы решения задач на построение (центральная симметрия, осевая симметрия, параллельный перенос, поворот, подобие).
В книге отдельно не выделяется применение метода ГМТ для планиметрических задач, а также не рассмотрен алгебраический метод.
4) И.И. Александров “Сборник геометрических задач на построение с решениями” [1]
Книга насчитывает более 600 задач на построение, что представляет учащимся и преподавателям огромный выбор. В основном книга посвящена решению задач на построение при помощи циркуля и линейки, но последний раздел посвящен решению задач одним циркулем, двусторонней линейкой, прямого или острого угла, односторонней линейкой с применением вспомогательной окружности Штейнера.
Сборник можно разделить на три части, включающие: 1) основные построения; 2) задачи, приучающие к построениям; 3) задачи на различные методы решения (метод ГМТ, метод геометрических преобразований, алгебраический метод). Представлен очень хороший набор задач различной степени сложности, на применение различных методов, и приведены решения. Каждый метод подробно описан, приведены примеры. Также в книге рассмотрена тема: “Применение тригонометрии к решению геометрических задач на построение”.
Вывод: Во всех книгах достаточно хорошо рассмотрены те или иные методы решения задач на построение, приведены решения задач. В книге [28] представлены задачи только на метод ГМТ. Сборники [22], [23] содержат отдельные главы, посвященные различным методам (кроме алгебраического). Включенные в них задачи имеют несколько повышенный по сравнению со школьными знаниями уровень. Наиболее оптимальным из рассмотренных книг, по нашему мнению, является сборник [1], он содержит много задач на применение различных методов. Причем только в нем рассматривается алгебраический метод. Кроме того, достаточно хорошими книгами являются пособия [20], [21]. В них наилучшим образом представлена тема геометрических преобразований и только здесь рассматривается ГМТ пространства.2. Логическое мышление: основные понятия. Анализ психолого-педагогической литературы 2.1 Природа и виды мышления
Существуют различные подходы к понятию “мышление”. Приведем некоторые из них.
Мышление – высшая форма активного отражения объективной реальности, состоящая в целенаправленном, опосредованном и обобщенном познании субъектом существующих связей и отношений предметов и явлений в творческом созидании новых идей, в прогнозировании событий и явлений [27].
Мышление – социально обусловленный, неразрывно связанный с речью психический процесс поисков и открытия существенно нового, процесс опосредованного и обобщенного отражения действительности в ходе ее анализа и синтеза. Мышление возникает на основе практической деятельности из чувственного познания и далеко выходит за его пределы [16].
Мышление отражает бытие в его связях и отношениях, в его многообразных опосредованиях.
Мышление — это обобщенное отражение объективной действительности в ее закономерных, наиболее существенных связях и отношениях. Оно характеризуется общностью и единством с речью. Другими словами, мышление есть психический процесс познания, связанный с открытием субъективно нового знания, с решением задач, с творческим преобразованием действительности.
Мышление – психический процесс обобщенного и опосредованного отражения устойчивых, закономерных свойств и отношений действительности, существенных для решения познавательных проблем, схематической ориентации в конкретной ситуациях.
Выделяют следующие виды мышления [26]:
1) Наглядно-действенное мышление. Основная характеристика этого мышления: решение задачи осуществляется с помощью реального преобразования ситуации, с помощью наблюдаемого двигательного акта.
2) Образное (или наглядно-образное) мышление. Функции образного мышления связаны с представлением ситуаций и изменений в них, которые человек хочет получить в результате своей деятельности, преобразующей ситуацию; с конкретизацией общих положений. С помощью образного мышления более полно воссоздается все многообразие различных фактических характеристик предмета. В образе может быть зафиксировано одновременное видение предмета с нескольких точек зрения. Очень важная особенность образного мышления — установление непривычных, “невероятных” сочетаний предметов и их свойств. В отличие от наглядно-действенного мышления при наглядно-образном мышлении ситуация преобразуется лишь в плане образа.
3) Теоретическое (или словесно-логическое) мышление. Это мышление характеризуется использованием понятий, логических конструкций, существующих, функционирующих на базе языка, языковых средств. Теоретическое мышление выявляет всеобщее отношение, исследует объект познания в системе его необходимых связей. Его результат – построение теоретических моделей, создание теорий, обобщение опыта, раскрытие закономерности развития различных явлений, знание которых обеспечивает преобразовательную деятельность человека. Теоретическое мышление неразрывно связано с практикой, но в своих конечных результатах имеет относительную самостоятельность.
Описанная классификация (тройка) не является единственной. В психологической литературе используется несколько “парных” классификаций [26]:
1) Теоретическое и практическое мышление по типу решаемых задач и вытекающих отсюда структурных и динамических особенностей. Теоретическое мышление — это познание законов, правил. Основная задача практического мышления — подготовка физического преобразования действительности: постановка цели, создание плана, проекта, схемы. Одна из важных особенностей практического мышления заключается в том, что оно развертывается в условиях жесткого дефицита времени. В практическом мышлении очень ограниченные возможности для проверки гипотез. Все это делает практическое мышление подчас еще более сложным, чем мышление теоретическое. Теоретическое мышление иногда сравнивают с мышлением эмпирическим. Здесь в качестве критерия используется характер обобщений, с которыми имеет дело мышление: в одном случае это научные понятия, а в другом — житейские, ситуативные обобщения.
2) Интуитивное и аналитическое (логическое) мышление. Обычно используются три признака: временной (время протекания процесса), структурный (членение на этапы), уровень протекания (осознанность или неосознанность). Аналитическое (логическое) мышление развернуто во времени, имеет четко выраженные этапы, в значительной степени представлено в сознании самого мыслящего человека. Интуитивное мышление характеризуется быстротой протекания, отсутствием четко выраженных этапов, является минимально осознанным.
3) Реалистическое и артистическое мышление. Реалистическое мышление направлено в основном на внешний мир, регулируется логическими законами. Артистическое мышление связано с реализацией желаний человека. Иногда используется термин эгоцентрическое мышление, оно характеризуется, прежде всего, невозможностью принять точку зрения другого человека.
4) Продуктивное и репродуктивное мышление. Различие основано на степени новизны получаемого в процессе мыслительной деятельности продукта по отношению к знаниям субъекта.
Сравнительная таблица основных видов мышления (см. Приложение 2).
2.2 Развитие мышления ребенка
В преддошкольном возрасте (до трех лет включительно) мышление в основном наглядно-действенное.
В возрасте четырех – семи лет возникает наглядно-образное мышление в простейшей форме преимущественно у дошкольников. Дошкольники мыслят лишь наглядными образами и еще не владеют понятиями (в строгом смысле) [17].
В школьном возрасте в процессе систематического мышление ребенка начинает перестраиваться и развивается теоретическое мышление.
По мере формирования теоретического мышления ребенок, подросток все больше учится осознавать обобщенные закономерности явлений. Ребенок не столько все глубже познает действительность, по мере того как развивается его мышление, сколько его мышление все более развивается, по мере того как углубляется его познавательное проникновение в действительность.
С 11 до 14 лет резко возрастает значимость причинных связей в мышлении ребенка, причем сначала сильно преобладает интерес к причинам явлений. Затем соотношение изменяется: подростка начинает больше интересовать будущее, его мышление начинает направляться на раскрытие следствий. Вместе с тем от установления единичных причинно-следственных зависимостей в частных наглядных ситуациях оно поднимается к пониманию общих закономерностей.
Новый уровень отвлеченной теоретической мысли сказывается также во взаимоотношениях мышления и речи, а также мышления и наглядно-образного содержания восприятия, представления.
В отношении между мышлением и речью новый уровень мышления находит себе выражение в том, что: а) значительную роль в речи начинают играть термины; б) другим выражением того же сдвига в мышлении является развивающееся в этот период понимание метафорического переносного значения слов; в) особенно заостренно сказываются особенности речевой формы отвлеченного мышления в умении оперировать формулами с буквенными обозначениями (алгебра, логика).
Развитие мышления ребенка происходит поэтапно, представляет собой некоторые ступени развития. При этом высшие ступени, развиваясь, не вытесняют низших, а преобразуют их. Когда развивается теоретическое мышление, то ни наглядно-действенное, ни наглядно-образное мышление, конечно, не исчезают, а преобразуются, совершенствуются, сами поднимаются на высшую ступень. Между ними создаются многообразнейшие, сложные, от случая к случаю индивидуально варьирующиеся взаимоотношения.
На различных этапах развития мышления разные области знания являются той базой, на которых формируются более высокие формы мышления, на которых оно раньше всего переходит на высшую ступень. В раннем возрасте такой областью является арифметика. При переходе из начальной в среднюю школу такую же роль в развитии отвлеченного мышления может играть алгебра. В разные периоды разные науки вносят каждая свой специфический вклад в развитие мышления и могут явиться тем плацдармом, на котором раньше формируются те или иные стороны более высоких ступеней мышления [24].
2.3 Понятие логического мышленияЛогическое мышление как феномен изучается различными науками: философией, психологией, логикой. Каждая из них по-своему, что вполне справедливо, определяет его сущность.
Так, например, в одних источниках логическим мышлением называют процесс мышления, в котором умозаключения строго основываются на правильных суждениях. При таком мышлении явление получает убедительное объяснение, безошибочно устанавливаются причины и следствия, выявляются связи и отношения между понятиями, которые выражаются в суждениях, верность которых нельзя опровергнуть.
В других – определяют словесно-логическое мышление как один из видов мышления, характеризующийся использованием понятий, логических конструкций.
В свою очередь, в словаре психологических понятий К.К. Платонова логическое мышление определяется как “вид мышления, сущность которого в ориентировании понятиями, суждениями и умозаключениями с использованием законов логики” [19].
Отметим, что в психолого-педагогической литературе “логическое мышление” практически отождествляется с понятием “абстрактное”, “теоретическое”, “понятийное”, “категориальное”, “словесно-логическое (дискурсивное)” мышление, иногда они рассматриваются как синонимы.
Но при этом все сходятся в том, что логическое мышление – есть абстрактное, аналитическое, синтетическое мышление, функционирующее на базе языковых средств, активно развивающееся у человека, начиная с определенного возраста – с началом его обучения.
Цель развития логического мышления (определенность, последовательность, доказательность мысли) достигается решением следующих задач: овладение основными мыслительными операциями, структурой логических форм мышления, переносом приемов мыслительной деятельности из одной области знаний в другую. Организация логической подготовки базируется на принципах преемственности, учета возрастных особенностей, раскрытия общезначимости логических форм и отношений и др.; а содержание ее включает основные логические умения и соответствующие им мыслительные операции. Развитие логического мышления осуществляется посредством изучения процесса мышления, активного использования речи, соединения и взаимообогащения всех видов мышления.
2.4 Развитие логического мышления школьников в процессе обучения математике
Отметим, что развитие логического мышления непосредственно связано с процессом обучения математике. При этом многие исследователи отмечают, что одной из важнейших задач обучения, в том числе и математике, в школе является формирование у учащихся навыков осуществления логических операций, обучение их различным приемам логического мышления, вооружение знаниями логики и выработки у школьников умений и навыков использования этих знаний в учебной и практической деятельности.
В результате правильно организованного обучения математике школьники весьма быстро приобретают навыки логического мышления, в частности, умение обобщать, классифицировать и аргументированно обосновывать свои выводы.
Вместе с тем нет единого подхода к решению вопроса, как организовать такое обучение математике. Одни считают, что логические приемы являются неотъемлемой частью математики как науки, основы которой включены в содержание образования, поэтому у учащихся при изучении математики автоматически развивается логическое мышление на основе заданных образов (В.Г. Бейлинсон, Н.Н. Поспелов, М.Н. Скаткин).
Другой подход выражается во мнении части исследователей о том, что развитие логического мышления только через изучение учебных предметов, в том числе и математики, является малоэффективным, такой подход не обеспечивает полноценного усвоения приемов логического мышления и поэтому необходимы специальные учебные курсы по логике (Ю.И. Веринг, Н.И. Лифинцева, В.С. Нургалиев, В.Ф. Паламарчук).
Еще одна группа ученых (Д.Д. Зуев, В.В. Краевский) считают, что развитие логического мышления учащихся должно осуществляться на конкретном предметном содержании учебных дисциплин через акцентуацию, выявление и разъяснение встречающихся в них логических операций.
Но каков бы ни был подход к решению этого вопроса, большинство исследователей сходятся в том, что развивать логическое мышление в процессе обучения математике это значит: развивать у учащихся умение сравнивать наблюдаемые предметы, находить в них общие свойства и различия; вырабатывать умение выделять существенные свойства предметов и отвлекать (абстрагировать) их от второстепенных, несущественных; учить детей расчленять (анализировать) предмет на составные части в целях познания каждой составной части и соединять (синтезировать) расчлененные мысленно предметы в одно целое, познавая при этом взаимодействие частей и предмет как единое целое; учить школьников делать правильные выводы из наблюдений или фактов, уметь проверять эти выводы; прививать умение обобщать факты; развивать у учащихся умение убедительно доказывать истинность своих суждений и опровергать ложные умозаключения; следить за тем, чтобы мысли учащихся излагались определенно, последовательно, непротиворечиво, обоснованно.
Решение задач на построение, несомненно, развивает логическое и активное мышление учащихся. Ни одни задачи не содействуют так развитию в учениках наблюдательности и правильности мышления, представляя в то же время для них и наибольшую привлекательность, как геометрические (задачи) на построение.
Большое значение для развития логического мышления учащихся имеют и задачи на построение. Наличие анализа, доказательства и исследования при решении большинства таких задач показывает, что они представляют собой богатый материал для выработки у учащихся навыков правильно мыслить и логически рассуждать. При решении задач на построение они имеют дело не с конкретной, определенной фигурой, а должны создать необходимую фигуру, подвергающуюся различным изменениям в процессе решения. Вскрывая взаимосвязи между данными элементами, видим, как с изменением одних изменяются другие и даже вся фигура. Этим мы приучаем учащихся к диалектическому методу мышления и по возможности устраняем формализм в знаниях.
Трудно переоценить роль задач на построение в математическом развитии школьников. Они по своей постановке и методам решения не только наилучшим образом стимулируют накопление конкретных геометрических представлений, но и развивают способность отчетливо представлять себе ту или иную геометрическую фигуру и, более того, уметь мысленно оперировать элементами этой фигуры. Задачи на построение могут способствовать пониманию учащимися происхождения различных геометрических фигур, возможности их преобразования – все это является важной предпосылкой развития пространственного мышления школьников. Они сильно развивают логическое мышление, геометрическую интуицию.
Между тем заметим, что процесс формирования логического мышления, общелогических умений, как компонента общего образования, должен быть целенаправленным, непрерывным и связанным с процессом обучения математике на всех ее ступенях.
Вывод: Логическое мышление – есть абстрактное, аналитическое, синтетическое мышление, функционирующее на базе языковых средств, активно развивающееся у человека, начиная с определенного возраста – с началом его обучения. Развитие логического мышления – это формирование у учащихся навыков осуществления логических операций, обучение их различным приемам логического мышления, вооружение знаниями логики и выработка умений и навыков использования этих знаний в учебной и практической деятельности. Этот процесс непосредственно связан с процессом обучения математике, правильная организация которого обеспечивает наиболее эффективное развитие логического мышления, в том числе и при решении геометрических задач. При этом ни одни задачи не содействуют так развитию в учениках наблюдательности и логического мышления, представляя в то же время для них и наибольшую привлекательность, как задачи на построение.
3. Методика решения задач на построение
Суть решения задачи на построение состоит в том, что требуется построить наперед указанными инструментами некоторую фигуру, если дана некоторая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры.
Каждая фигура, удовлетворяющая условиям задачи, называется решением этой задачи.
Найти решение задачи на построение – значит свести ее к конечному числу основных построений, то есть указать конечную последовательность основных построений, после выполнения которых, искомая фигура будет уже считаться построенной в силу принятых аксиом конструктивной геометрии.
Одной из основных проблем методики обучения решению задач на построение является методика введения и изучения этапов решения конструктивных задач. Еще в IV в. до н. э. древнегреческие геометры разработали общую схему решения задач на построение, которой мы пользуемся и теперь. Процесс решения задачи разбивают на 4 этапа: анализ, построение, доказательство и исследование. Рассмотрим каждый этап более подробно.
3.1 АнализАнализ — это важный этап решения задачи, который мы понимаем как поиск способа решения задачи на построение. На этом этапе должны быть подмечены такие зависимости между данными фигурами и искомой фигурой, которые позволили бы в дальнейшем построить эту искомую фигуру (если мы знаем, как строить искомую фигуру, то никакой анализ уже не нужен).
Анализ – подготовительный, предварительный этап решения задачи на построение.
Чтобы облегчить себе поиск связей между искомой фигурой и данными фигурами, обычно оказывается выгодным иметь перед глазами вспомогательный чертеж, чертеж-набросок, изображающий данные и искомые фигуры примерно в том расположении, которое предусмотрено условием задачи. Чертеж можно выполнить от руки, на глаз – это проект чертежа, который должен образоваться, когда задача уже решена.
На вспомогательном чертеже следует выделить данные элементы и важнейшие искомые элементы. Практически часто удобнее начинать построение вспомогательного чертежа не с данной фигуры, а с примерного изображения исходной фигуры, пристраивая к ней данные так, чтобы они находились в отношениях, указанны в условии задачи.
Если вспомогательный чертеж не подсказывает способа построения искомой фигуры, то пытаются обнаружить какую-либо часть искомой фигуры или вообще некоторую фигуру, которая может быть построена, и которой затем можно воспользоваться для построения искомой фигуры.
Также надо учитывать следующие моменты [2]:
1) если на вспомогательном чертеже не удается непосредственно заметить необходимые для решения связи между данными и искомыми элементами, то целесообразно ввести в чертеж вспомогательные фигуры: соединить уже имеющиеся точки прямыми, отметить точки пересечения имеющихся линий, продолжить некоторые отрезки и т. д. Иногда бывает полезно проводить параллели или перпендикуляры к уже имеющимся прямым;
2) если по условию задачи дана сумма или разность отрезков или углов, то эти величины следует ввести в чертеж, то есть следует изобразить их на чертеже-наброске, если их еще нет на нем;
3) в процессе проведения анализа бывает полезно вспомнить теоремы и ранее решенные задачи, в которых встречаются зависимости между элементами, о которых говорится в условии рассматриваемой задачи.
В Приложении 3 приведен анализ задачи на построение: “Построить треугольник, зная основание, меньший угол при основании и разность двух других сторон”.
Из данного примера видно, что при отыскании решения задачи на построение, как и для арифметических задач, применяется аналитико-синтетический метод. Следуя от вопроса задачи, учитываем, какие элементы нам известны, и, наоборот, исходные данные комбинируем так, чтобы построить искомую фигуру.
Название этапа “анализ” не означает, что для отыскания решения применяется только аналитический метод, подобно тому, как и при доказательстве, которое иногда называют “синтезом”, не всегда применяется синтетический метод рассуждения. При разборе задачи, при отыскании путей ее решения анализ и синтез находятся в постоянном взаимодействии, дополняют и проверяют друг друга.
3.2 ПостроениеВторой этап решения задач на построение состоит из двух частей:
1) перечисление в определенном порядке всех элементарных построений, которые нужно выполнить, согласно анализу, для решения задачи;
2) непосредственное выполнение этих построений на чертеже при помощи чертежных инструментов. Действительно, решить задачу с помощью тех или иных инструментов — значит указать конечную совокупность элементарных, допустимых для данных инструментов, построений, выполнение которых в определенной последовательности позволяет дать ответ на вопрос задачи.
Данный этап вводится при решении самой первой задачи на построение, которой обычно является задача о построении отрезка, равного данному, на данном луче с концом в начале этого луча. В беседе, сопровождающей введение этапа, необходимо отметить, в чем состоит решение любой задачи на построение и указать, что осуществление этого этапа как раз и состоит в перечислении конечного числа операций построения искомой фигуры.
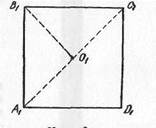
Рис. 1
Рассмотрим решение задачи: “Построить квадрат по его диагонали”.
Анализ. Проведя диагональ А1С1 (рис. 1), мы видим, что построение квадрата сводится к построению равнобедренного прямоугольного треугольника А1В1С1 по его гипотенузе A1C1, который затем легко дополнить до квадрата.
Построение. Треугольник А1В1С1 можно строить различными способами. Например:
1) Строим угол B1A1C1, содержащий 45°, и на одной его стороне откладываем отрезок А1С1, и равный данной диагонали. Проведя C1B1![]() A1B1, получим треугольник А1В1С1, который дополняем до квадрата A1B1C1D1, что можно сделать различными способами.
A1B1, получим треугольник А1В1С1, который дополняем до квадрата A1B1C1D1, что можно сделать различными способами.
2) Проведем через середину А1С1 перпендикуляр В1О1![]() А1С1и отложим B1O1=A1O1 и соединим В1 с А1 и С1; получим треугольник A1B1C1.
А1С1и отложим B1O1=A1O1 и соединим В1 с А1 и С1; получим треугольник A1B1C1.
3) На А1С1, как на диаметре, строим окружность и из точки О1 восставляем перпендикуляр О1В1![]() А1С1 до пересечения с окружностью в точке B1. Соединив В1 с А1 и С1, получим треугольник A1B1C1. Проведя B1D1
А1С1 до пересечения с окружностью в точке B1. Соединив В1 с А1 и С1, получим треугольник A1B1C1. Проведя B1D1![]() A1C1, мы сразу можем получить точки B1 и D1, как и в предыдущем случае. Очевидно, что построение треугольника A1B1C1 возможно и другими способами [11].
A1C1, мы сразу можем получить точки B1 и D1, как и в предыдущем случае. Очевидно, что построение треугольника A1B1C1 возможно и другими способами [11].
Решение одной и той же задачи несколькими способами усиливает интерес учащихся к задачам на построение и сознательное отношение к решению таких задач. Если решать задачи на построение все время по заранее указанным методам, то этим самым сковывается изобретательность и инициатива учащихся в нахождении различных и оригинальных способов решения и им трудно научиться самостоятельно решать конструктивные задачи. Они применяют в первую очередь знания изучаемого материала и навыки, полученные при решении задач, предшествующих данной. Если решались задачи, требующие применения определенного метода, то и для предложенной задачи они изберут тот же знакомый им путь решения, даже если он нерационален. Указание учителя на существование более простого способа не дает должного эффекта, так как предложенное учителем решение кажется учащимся искусственным, которого они сами не смогли бы найти.
Конечно, если это делать до того как ученики приобретут прочные навыки в отыскании решений различными способами, то результаты окажутся отрицательными. Внимание учащихся каждый раз будет распыляться между всеми способами, и они ни одного из них не усвоят основательно, чтобы применять его достаточно сознательно.
Различными способами хорошо решать задачи в конце учебного года, при повторении курса геометрии, когда учащиеся уже имеют достаточные навыки в решении задач на построение. Задачу, допускающую различные способы решения, лучше задавать на дом, чтобы они не только решили, но и нашли наиболее простое решение.
3.3 ДоказательствоПосле того как фигура построена, необходимо установить, удовлетворяет ли она условиям задачи, то есть показать, что фигура, полученная из данных элементов определенным построением, удовлетворяет всем условиям задачи. Значит, доказательство существенно зависит от способа построения. Одну и ту же задачу можно решать различными способами, в зависимости от намеченного при анализе плана построения, а поэтому, и доказательство в каждом случае будет свое. Доказательство представляет собой часть решения задачи, по своему логическому содержанию обратную анализу. Если в анализе устанавливается, что всякая фигура, удовлетворяющая поставленным условиям, может быть найдена таким-то и таким-то путем, то в этой, третьей части решения доказывается обратное положение. Это обратное положение в общем виде может быть сформулировано так: если некоторая фигура получена из данных элементов таким-то построением, то она действительно удовлетворяет поставленным условиям. В Приложении 3 приведено решение задачи: “Построить трапецию по четырем сторонам”.
При решении простейших задач, когда все условия задачи находят непосредственное отражение в плане построения, нет необходимости доказывать, что фигура, полученная из данных элементов таким построением, является искомой. Например: “Построить треугольник по двум сторонам и углу между ними”. Здесь доказательство сводится к простой проверке, такие ли взяли стороны, как данные, и будет ли построенный угол равен данному. В подобных задачах доказательство является излишним, ибо правильность решения обеспечивается соответствием построения анализу и данным условия задачи.
Доказательство не просто зависит от анализа и построения, между ними существует взаимосвязь и взаимообусловленность. Построение проводится по плану, составленному при анализе. Таких планов можно указать несколько. Построение и доказательство являются своеобразным критерием правильности и рациональности составленного плана. Если план не осуществим имеющимися инструментами или же построение оказывается нерациональным, мы вынуждены искать новый план решения. Аналогичным образом и доказательство, и исследование влияют на анализ, предопределяя нередко выбор плана решения.
Хотя доказательство при решении задач на построение проводится аналогично доказательству теорем, с использованием аксиом, теорем и свойств геометрических фигур, между ними имеется и некоторое различие. При доказательстве теорем в большинстве случаев без труда выделяют условие и заключение. При решении задач на построение уже труднее найти данные, на основании которых можно доказать, что построенная фигура является искомой. Поэтому при решении конструктивных задач в классе целесообразно иногда специально выделять, что дано, и что требуется доказать. Например, при решении задачи: “Построить ромб по двум его диагоналям” предлагаем ученику записать, что дано (диагонали взаимно перпендикулярны и, пересекаясь, делятся пополам) и что требуется доказать (стороны равны). В свою очередь при решении задач дома и в контрольных работах можно не требовать оформления доказательства с выделением отдельно условия и заключения. Нет надобности требовать проведения особого доказательства в задачах, где правильность решения очевидна [11].
3.4 ИсследованиеПри построении обычно ограничиваются отысканием одного какого-либо решения, причем предполагается, что все шаги построения действительно выполнимы. Для полного решения задачи нужно еще выяснить следующие вопросы: 1) всегда ли (то есть при любом ли выборе данных) можно выполнить построение избранным способом; 2) можно ли и как построить искомую фигуру, если избранный способ нельзя применить; 3) сколько решений имеет задача при каждом возможном выборе данных? Рассмотрение всех этих вопросов и составляет содержание исследования [2].
Таким образом, исследование имеет целью установить условия разрешимости и определить число решений. Нередко школьники и даже учителя проводят исследование, произвольно выбирая те или иные случаи, причем неясно, почему рассматриваются именно такие, а не какие-либо иные случаи. Остается неясным также, все ли возможные случаи рассмотрены. Практически в большинстве случаев удается достигнуть необходимой полноты исследования, если проводить это исследование по ходу построения, что является наиболее доступным и целесообразным способом. Сущность этого приема состоит в том, чтобы перебрать последовательно все шаги, из которых слагается построение, и относительно каждого шага установить, всегда ли указанное на этом шаге построение выполнимо, а если выполнимо, то однозначно ли.
Рассмотрим решение и исследование задачи: “Построить окружность, касающуюся данной прямой PQ и данной окружности (О; ОА) в заданной на ней точке А”.
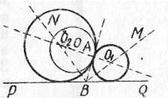
Рис. 2
Решение. Решаем эту задачу методом геометрических мест. Проводим прямую ОА (рис. 2). В точке А строим касательную АВ к данной окружности, а затем — биссектрисы углов РВА и ABQ. Точки пересечения прямой ОА с прямыми ВМ и BN и будут центрами искомых окружностей.
Проводя исследование по построению, легко обнаруживаем, что наше решение не применимо, если OA![]() PQ. Для такого случая рассматриваем решение задачи отдельно. В результате получим, что если ОА не перпендикулярна PQ, то задача имеет два решения, за исключением случая, когда окружность (О; ОА) пересекает PQ в точке А, так как тогда прямые ВМ, ВN и ОА пересекутся в точке А, и окружности не получим. Если же OA
PQ. Для такого случая рассматриваем решение задачи отдельно. В результате получим, что если ОА не перпендикулярна PQ, то задача имеет два решения, за исключением случая, когда окружность (О; ОА) пересекает PQ в точке А, так как тогда прямые ВМ, ВN и ОА пересекутся в точке А, и окружности не получим. Если же OA![]() PQ, но А не лежит на PQ, то получаем одну окружность с центром на ОА и радиусом, равным половине расстояния от точки А до данной прямой PQ. Если же при этом А лежит на PQ, то задача неопределенная.
PQ, но А не лежит на PQ, то получаем одну окружность с центром на ОА и радиусом, равным половине расстояния от точки А до данной прямой PQ. Если же при этом А лежит на PQ, то задача неопределенная.
Таким образом, для задачи имеются лишь 4 характерные конфигурации исходных данных:
1) ОА не перпендикулярна PQ и А не принадлежит PQ — 2 решения;
2) OA не перпендикулярна PQ и A принадлежит PQ — нет решений;
3) OA![]() PQ, но A не принадлежит PQ — 1 решение;
PQ, но A не принадлежит PQ — 1 решение;
4) OA![]() PQ и А принадлежит PQ — бесконечное множество решений [11].
PQ и А принадлежит PQ — бесконечное множество решений [11].
В итоге таких рассуждений решается вопрос о возможности и однозначности построения искомой фигуры данным способом. Но остается еще открытым вопрос: не возникнут ли новые решения, если изменить как-либо способ построения? Иногда удается доказать, что всякое решение данной задачи совпадает с одним из уже полученных решений. Если же это не удается, то можно предположить, что задача имеет другие решения, которые могут быть найдены другими способами. В этих случаях надо тщательно проверить, нет ли каких-либо иных возможных случаев расположения данных или искомых фигур, которые не были предусмотрены ранее проведенным анализом.
Похожие работы
... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...
... координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных изображений. Можно выделить следующие цели изучения метода координат в школьном курсе геометрии: - дать учащимся эффективный метод решения задач и доказательства ряда теорем; - показать на основе этого метода тесную связь алгебры и геометрии; - способствовать ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
... Таким образом, в современном мире необходимы информационно-коммуникационные технологии. ГЛАВА II. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ ПО ТЕМЕ: «ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ КАК СРЕДСТВО РАЗВИТИЯ ПОЗНАВАТЕЛЬНОГО ИНТЕРЕСА ПРИ ИЗУЧЕНИИ ЖИВОТНОГО МИРА В НАЧАЛЬНОЙ ШКОЛЕ» 2.1 Диагностика уровня развития познавательного интереса В результате изучения психолого-педагогической литературы ...

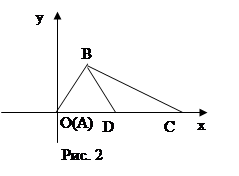





0 комментариев