Навигация
2. Произведение
Событие C называется произведением A и B, если оно состоит из всех событий, входящих и в A, и в B.
Пример: С=А∙В (А- выпадет 3, В – выпадет нечетное число). Тогда С состоит в выпадении только числа 3, так как 3 является нечетным числом.
3.Противоположное
Событие называется противоположным событию A, называется событие, состоящее в непоявлении события А. Обозначается противоположное событие символом ![]() .
.
Пример: Противоположными событиями являются промах и попадание при выстреле, или выпадении герба или цифры при одном подбрасывании монеты.
Вероятность событий
а)статистический подход.
Рассмотрим некоторое количество испытаний, в результате которых появилось событие А. Пусть было произведено n испытаний, в результате которых событие А появилось ровно m раз. Тогда отношение ![]() - называют относительной частотой.
- называют относительной частотой.
Также при большом количестве повторений испытания частость событий мало изменяется и стабилизируется около определенного значения, а при небольшом количестве повторений она может принимать различные значения. Каждое такое значение в конкретном случае принято называть вероятностью события А и обозначают Р(А).
Так как n всегда больше либо равно N, то вероятность заключена в интервале: ![]() .
.
Примером может служить выпадение герба или цифры при бросании монеты, которое является простым и наглядным испытанием. Практика человека говорит о том, что при большом числе бросаний примерно в 50% испытаний выпадет герб, а в 50% – цифра. А это уже определенная закономерность. Здесь нас интересует не результат отдельного подбрасывания, а то, что получится после многократных подбрасываний.
б)классическое определение.
В некоторых случая вероятности событий могут быть легко определены исходя из условий испытаний. Пусть испытание имеет n возможных исходов, то есть событий, которые могут появиться в результате данного испытания. При каждом повторении возможно появление только одного из данных исходов (то есть все n исходов несовместны). Кроме того, по условиям испытания нельзя сказать какие исходы появляются чаще других, то есть все исходы являются равновозможными. Допустим теперь что при n равновозможных исходах интерес представляет событие А, которое появляется только при m исходах и не появляется при остальных n-m исходах. И принято говорить, что в данном испытании имеется n случаев, из которых m благоприятствуют появлению события А. В таком случае вероятность можно вычислить, как отношение числа случаев благоприятствующих появлению события А (т.е. m), к общему числу всех исходов n: ![]() .
.
Пример 1. Из колоды с 36 перемешанными картами наудачу извлекается одна карта. Извлечение каждой карты из 36 является равновозможным событием. Поэтому вероятность извлечения "короля" составляет 4/36 = 1/9, карты выбранной масти – 9/36 = 1/4, карты выбранного цвета – 18/36 = 1/2.
Пример 2. Бросают две игральные кости. Требуется найти вероятность того, что сумма очков делится на 5. Возможные суммы очков, делящиеся на 5, равны 5 и 10. Событию "сумма очков равна 5" благоприятствуют события (1; 4), (2; 3), (3; 2), (4; 1), а событию "сумма очков равна 10" – события (4; 6), (5; 5), (6; 4). Таким образом, число благоприятствующих исходов равно 7, общее число равновозможных исходов – 6 " 6 = 36, поэтому вероятность события "сумма очков делится на 5" будет 7/36.
Пример 3. Вероятность извлечения белого шара (событие Б) из урны, содержащей три черных и четыре белых шара: p(Б) = 4/7.
Занятие 21. В 9 классе 10 учебных предметов. Сколькими способами можно поставить в среду первый и второй уроки?
2. Для составления двух команд из 40 человек надо выбрать капитанов команд. Каким числом способов это можно сделать?
3. На три призовых места претендуют Вася, Дима и Коля. Каким числом способов могут распределиться призовые места?
4. Сколько существует трехзначных чисел, оканчивающихся тройкой?
5. В партии 10 лотерейных билетов выигрышными являются 5. Приобретено 3 билета. В скольких случаях среди них есть хотя бы один выигрышный?
6. Четыре футболиста, четыре хоккеиста и два баскетболиста хотят сфотографироваться, стоя в один ряд, но так чтобы представители одного вида спорта стояли рядом. Каким числом способов они могут сделать это?
7. В некотором царстве не было двух жителей с одинаковым набором зубов. Каково максимальное количество жителей этого государства?
8. В урне лежат 10 жетонов с числами 1, 2, 3, 4, …, 10. Из нее вынимают три жетона. Во скольких случаях сумма написанных на них чисел равна 9? Не меньше 9.
Занятие 31. Сколькими способами можно разложить в два кармана пять купюр достоинством в 10, 50, 100, 500 и 1000 рублей?
2. Из десяти волейбольных мячей, обозначенных цифрами от 1 до 10, нужно выбрать пять мячей так, чтобы среди выбранных был элемент мяч с номером 5. Сколькими способами это можно сделать?
3. Сколько можно составить пятибуквенных слов из 7 гласных и 25 согласных букв, если гласные и согласные должны чередоваться?
4. Сколькими способами можно разбить 20 футболистов на две команды так, чтобы одна содержала 3 человека, а другая 15 ?
5. Во скольких девятизначных числах все цифры различны?
6. Сколько различных пятизначных чисел можно записать из цифр числа 273485961 так, чтобы четные и нечетные цифры в числе чередовались?
7. Двадцать различных книг отдано двум продавцам. Сколькими способами они могут распределить, если все книги могут быть отданы одному продавцу?
Занятие 41. Брошены две игральные кости. Найти вероятность того, что: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна 8, а разность четырем; в) сумма выпавших очков равна восьми, если известно, что их разность равна четырем; г) сумма выпавших очков равна пяти, а произведение – четырем?
2. В ящике имеется 10 одинаковых деталей, помеченные номерами 1, 2, …, 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь №1; б) детали №1 и №2.
3. Какова вероятность того, что из шести отмеченных чисел в карточке «Спортлото» (игра из 49) k чисел будут выигрышными.
4. Известно, что среди 40 участников имеются 10 мастеров спорта. Среди всех участников случайным образом выбрали первую пятерку, найдите вероятность, что в этой пятерке присутствуют ровно 2 мастера спорта.
5. На карточках написаны буквы: А, З, И, К, Л, Т, У, У, Ф, Ь. Вынимают наугад одну карточку за другой и раскладывают в том порядке в каком они были вынуты. Найти вероятность того, что на карточках будет написано слово ФИЗКУЛЬТУРА.
6. Во всероссийском дне бега каждому участнику присваивался определенный четырехзначный номер. И была проведена акция всем тем у кого на номере встречаются два раза цифра 7 получают в подарок кружку. Определите сколько кружек должен приготовить спорткомитет.
Занятие 5Приведем основные правила, позволяющие определить вероятность появления сложного события, состоящего из более простых событий, вероятность которых нам известна.
1.Вероятность достоверного события равна единице: P(E)=1.
Похожие работы
... ; технологическая функция имеет подфункции экономии учебного времени и учебного материала, устранения его дублирования и т.д. ГЛАВА 4. СОДЕРЖАНИЕ ИСНТРУМЕНТАЛЬНО-МЕТОДОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПЕДАГОГИЧЕСКОЙ ИНТЕГРАЦИИ 4.1. Типология интегративно-педагогического исследования В связи с поднимаемой в данном параграфе проблемой большой интерес вызывает монография В.М.Полонского "Оценки ...
... общего, начального и среднего профессионального образования, обеспечивающей наиболее полную реализацию интересов и образовательных потребностей учащихся. Таким образом, можно выделить несколько вариантов организации профильного обучения. 1) Модель внутришкольной профилизации В этой модели общеобразовательное учреждение может быть однопрофильным и многопрофильным. 2) Модель сетевой ...
... упражнения нормализуют деятельность желудочно-кишечного тракта: желудочное и кишечное сокоотделение, активность пищеварительных ферментов, моторную активность и т.д. Регулярные занятия физической культурой, сопровождаемые потоотделением, не только совершенствуют терморегуляцию, но и обеспечивают систематический вывод из организма образовавшихся в процессе жизнедеятельности шлаковых веществ. ...
... . В современном мире, чтобы быть профессионально компетентным, педагога должен постоянно учиться, заниматься самообразованием и самореализовываться в педагогической деятельности. Поэтому при формировании профессиональной компетентности будущего педагога, необходимо вести деятельность по двум направлениям: подготовке студентов как будущих педагогов и работа с преподавателями. Учитывая сложность и ...
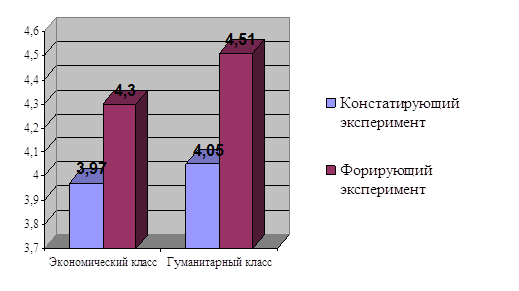
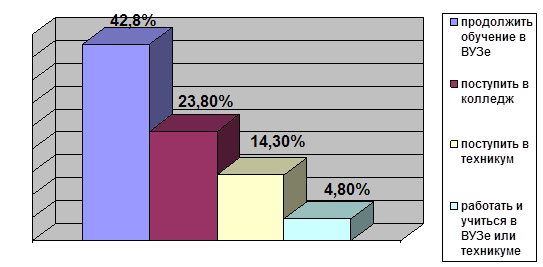
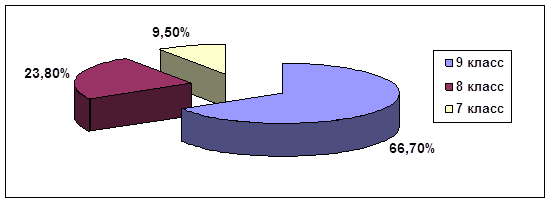
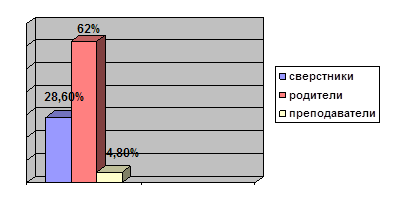
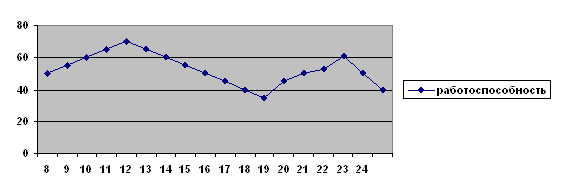
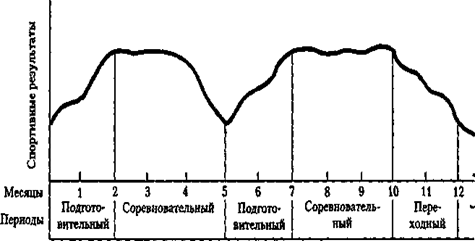
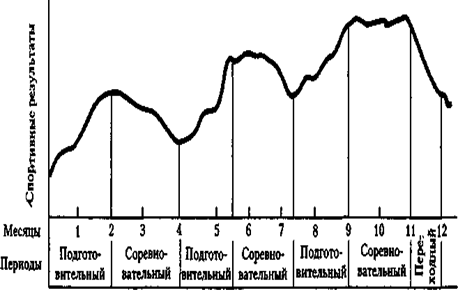

0 комментариев