Навигация
Множества и их численность. Ориентация в пространстве и во времени
1. Множества и их численность. Ориентация в пространстве и во времени.
/Образование множеств предметов, обладающих заданным свойствами. Практическое решение простых задач, иллюстрацией к которым служат конечные множества. Упорядочение предметов в множестве различными способами.
Название чисел от 1 до 20; счет предметов, сравнение предметов по определенным свойствам, сравнение множества предметов и установление отношений.
Знакомство с геометрическими фигурами: круг, треугольник, прямоугольник, квадрат, прямая и кривая линии.
Образование элементарных высказываний при характеристике свойств предметов и их взаимного расположения.
Определение численности множеств. Образование чисел путем прибавления и вычитания единицы. Цифры письменные и печатные. Числовые выражения для решения простых задач. Сравнение чисел. Состав чисел.
Сложение и вычитание чисел в пределах 20. Взаимосвязь сложения и вычитания. Название компонентов сложения. Знакомство с приемом подбора неизвестного компонента сложения и вычитания по заданной сумме или разности и другому компоненту.
Знакомство с целочисленным показанием времени по циферблату часов. Решение задач на определение начала и конца события, его продолжительность./
2. Величины.
/Измерение длин предметов непосредственным положением и «на глаз». Измерение длин отрезков. Сантиметр и сантиметровая линейка. Черчение отрезков заданной длины. Дециметр. Задачи на сравнение длин отрезков, на сложение и вычитание длин отрезков. знакомство с чашечными весами и взвешиванием. Килограмм./
3. Геометрические фигуры
/Знакомство с фигурами: точка, линия, прямая, кривая, ломаная, круг, треугольник, квадрат, прямоугольник, различные виды многоугольников./
4. Счет и арифметические действия над двузначными числами.
/Устная нумерация чисел в пределах 100. Состав числа 10. Разрядный состав чисел от 11 до 20. Приемы сложения и вычитания. Числовые выражения в 1 – 2 действия со скобками и без скобок; чтение, запись сравнение чисел от 11 до 20. Решение простых задач./
5. Повторение.
/Устная и письменная нумерация в пределах 20. Устная нумерация в пределах 100. Образование чисел, следующих за данным и предшествующих данному. Состав чисел. Образование простых и сложных высказываний при установлении закономерности используемых вычислительных приемов, при решении задач./
Основные требования к знаниям, навыкам и умениям учащихся подготовительного класса.
Учащиеся должны знать:
Последовательность чисел от 0 до 20; таблицу сложения чисел в пределах 10 и соответствующие случаи вычитания.
Учащиеся должны уметь:
Считать предметы в пределах 20; читать и записывать числа от 0 до 20; решать простые задачи на сложение и вычитание; сравнивать отрезки по длине; классифицировать предметы по одному свойству; строить отрицания простых высказываний.
На курс математики отводится – 112 ч.
Главная задача обучения математики в подготовительном классе – научить детей, опираясь на их опыт, ориентироваться в предметах так, чтобы самостоятельно находить ответы на вопросы, которые возникают, учить рассуждать, учить самостоятельно мыслить.
Проанализируем имеющиеся пособия по математике для подготовительных классов.
§ 2. Особенности учебных пособий по математике для
подготовительных классов.
Учебное пособие «Математика» для подготовительных классов авторов Н. И. Касабуцкого, А. Т. Катасоновой, А. А. Столяра, Т. М. Чеботаревской состоит из четырех частей. Для первого полугодия предназначены часть первая («Сравнение предметов и множеств предметов, пространственные и временные представления») и часть вторая («Однозначные числа»). Во втором полугодии используются часть третья («Двузначные числа») и часть четвертая («Величины»).
В учебное пособие включены три группы заданий: задания зоны актуального развития ребенка, дающие возможность проводить перспективно-опережающее обучение; задания зоны открытий, подготавливающие детей к установлению закономерности, к открытию правил, определенных свойств; задания зоны ближайшего развития, готовящие детей к самостоятельному поиску оригинальных решений в последующих темах в данном или следующих классах.
К перспективно - опережающим заданиям относятся:
1. Счет геометрических фигур из данного во вкладыше набора.
2. Практическое решение всех видов задач, для иллюстрации которых могут быть использованы геометрические фигуры набора.
Для достижения необходимого развивающего эффекта набор заданий должен быть подобран так, чтобы научить не только готовым знаниям, но и деятельности по их приобретению способом рассуждения, применяемом в математике.
Задания в учебном пособии «Математика» для подготовительного класса подобраны так, что учитель может создать на уроке ситуации, стимулирующие самостоятельное открытие учениками математических фактов, их доказательств, закономерностей, решений задач. Задания зоны актуального развития выполняются детьми самостоятельно; задания зоны открытий предусматривают проведение учителем беседы эвристического характера, в ходе которой дети индивидуальным путем приходят к открытиям; задания зоны ближайшего развития готовят детей к изучению дальнейших тем как в подготовительном классе, так и в последующих и выполняются под непосредственным руководством учителя.
Большое внимание уделяется первому разделу программы «Сравнение предметов и множеств предметов. Пространственные и временные представления» (часть 1 учебного пособия). Именно в дочисловой период начинается работа с простыми и сложными высказываниями при образовании множеств предметов, имеющих заданные свойства. («Положите на парту круги. Сколько среди них красных? Что вы можете сказать об одном из не красных кругов?»)
В практической деятельности с конкретными предметами дети впервые встречаются с решением задач. Заменяя яблоки кругами, а груши треугольниками, дети отвечают на вопросы учителя (решают простые задачи). Например:
«В вазе лежало 3 яблока и 4 груши. Сколько фруктов лежало в вазе» - простая задача, раскрывающая смысл сложения. Вопросы:
1) «Чего больше (меньше)? На сколько?»- простая задача на разностное сравнение.
2) «Из вазы взяли 2 яблока. Сколько яблок осталось в вазе?» - простая задача, раскрывающая смысл вычитания.
3) «Пять оставшихся фруктов разделили поровну между двумя детьми. По сколько яблок получил каждый? Что ты заметил?» - деление с остатком.
4) «Сколько фруктов нужно прибавить к 5, чтобы каждый ребенок получил по З? Почему?» - деление на равные части; задача, раскрывающая смысл умножения (при ответе на вопрос «Почему?»).»
В дочисловой период дети проводят счет предметов в пределах 20. Для этого они пользуются набором слов-числительных, знакомых им до школы. В некоторых случаях учитель помогает проговаривать эти слова. Устанавливая, сколько предметов в наборе, предложенном им, дети приходят к выводу, что, перебирая предметы по одному и не пропуская ни одного предмета, по последнему слову-числительному можно ответить на поставленный вопрос. В этот период с помощью предметов устанавливают и состав чисел от 2 до 10.
С помощью взаимно однозначного соответствия ученики устанавливают, в каком множестве предметов больше (меньше) и на сколько. Практически проводят уравнивание групп предметов двумя способами: прибавляют несколько предметов или убирают лишние.
Геометрические фигуры дети различают по форме (круглые, треугольные, квадратные, прямоугольные), по размерам (большие и маленькие) и по цвету (красные, желтые, зеленые). Набором геометрических фигур из вкладыша к части 1 учебного пособия учитель пользуется при неявном введении общелогических приемов: классификации (по одному, двум и трем свойствам), конкретизации, сравнения и сопоставления.
С помощью общелогических приемов индукции, дедукции, анализа и синтеза в учебное пособие отобраны задания, которые готовят учеников к открытию новых математических фактов во всех последующих темах программы.
Основной метод работы в дочисловой период - игра. Обучая детей-шестилеток в процессе игры, учитель должен стремиться к тому, чтобы радость от игровой деятельности постепенно перешла в радость обучения. Интерес - лучший стимул обучения.
Особое внимание необходимо обратить на интеллектуальные игры, в которых в доступной форме вводятся общелогические приемы рассуждений. Это игры: «Кто где живет?», «Заполни квадраты», «Вычислительная машина», «Чудо-мешочек», «Преобразуй слово», «Игра с одним обручем», «Игра с двумя обручами», «Игра с тремя обручами».
Тема «Однозначные числа» вводится в части 2 учебного пособия. Назовем основные направления работы по этой теме:
1) Отвлечение чисел от конкретных равночисленных множеств предметов различной природы, их рукописное и печатное обозначение.
2) Расположение чисел на луче: 1; 2; 3; 4; 5; 6; 7; 8; 9
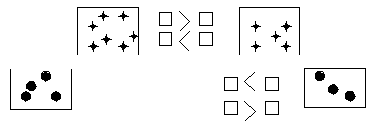
3) Сравнение чисел, использование знаков <, >, = для составления истинных высказываний.
4) Получение числа, следующего за данным, прибавлением 1 и числа, предшествующего данному, вычитанием 1. Введение базовых приемов сложения и вычитания 1 осуществляется через задачи и на числовом луче.
5) Раскрытие состава чисел проводится также с опорой на наглядность. Используется состав чисел для введения новых вычислительных приемов сложения и вычитания по частям, перестановкой слагаемых:
5+4=5+1+1+1+1=5+1+3=5+2+2=5+3+1, 9-4=9-1-1-1-1=9-1-3=9-2-2=9-3-1, 2+5=5+2=5+1+1.
6) Установление взаимосвязи между сложением и вычитанием. К любому примеру на сложение следует составить два примера на вычитание, а к любому примеру на вычитание пример на сложение и вычитание.
3+2=5 7-2=5 5-2=3 7-5=2 5-3=2 5+2=7
Действие вычитание следует использовать и при сравнении чисел (как подготовка к решению задач на разностное сравнение) 2<7 7-2=5;9>5 9-5=4.
7) Подготовка детей к теме "Двузначные числа". Для этого можно пользоваться набором слов-числительных и предлагать задания перспективно - опережающего характера: 5+2=7. Пятнадцать и два - это сколько? Или 5 - 3 = 2, а пятнадцать без трех - это сколько?
В теме «Двузначные числа в пределах 20» (часть 3) проводится отработка введенных в части 2 вычислительных приемов сложения и вычитания. Таблица сложения и вычитания в пределах 10, в соответствии с требованиями программы, обязательна для запоминания, а знание таблицы сложения и вычитания однозначных чисел с переходом через десяток в пределах 20 обязательным не является. Важно, чтобы дети и по этой таблице закрепили вычислительные приемы и заметили закономерность: 1) прибавляем (вычитаем) до 10; 2) прибавляем (вычитаем) остальное.
В этой теме вводится понятие «разряд», и двузначные числа от 10 до 20 записываются в таблице разрядов.
Числа могут быть результатом не только счета предметов, но и измерения длин, объемов, масс. Выделение темы «Величины и их измерение» (часть 4) подчеркивает важность представлений о величинах и процесс их измерения. Последняя, четвертая тема программы прежде всего систематизирует то, что уже известно детям из их собственного опыта, из предыдущих тем. Она несколько расширяет и уточняет эти сведения.
В частях 2-4 особое место занимают примеры с «окошками». Их назначение - научить детей рассуждать. Например: 5+□=9. Поставим в пустую клеточку число 1. Получаем, что 5+1=9. Это неверно. Проверим число 2: 5 + 2 = 9 - неправильно. Число 3 дает 5+3=9. Это тоже неправильно. А вот число 4 подходит, так как 5 + 4 = 9. Для того чтобы сократить поиск, предлагаем детям понаблюдать за тройками чисел в примерах на сложение и вычитание. Учащиеся устанавливают закономерности:
1) самое большое число при сложении - сумма; 2) слагаемые (если одно из них не равно нулю) меньше суммы; 3) самое большое число при вычитании - уменьшаемое; разность и вычитаемое (если одно из них не равно нулю) меньше уменьшаемого; 4) слагаемое - не самое большое число, поэтому его находят действием вычитания над числами, данными в примере; 5) уменьшаемое - самое большое число в примере, поэтому его находят действием сложения над числами примера; 6) вычитаемое - не самое большое число в примере на вычитание, поэтому его находят действием вычитания.
Эти наблюдения в дальнейшем перейдут в правила проверки и в правила нахождения неизвестных компонентов действий сложения и вычитания.
В школах ряда регионов Республики Беларусь прошли массовую апробацию учебно-методические пособия для I – IV классов учебное пособие по математике Герасимова В. Д. Рассмотрим, как учитываются особенности обучения математики детей шестилетнего возраста в данном пособии.
Содержание пособия во многом служит обеспечению ведущей роли теоретических знаний, обучению на высоком уровне сложности, достаточно быстрому темпу изучения программного материала.
Основные этапы построения содержания учебника математики:
1. Системный подход к построению содержания математического образования.
2. Психологические аспекты усвоения курса школьной математики.
3. Текстовые задачи:
А) анализ текста задачи.
Б) поиск и составление плана решения.
В) оформление решения. Проверка.
Решение задач от простых к сложным.
4. Числа и действия с ними. Уравнения.
5. Элементы геометрии.
Данный учебник активизирует познавательную способность учащихся, развивает их познавательные способности и самостоятельность.
В учебнике много развивающих игр. Каждый урок начинается с игры. Это и игры «Сколько?», «Фотограф», «Найди целое и части», «Восстанови число». С каждым уроком игры усложняются.
Грамотное построение материала учебника позволяет на уроке использовать карточки для устного счета, математические диктанты, тексты для самостоятельных и контрольных работ. Учебник является одновременно и рабочей тетрадью, для совместного творчества родителя и ребенка, учителя и ученика. Учебник построен так, чтобы ребенок мог самостоятельно шаг за шагом освоить школьную программу по математике. Новые понятия не даются детям в готовом виде, а «открываются» ими в процессе работы. Все задания учебника учат ребенка рассуждать, доказывать свою точку зрения, делать выводы, четкость и ясность изложения, наглядные примеры и образцы рассуждений позволяют понять и усвоить тем даже тем детям, у которых «душа не лежит к математике».
Основные темы, с которых начинается изучение математической науки – это натуральный ряд чисел, арабская и римская нумерация, целое и часть, как основа к решению уравнений, задач, развитие устных и письменных вычислений. С самого начала в учебном пособии идет упор на наглядно-образное мышление детей, используется игра «Сколько?» (карточка с изображением кружков от 1 до 10). Легко вводится понятие натурального ряда чисел, учащиеся запоминают образ цифры и соответствующий рисунок. Позже вводится двухцветный вариант игры. Это легко позволяет ребенку усвоить понятие части и целого, что в дальнейшем помогает также спокойно перейти к решению задач. Используя эту игру можно достичь высоких результатов и при формировании вычислительных навыков. Ученики, глядя на карточку составляют ряд простых высказываний на сложение и вычитание. Для числа «9» : 7 + 2 = 9; 2 + 7 = 9; 9 – 2 = 7; 9 – 7 = 2. Ученики представляют данное число в виде частей 2 и 7 и целого – 9. Такие упражнения легко помогают перейти к решению примеров, выполнению проверок, решению примеров с «окошками», которые потом заменяют буквами и к решению задач. В целях усвоения структуры текстовой задачи автором творчески применяется прием перехода от рассказа к задаче.
Работа с алгоритмом позволяет ученику четко определить границы заданного.
Большое количество заданий для каждого уровня позволяет учителю делать выбор, дифференцированно подходить к возможности ученика, к уровню развития каждого.
§ 3. Приемы организации умственных действий на уроках
математики с детьми шестилетнего возраста.
Развитие учащихся во многом зависит от той деятельности, которую они выполняют в процессе обучения. Эта деятельность может быть репродуктивной и продуктивной. Они тесно связаны между собой, но в зависимости от того, какой вид деятельности преобладает, обучение оказывает различное влияние на развитие детей.
Репродуктивная деятельность характеризуется тем, что ученик получает готовую информацию, воспринимает ее, понимает, запоминает, затем воспроизводит. Основная цель такой деятельности – формирование у школьников знаний, умений, навыков, развитие внимания и памяти.
Продуктивная деятельность связана с активной работой мышления и находит свое выражение в таких мыслительных операциях, как анализ и синтез, классификация, аналогия, обобщение. Эти мыслительные операции в психолого-педагогической литературе принято называть логическими приемами мышления или приемами умственных действий.
Включение этих операций в процесс усвоения математического содержания – одно из важных условий построения развивающего обучения. Овладение ими не только обеспечивает новый уровень усвоения, но дает существенные сдвиги в умственном развитии ребенка.
Рассмотрим возможности активного включения в процесс обучения математики различных приемов умственной деятельности приемлемых для детей шестилетнего возраста.
Важнейшими мыслительными операциями являются анализ и синтез
Анализ связан с выявлением элементов данного объекта, его признаков или свойств. Синтез – это соединение различных элементов, сторон объекта в единое целое. В мыслительной деятельности человека анализ и синтез дополняют друг друга, так как анализ осуществляется через синтез, синтез – через анализ. Способность к аналитико-синтетической деятельности находит свое выражение не только в умении выделять элементы того или иного объекта, но и в умении включать их в новые связи, увидеть их новые функции.
Формированию этих умений может способствовать: а) рассмотрение данного объекта с точки зрения разных понятий; б) постановка различных заданий к данному математическому объекту.
Для рассмотрения данного объекта с точки зрения различных понятий или с различных точек зрения, младшим школьникам при обучении математике можно предложить такие задания:
- Как по-разному можно назвать квадрат? (прямоугольник, четырехугольник, многоугольник, ромб)
- По каким признакам можно разложить предметы в коробки? (даны предметы: пуговицы разных размеров, форм, цвета)
- Разгадай правило, по которому составлена таблица и заполни пропущенные клетки:
| 4 | 6 | 9 | 3 | 8 | 6 | 5 | 2 | ||
| 5 | 7 | 8 | 2 | 4 | 6 |
Увидев, что в данной таблице две строки, учащиеся пытаются выявить определенное правило в каждой из них, выясняют, на сколько одно число больше (меньше) другого. Для этого они выполняют сложение и вычитание. Не обнаружив закономерность в верхней строке, они пытаются анализировать данную таблицу с другой точки зрения, сравнивая каждое число верхней строки с соответствующим (стоящим под ним) числом нижней строки. Получаем: 4<5 на 1; 6<7 на 1; 9>8 на 1; 3>2 на 1. Если под числом 8 записать число 9, а под числом 6 – число 7, то имеем: 8<9 на 1; 6<7 на 1, значит 5>□ на 1; □>4 на 1.
Прием сравнения играет особую роль в организации продуктивной деятельности шестилеток в процессе обучения математики. Формирование умения пользоваться этим приемом надо осуществлять поэтапно, ориентируясь на такие этапы:
1. выявление признаков или свойств одного объекта;
2. установление сходства различия между признаками двух объектов;
3. выявление сходства между признаками трех, четырех и более объектов.
В качестве объектов можно использовать предметы или рисунки с изображением предметов, хорошо знакомых детям, в которых они могут выделить те или иные признаки, опираясь на имеющиеся у них представления.
Для организации деятельности учащихся, направленных на выявление того или иного признаков, можно сначала предложить такой вопрос:
- Что вы можете рассказать о предмете? (яблоко большое, красное; тыква желтая, большая, с полосками, хвостиком; круг – большой, зеленый; квадрат – маленький, желтый).
В процессе работы учитель знакомит детей с понятиями «размер», «форма» и предлагает им следующие вопросы:
- Что вы можете сказать о размерах (формах) этого предмета?
- В чем сходство и различие этих предметов? – что изменилось?
Возможно познакомить их с термином «признак» и использовать его при выполнении заданий: «Назови признаки предмета», «Назови сходные и различные признаки предметов».
Умение выделять признаки и, ориентируясь на них, сравнивать предметы ученики переносят на математические объекты.
Для организации самостоятельной познавательной деятельности учащихся в подготовительном классе нужно использовать метод наблюдений. В процессе наблюдений ученики анализируют, сравнивают, делают вывод. Полученные таким образом знания являются более осознанными и лучше усваиваются.
Для того, чтобы дети умели последовательно излагать свои мысли, переходя от одного суждения к другому, с первых шагов обучения следует учить их рассуждать. Необходимо, чтобы результаты своих наблюдений дети фиксировали с помощью математической записи. Например: на одной чашке весов гиря в 3 кг, а на другой в 2 кг. Затем на каждую чашку весов добавляются гири по 5 кг. Ход рассуждений фиксируется в записи: 3>2, 3+5>2+5, 5=5. Данное задание позволяет организовать наблюдения учащихся, в процессе которого они самостоятельно приходят к выводам.
Ученик должен осознать практическую значимость сравнения, т. е. сравнение должно быть решением той или иной задачи. С целью проведения работы в данном направлении учитель может использовать следующие задания:
1. 6 + 1 = 7. Сколько надо прибавить к 6, чтобы получить не 7, а 8?
2. 5 + 2 = 7, 2 + … = 7. Какое число надо поставить вместо точек, чтобы второе равенство было верным? Почему?
3. 5 + 3, 5 + 4. Могут ли в данных примерах получиться одинаковые ответы?
Умение выделить признаки предметов и установить между ними сходство и различие – основа приема классификации.
Из курса математики известно, что при разбиении множества на классы необходимо выполнять следующие условия: 1) ни одно из подмножеств не пусто; 2) подмножества попарно не пересекаются; 3) объединение всех подмножеств составляет данное множество. Предлагая детям задания на классификацию, эти условия необходимо учитывать. Сначала выполняются задания на классификацию хорошо известных предметов и геометрических фигур. Например: учащиеся рассматривают предметы: огурец, помидор, молоток, капуста, лук, свекла, редька. Ориентируясь на понятие «овощ», они могут разбить множество предметов на два класса: овощи – не овощи.
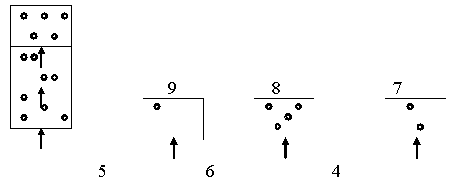
Для упражнений в счете детям можно предложить иллюстрации, к которым можно поставить вопросы, начинающиеся со слова «Сколько …?». («сколько больших кругов?», «сколько красных больших кругов» и т. д.)Упражняясь в счете учащиеся овладевают логическим приемом классификации.
Задания, связанные с приемом классификации, обычно формулируются в таком виде: «Разбей (разложи) все предметы на две группы по какому-то признаку». Большинство детей успешно справляются с этим заданием, ориентируясь на такие признаки, как цвет и размер. По мере изучения различных понятий задания на классификацию могут включать числа, выражения, равенства, геометрические фигуры.
При изучении сложения и вычитания в пределах 10 возможны такие задания на классификацию:
Разбей данные выражения на группы по какому-то признаку:
А) 3+1, 4-1, 5+1, 6-1, 7+1, 8-1. (в этом случае основания для разбиения на две группы дети легко находят, так как признак представлен явно в записи выражения).
Но можно представить и другие выражения:
Б) 3+2, 6-1, 4+5, 9-2, 4+1, 7-2, 10-1, 6+1, 3+4. (разбивая на группы данное множество выражений, ученики могут ориентироваться не только на знак арифметического действия, но и на результат.) В данном случае необходимо указать количество групп разбиения.
Задания на классификацию можно давать не только для продуктивного закрепления знаний, умений и навыков, но и при знакомстве учащихся с новыми понятиями. Например, для определения понятия «прямоугольник» к множеству разнообразных четырехугольников и других геометрических фигур можно предложить такие задания и вопросы:
Убери «лишнюю» фигуру; чем похожи все остальные, чем они различаются? Как можно назвать фигуры? Покажите четырехугольники с одним прямым углом, с двумя, с тремя, с четырьмя. Разбей четырехугольники на группы по количеству прямых углов.
Таким образом, при обучении математики можно использовать задания на классификацию различных видов:
1. Подготовительные задания. К ним относятся: «Убери (назови) лишний предмет», «нарисуй предмет такого же цвета (формы, размеров)», «Дай название группе предметов». Сюда же можно отнести задания на развитие внимания и наблюдательности: «Какой предмет убрали?», «Что изменилось?»
Похожие работы
... познание неразрывно связано с воображением и действованием, совершаемым свободно, по внутреннему побуждению. В нашем исследовании рассмотрено подробно интеллектуальная одаренность детей и ее соотношение с творческой одаренностью. Соотношение творческой и интеллектуальной одаренности рассматривали многие психологи. Сторонники сведения творческих способностей к интеллекту опираются на результаты ...
... интересует. Соблюдение принципа наглядности – одно из основных требований, которому должно удовлетворять обучение математике в начальных классах. В начальных классах эффективно использовать технические средства обучения (ТСО) и наглядность по несколько минут на различных этапах урока. В процессе работы важно применять технические средства обучения в комплексе с другими средствами наглядности, ...
... нецелесообразности перенесения содержания и методов школьного обучения на эту ступень. Отметим, что совершенствование преемственности в работе детского сада и школы обеспечит условия успешного обучения в первом классе. При этом важно знание воспитателями основных подходов в методике обучения математике в первом классе, ознакомление их с современными учебниками. Сформировать готовность к обучению ...
... росту. Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике. Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр 2.1 Дидактические игры, их виды В отличие от других видов деятельности игра содержит цель в самой себе; ...
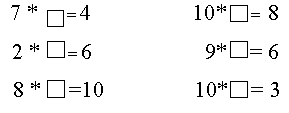
0 комментариев