Навигация
Задания, в которых на основе классификации указывает учитель
2. Задания, в которых на основе классификации указывает учитель.
3. Задания, при выполнении которых дети сами выделяют основание классификации.
В процессе обучения математики учитель довольно часто говорит детям: «Сделайте по аналогии» или «Это аналогичное задание». Аналогия – это сходство в каком-либо отношении между предметами, явлениями, понятиями, способами действий.
Формируя у шестилетних детей выполнять умозаключения по аналогии, необходимо иметь в виду следующее: аналогия основывается на сравнении, поэтому успех ее зависит от того, на сколько ученики умеют выделять признаки объектов, устанавливать сходства и различия между ними. Для использования аналогии необходимо иметь два объекта, один из которых известен, второй сравнивается с ним по каким-либо признакам, необходимо сравнивать признаки объектов; существенные в данной ситуации.
Непременным условием развивающего обучения является формирование у учащихся способности обосновать те суждения, которые они высказывают, т. е. умение рассуждать. Для сознательного выполнения дедуктивных умозаключений необходима большая подготовительная работа, направленная на усвоение вывода, закономерности, свойства в общем виде, связанная с развитием математической речи учащихся. Например, довольно длительная работа по усвоению принципа построения натурального ряда чисел позволяет учащимся овладеть правилом прибавления к любому числу 1. Составляя таблицы □+1 и □-1, ученик пользуется этим правилом как фактической посылкой, выполняя тем самым дедуктивные рассуждения. Эта посылка используется и при сравнении чисел 4 и 5.
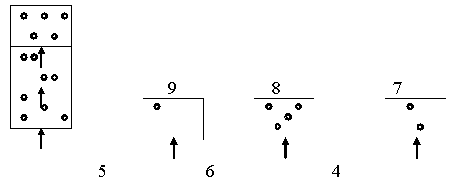
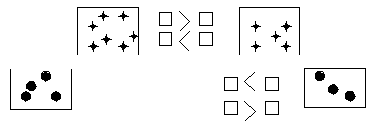
При сравнении выражений (6+2 и 6+3; 6+4 и 4+6) ученики часто пользуются сравнением после вычисления выражений. Если детям предложить сравнить числа не прибегая к вычислениям, то они делают элементарные умозаключения, обоснованные на знании правила увеличении числа на 1.
Умение последовательно и непротиворечиво излагать свои мысли тесно связано с умением представлять сложные действия в виде организованной последовательности простых, т. е. построения алгоритма. Начинать работу по составлению алгоритмов необходимо с доступных и понятных детям действий. Например: переход улицы с нерегулируемым и регулируемым перекрестком, приготовление какого-либо блюда. При этом сам термин «алгоритм» можно не вводить. Для подготовительного класса можно использовать алгоритм при сравнении чисел и величин, при решении задач, при изучении темы «состав числа», при решении примеров «с окошками». В подготовительный период полезно играть в игру «робот». Суть игры в том, что имеется робот, который понимает четыре команды: «Вперед», «Назад», «Вправо», «Влево». Нужно научиться управлять им. В качестве робота могут выступать сами дети. Они будут выполнять команды, которые им предлагают другие школьники.
Можно предложить следующие упражнения, связанные с алгоритмом в подготовительном классе: 1) исполнение и составление алгоритма из окружающей жизни; 2) изменение алгоритма; 3) построение алгоритмов, приводящих к одному результату; 4) исполнение и построение алгоритма на геометрическом материале; 5) построение простейших циклических алгоритмов. В учебных пособиях по математике для подготовительного класса подобрано на алгоритмизацию достаточное количество заданий.
§ 4. Обучение решению задач шестилеток.
Работа с задачами является важным аспектом обучения математики. Для эффективной работы необходимо, чтобы каждая задача давала пищу для интенсивной умственной деятельности учащихся, а ученик приступал к ее решению, рассчитывая на успех.
Вводить задачи в подготовительном классе целесообразно с некоторой задержкой, не раньше второй четверти.
На начальном этапе обучению решению задач строится рассказ по картинкам учебного пособия. Эти рассказы позволяют сформировать у детей умение выделять свойства предметов, отличать их существенные и несущественные свойства, способствуют формированию понятия об общих и отличительных свойствах, овладению математическим языком. Далее следует предлагать задания по выделению фигур из сложного чертежа. Задания дают возможность продвигать детей в умении анализировать и синтезировать объекты, сравнивать производимые действия и их результаты, способствуют расширению математического кругозора, формированию связной, грамотной речи.
Задания по преобразованию фигур. Чаще такие задания называют «геометрия на спичках». Задания этого вида можно разделить на две группы: а) преобразование фигур, достигаемое изменением числа палочек; б) преобразование фигур без изменения числа палочек. Однако решению основных групп заданий необходимо предпослать работу над заданиями, которые можно назвать вспомогательными, в ходе которых дети знакомятся с основными подходами к решению основных заданий.
Рассмотрим рассказ по рисунку. Здесь можно составить следующие рассказы:
1. На ветке висит 4 груши, а на земле лежат еще 2 груши. Всего нарисовано 6 груш.
Этот рассказ наиболее естественно передает то, что изображено на рисунке.
2. На ветке росло 6 груш. Подул ветер и две груши упали на землю, а 4 груши остались на ветке.
Второй рассказ в отличие от первого требует мыслительного обращения к ситуации. В основе второго рассказа лежит математическая операция – разбиение множества на два подмножества.
По мере продвижения от задания к заданию все большее место должна занимать самостоятельная деятельность учащихся.
Другой характер носит работа по двум связанным между собой рисункам. Разбор и истолкование рисунков позволяет сохраняя разносторонний подход к рассмотрению объектов, изображенных на рисунке, подвести учащихся к созданию текстов, которые являются задачами.
Во II и III четверти начинается работа, включающая анализ текста задачи и ее решения. Умение решать задачу закономерно вытекает из умения работать с текстом. Можно выделить четыре этапа решения задачи: понимание постановки задачи; составление плана решения; осуществление плана решения; анализ полученного решения. После того, как дети будут правильно делить задачу на части, вводят термин «условие задачи» и «вопрос задачи». Затем вводят понятия «данные» и «искомое».
Самое главное при решении задач не количество решенных однотипных задач, а осмысление содержание задачи, правильного логического рассуждения. Решение двух аналогичных задач следует разделять во времени.
При решении составленных задач в подготовительном классе необходима постановка вопросов в письменном или устном виде. Это позволяет более отчетливо осмыслить ход решения. Также необходимо, чтобы дети по-разному умели записывать решение задачи, чтобы они могли реализовать тот или иной вид записи соответственно требованию, которое предъявляется им в данный момент.
Для лучшего осмысления математических связей, заложенных в задаче, большое значение имеет краткая запись условия задачи.
Не все учащиеся могут дать правильный ответ при решении задачи. Необходимо, чтобы дети размышляя, используя схему, рисунок приходили к правильному решению.
Развивать надо все: память, внимание, мышление, математическую речь, умение сопоставлять, сравнивать, обобщать и доказывать. В этом огромную помощь оказывают логические задачи. Они вырабатывают привычку детей разносторонне мыслить, проводить более глубокий анализ задач, развивать речь учащихся.
§ 5. Урок математики в подготовительном классе.
Структура урока математики в подготовительном классе соответствует особенностям мышления и памяти шестилетних детей:
I. Коллективная работа учителя с классом, когда в ходе игровой деятельности выполняются задания зоны актуального развития, готовящие детей к открытию нового материала (до 10 мин.)
II. Физкультпауза (до 2 мин.).
III. Работа с теми заданиями, которые дают возможность учителю системой вопросов и практических заданий подвести детей к открытию материала, соответствующего теме урока (до 10 мин.)
IV. Физкультпауза (до 3 мин.).
V. Работа по выполнению задания зоны ближайшего развития. Письмо на разлиновке в клетку. (до 10 мин.)
VI. Итог урока.
При построении конкретного урока необходимо учитывать не только определенные этапы обучения, такие как актуализацию знаний, объяснение нового, закрепление, контроль, повторение; не только специфику математического содержания, но и основную цель курса, его логику, и те методические подходы, которые способствуют ее достижению и находят отражение в учебных пособиях по математике. Так как в рамках обучения, нацеленного на отработку знаний, умений, навыков, новый материал небольшими частями рассматривается почти на каждом уроке, то наиболее распространенным типом урока математики в подготовительном классе является комбинированный урок. Внешняя структура уроков комбинированного типа может быть различной: 1) закрепление и проверка знаний ранее изученного материала; 2) изучение нового материала; 3) закрепление этого материала; 4) итоги урока; или 1) изучение нового материала; 2) закрепление изучаемого на данном уроке и ранее пройденного материала; 3) подготовительная работа к изучению новой темы; 4) итоги урока.
Внутренняя сторона уроков находит отражение в учебных пособиях по математике для подготовительных классов.
В подготовительном классе специальных уроков математики, целиком посвященных изучению нового материала нет. Как говорилось выше, новый материал небольшими частями рассматривается на каждом уроке. Но бывают уроки, на которых изучение нового материала является основной дидактической целью. Этой работе отводится большая часть урока, при этом другие части урока также подчинены изучению нового материала. Помимо знакомства с новым материалом на таком уроке происходит первичное закрепление полученных знаний. Структура такого урока может быть следующей: 1) повторение материала, необходимого для сознательного усвоения новых математических знаний; 2) изучение нового материала; 3) первичное закрепление изучаемого материала; 4) итоги урока. На уроках закрепления знаний, умений и навыков основное место занимает выполнение учащимися различных тренировочных упражнений и творческих работ. Большое место в этих уроках отводится самостоятельной работе учащихся. Структура этих уроков следующая: 1) воспроизведение учащимися знаний, умений и навыков, которые потребуются для выполнения заданий; 2) самостоятельное выполнение учащимися различных упражнений; 3) проверка выполнения работы и подведение итогов урока. Основное место на уроках контроля знаний и умений отводится проверочной работе, которая проходит или в устной, или в письменной форме. Проверка, как правило сочетается с закреплением знаний, умений и навыков. Проверочные письменные или устные работы занимают не более 20 – 25 минут, остальное время отводится на закрепление ранее изученного.
В конце любого урока должна быть дана обязательная оценка работы всех детей. В подготовительном классе должна даваться только положительная оценка работы каждого ученика в словесной форме, никаких других оценок быть не должно.
Глава 3. Дидактические игры в процессе обучения детей на уроках
математики.
§ 1. Роль игры.
Возраст ребенка с шести до семи лет принято считать переходным. С одной стороны, этот возраст можно назвать старшим дошкольным, если ребенок обучается в детском саду. С другой стороны – младшим школьным, потому что с приходом в школу ребенок погружается в учебную деятельность. Однако ведущей деятельностью для детей данного возраста, независимо от того, где проходит его обучение, является игра, в которой формируются предпосылки потребности в учебной деятельности в виде познавательных интересов. В процессе развития сюжетной игры у детей развивается воображение и символическая функция; дети получают разнообразные сведения об окружающем мире, о взрослых людях, умении ориентироваться в этих сведениях, согласно их содержанию. Преимущественно познавательную нагрузку, функцию интеллектуального развития берут на себя дидактические игры, используемые педагогом в учебно-воспитательных целях как средство стимулирования активности психических процессов. Решающее значение для формирования непосредственных предпосылок для учебной деятельности имеют игры по правилам. В них ребенок учится сознательно подчиняться правилам, начинает обращать внимание на способ достижения результата, а не только на собственный результат.
С приходом в школу игра продолжает оставаться базисом для удовлетворения познавательных интересов и воображения ребенка, выступает психологической предпосылкой потребности в усвоении уже теоретических знаний. Учебная деятельность имеет специфическую структуру, включающую в себя: 1) учебные задачи; 2) учебные действия; 3) контроль;4) оценку. Но усвоение теоретических знаний возможно при сформированности у детей шестилетнего возраста познавательной мотивации и определенных навыков и умений в учебной деятельности. К основным навыкам учебной деятельности относятся: 1) восприятие и осознание учебной задачи; 2) выполнение ориентировочных и исполнительских действий; 3) контроль за правильностью и качеством учебных действий; 4) оценка собственной работы.
К основным умениям учебной деятельности относятся: 1) умение с помощью педагога и самостоятельно ставить познавательные задачи; 2) умение анализировать задачи, находить общий способ действий; 3) планировать самостоятельную деятельность; 4) подбирать способы решения задач и контролировать правильность их выполнения, производя самокоррекцию своих ошибок и ошибок сверстников; 5) умение оценивать собственные действия и результат, фиксировать соответствие или несоответствие результатов согласно требованию учебной ситуации.
§ 2. Игры на уроках по темам: «Сложение и вычитание»,
«Величины и их измерения».
Рассмотрим на примере уроков по темам: «Сложение и вычитание», «Величины и их измерение» роль дидактических игр.
Урок по учебному пособию В. Д. Герасимова.
Тема урока: «Сложение и вычитание. Знаки «+» и «-»».
Цель урока: 1. Совершенствовать навык сложения и вычитания, устных вычислений в пределах 10; прямого и обратного счета. Учить различать геометрические фигуры.
2. Развивать сообразительность, моторику руки, логическое мышление учащихся.
3. Воспитывать навыки правильного поведения на уроке, усидчивость, интерес к изучению математики.
Оборудование: планшет с геометрическими фигурами, собранными в форме корабля.
|
1. Организация класса.
2. Устный счет.
3. Работа с учебным пособием.
4. Физкультминутка.
Ход урока:
1. Организационный момент. Постановка цели.
Организация класса.
Ребята, а вы любите путешествовать? Сегодня мы отправимся с вами в путешествие по морю. Этот путь будет интересным, увлекательным и трудным. А преодолеть трудности нам помогут знания по математике. Мы будем считать предметы, заниматься сложением и вычитанием, решать задачи.
Похожие работы
... познание неразрывно связано с воображением и действованием, совершаемым свободно, по внутреннему побуждению. В нашем исследовании рассмотрено подробно интеллектуальная одаренность детей и ее соотношение с творческой одаренностью. Соотношение творческой и интеллектуальной одаренности рассматривали многие психологи. Сторонники сведения творческих способностей к интеллекту опираются на результаты ...
... интересует. Соблюдение принципа наглядности – одно из основных требований, которому должно удовлетворять обучение математике в начальных классах. В начальных классах эффективно использовать технические средства обучения (ТСО) и наглядность по несколько минут на различных этапах урока. В процессе работы важно применять технические средства обучения в комплексе с другими средствами наглядности, ...
... нецелесообразности перенесения содержания и методов школьного обучения на эту ступень. Отметим, что совершенствование преемственности в работе детского сада и школы обеспечит условия успешного обучения в первом классе. При этом важно знание воспитателями основных подходов в методике обучения математике в первом классе, ознакомление их с современными учебниками. Сформировать готовность к обучению ...
... росту. Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике. Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр 2.1 Дидактические игры, их виды В отличие от других видов деятельности игра содержит цель в самой себе; ...
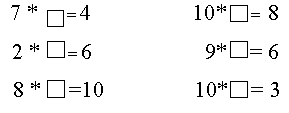
0 комментариев