Навигация
Умножение матриц. Свойства
1.3.3 Умножение матриц. Свойства
![]() Как сложить две матрицы?
Как сложить две матрицы?
Опр. Суммой матриц ![]() и
и ![]() размерности
размерности ![]() называется матрица
называется матрица ![]() размерности
размерности ![]() .
.
Пример.
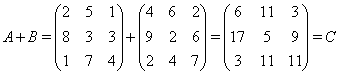
Как суммировать матрицы вы уже знаете. Теперь придумайте как умножить матрицу на число.
Опр. Произведением ![]() матрицы
матрицы ![]() размерности
размерности ![]() и числа
и числа ![]() называется матрица
называется матрица ![]() размерности
размерности ![]() .
.
Пример.
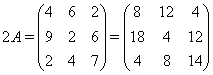
Кроме введенных операций нам понадобится умножение матриц.
Опр. Произведением матриц ![]() и
и ![]() называется матрица
называется матрица ![]() , где
, где ![]()
Необходимо показать и озвучить практический способ умножения матриц: строка умножается на столбец. Берем первую строку матрицы А, ставим ее вертикально напротив первого столбца матрицы В, умножаем элементы этой строки и столбца, которые стоят напротив др.др., складываем произведения. Это первый элемент матрицы С. Теперь таким же образом умножаем эту строку на второй столбец - получаем второй элемент первой строки матрицы С. И т.д. Получим первую строку новой матрицы. Для того, чтобы получить вторую строку, проделываем тоже самое со второй строкой матрицы А.
Пример.
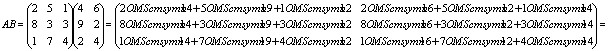
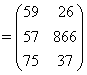
Задача 1. Выполнить умножение.
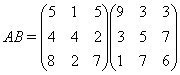
![]()
1.3.4 Домашнее задание
Задача 2. Выполнить умножение.
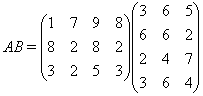
1.4 Четвертый урок
![]()
1.4.1 Проверка домашнего задания
1.4.2 Транспонирование
Опр. Замена строк матрицы на ее столбцы (а стольбцов на строки) называется транспонированием. Обозначается ![]() .
.
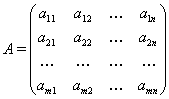
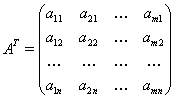
Пример.
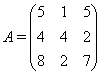
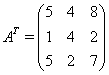
![]()
1.4.3 Определитель матрицы
Поставим каждой матрице по определенному правилу в соответствие число и назовем его определителем матрицы.
Например:
![]()
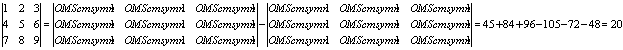
Таким образом вычисляют определители двхмерной и трехмерной матриц. Эта схема вычисления называется мнемоническим правилом. Для четырехмерной матрицы не удобно составлять такие схемы. Существует строгое правило нахождения определителя матрицы n-го порядка. Но мы будем работать только с трехмерными матрицами.
Необходимо обратить внимание на то, что матрица пишется в круглых скобках, а определитель матрицы - в прямых.
Задача 1. Найти определители матриц А и ![]() из Примера.
из Примера.
Обратить внимание, на то что определитель матрицы не совпадает с определителем транспонированной матрицы.
Задача 2. Найти определители матриц.
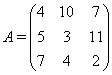
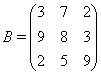
![]()
1.4.4 Домашнее задание
Задача 3. Найти произведение матриц А и В из задачи 2. Вычислить определитель полученной матрицы.
Задача 4. Найти значение выражения ![]() . Матрицы из задачи 2.
. Матрицы из задачи 2.
Необходимо сказать, что последовательность выполнения операций, такая же как и для чисел, но первым выполняют транспонирование.
1.5 Пятый урок
![]()
1.5.1 Проверка домашнего задания
1.5.2 Обратная матрица
Опр. Если ![]() , то
, то ![]() обозначают
обозначают ![]() и пишут
и пишут ![]() .
.
Где ![]() - матрица с единицами на главной диагонали и нулями на остальных местах. Показать главную диагональ.
- матрица с единицами на главной диагонали и нулями на остальных местах. Показать главную диагональ.
Для того, чтобы найти обратную матрицу нам необходимо найти т.н. алгебраическое дополнение.
Пусть дана матрица
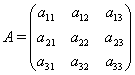
число
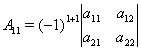
называется алгебраическим дополнением элемента ![]() . Алгебраическое дополнение можно найти для любого элемента матрицы.
. Алгебраическое дополнение можно найти для любого элемента матрицы.
Опр. Алгебраическим дополнением элемента ![]() называется произведение
называется произведение ![]() на определитель матрицы после вычеркивания из нее i-й строки и j-го столбца.
на определитель матрицы после вычеркивания из нее i-й строки и j-го столбца.
Теперь можно найти и обратную матрицу.
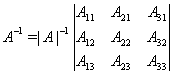
Задача 1. Найти обратную матрицу.
3.5.3 Домашнее задание
Задача 1. Найти обратную матрицу.
1.6 Шестой урок
![]()
1.6.1 Математическая постановка задачи
![]() Итак, имеем две рисковые ц.б., заданные таблицей роста/падения цен и одну безрисковую, заданную процентом годовых. Необходимо сформировать портфель максимальной эффективности.
Итак, имеем две рисковые ц.б., заданные таблицей роста/падения цен и одну безрисковую, заданную процентом годовых. Необходимо сформировать портфель максимальной эффективности.
![]()
Доходность безрисковой ц.б. ![]() .
.
Если сегодня стоимость портфеля ![]() , а через год она окажется равной
, а через год она окажется равной ![]() , то
, то ![]() естественно назвать доходностью портфеля в процентах годовых. Т.е. доходность портфеля - это доходность на единицу стоимости.
естественно назвать доходностью портфеля в процентах годовых. Т.е. доходность портфеля - это доходность на единицу стоимости.
Аналогично доходности всего портфеля находится доходность каждого вида акций. Т.е. нам нужно составить таблицу доходностей для ц.б. первого и второго видов. Например, для ц.б. первого вида доходность за первый год будет ![]() , за второй год -
, за второй год - ![]() . Таким образом находим доходности за все 12 лет для каждого вида акций. Получаем таблицу с двумя столбцами и 11 строками.
. Таким образом находим доходности за все 12 лет для каждого вида акций. Получаем таблицу с двумя столбцами и 11 строками.
Как правило, доходность бумаг колеблется во времени, так что будем считать ее случайной величиной. Найдем среднюю ожидаемую доходность ![]() и среднее квадратичное отклонение
и среднее квадратичное отклонение 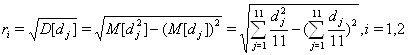 И назовем их соответственно эффективностью и риском i-ой ценной бумаги. Эффективностью портфеля назовем
И назовем их соответственно эффективностью и риском i-ой ценной бумаги. Эффективностью портфеля назовем ![]() . Т.е. математическое ожидание доходности портфеля.А величину
. Т.е. математическое ожидание доходности портфеля.А величину ![]() (1) (где
(1) (где ![]() -ковариация i-ой и j-ой с.в.) назовем риском рисковой части портфеля портфеля.
-ковариация i-ой и j-ой с.в.) назовем риском рисковой части портфеля портфеля.
Обозначим ![]() - доля безрисковой ц.б. в портфеле.
- доля безрисковой ц.б. в портфеле. ![]() - вектор долей первой и второй ц.б.
- вектор долей первой и второй ц.б. ![]() . Тогда естественно, должно выполнятся равенство
. Тогда естественно, должно выполнятся равенство ![]() . Пусть
. Пусть ![]() -ожидаемая эффективность бумаг. V- матрица
-ожидаемая эффективность бумаг. V- матрица ![]() ковариаций ценных бумаг.
ковариаций ценных бумаг. ![]() -риск портфеля.
-риск портфеля.
Используя введенные обозначения, поставим математическую задачу. Как отмечалось выше: ![]() . Если возвести обе части равенства (1) в квадрат и записать в матричной форме, то получим
. Если возвести обе части равенства (1) в квадрат и записать в матричной форме, то получим ![]() . И теперь основное: необходимо добиться максимального значения эффективности портфеля, т.е.
. И теперь основное: необходимо добиться максимального значения эффективности портфеля, т.е. ![]() .
.
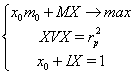
![]()
1.6.2 Решение задачи
![]() Решение задачи найдем по формуле:
Решение задачи найдем по формуле:
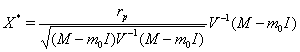 .
.
В результате проделанных операций получим двухмерный вектор - доли рисковых акций в портфеле. Доля безрисковой акции в портфеле найдется из равенства ![]() .
.
Находить решение поставленной задачи удобнее разбив формулу по действиям. Если учащиеся хорошо усвоили предыдущий материал, то вычисления не вызовут ни каких затруднений, т.к. не содержат нового материла.
1.7 Седьмой урок
![]()
Напомнить результаты постановку математической задачи. Записать результ, к которому пришли на прошлом уроке. Продолжить решение.
Доли акций могут оказаться больше 1, или даже отрицательными. Если доля акции отрицательная - необходимо пройзвести операцию short sale. Суть этой операции состоит в следующем: инвестор, формирующий портфель, обязуется через какое-то время поставить бумаги i-го вида (вместе с доходом, который они принесли бы владельцу за это время). За это он сейчас получает их денежный эквивалент. Эти деньги он присоединяет к своему капиталу и покупает рекомендуемые оптимальным решением ц.б. Т.к. ценные бумаги других видов более эффективны, то инвестор оказывается в выигрыше. Можно обойтись и без операции short sale, если инвестору доступны займы денежных средств по безрисковой ставке. Тогда налагают дополнительное условие ![]()
Заключение
![]()
В результате проделанной работы был составлен факультативный курс по теме "Оптимальный портфель ценных бумаг". Он позволяет учащимся профильных экономических классов глубже понять суть работы экономистов, увидеть тесную связь между математикой и экономикой, сделать профессиональный выбор. В ходе факультативных занятий школьники знакомятся с основными понятиями ТВиМС.
Факультатив содержит только необходимые для решения поставленной задачи (формирование оптимального портфеля Тобина максимальной эффективности из предложенных ценных бумаг) понятия. Однако, изученный материал позволяет сформировать у учащихся представление о ТВиМС.
Факультатив расчитан на 10, 11 профильные математические и экономические классы с высоким уровнем успеваимости. Проведенные в 10 экономическом классе МПГ №56 г.Гомеля занятия показали, что школьники способны усаваивать данный материал. Однако время уроков 2-6 необходимо увеличить до 2 академических часов.
Литература
![]()
1. Малыхин В.Н. "Оптимальный портфель и пакеты" м.: ОЛМА-ПРЕСС. 2000
2. Малыхин В.Н. "Финансовая математика" М.: ИНФРА-М, 1999
3. Маршалл Дж. "Финансовая инженерия" М.: ИНФРА-М, 1998
4. Малинковский Ю.В. Лекции по ТВиМС
5. Бузланов А.В. Лекции по алгебре и теории чисел
6. Журнал "Математика в школе", 1975-1985
Похожие работы
... занятий конспект лекций 03.02.97 5. Подготовка письменного отчета 06.02.97-29.02.97 6. Сдача диф. зачета 04.03.97-06.03.97 Общая характеристика базы практики. Педагогическая практика завершает психолго-педагогическую подготовку студентов нашего ВУЗа. Я проходил практику в средней школе № 60 (Зализнычный район города Киева).Школа ...
... является ближайшее, а не дальнейшее значение слова. Таким образом, психологическое направление и особенно младо-грамматизм ответили на многие вопросы, стоявшие перед языкознанием в середине XIX в. Была уточнена методика сравнительно-исторического языкознания, поставлены основные проблемы семасиологии и функционально-семантической грамматики, проанализировано взаимоотношение языка и речи, ...
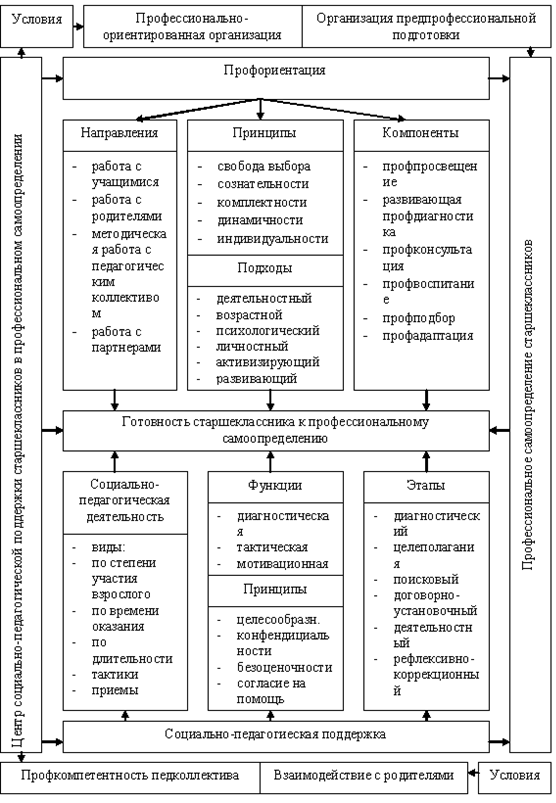
... , целей и задач. С учетом выбранных методов проведем следующий этап опытно-эксперементальной работы. 2.2 Опытно-экспериментальное исследование условий профессионального самоопределения старшеклассников Задачей диагностического этапа является самопознание (индивидуальных особенностей и профессиональной направленности) личности. С помощью методов диагностики происходит дальнейшее развитие ...
... М. Одаренные люди в детстве. // Дошкольное воспитание. 1996. № 9. С.19-22. 3. Берсенева Л., Третьякова Н. Научите детей рисовать. // Дошкольное воспитание. 2004. № 2. С. 70-72. 4. Безруких М.М. Сенсомоторное развитие дошкольников на занятиях по изобразительному искусству. – М., 2001. 186с. 5. Богданова Т.Г. Корнилова Т.В. Диагностика познавательной сферы ребенка. – М.: ...


0 комментариев