См > 8 см

9 см > 8 см

На уроках повторення вивченого матеріалу молодші школярі любили працювати динамічними парами. Заздалегідь були приготовлені картки з двома – трьома практичними завданнями з теми, що вивчалася. Одержавши картку, двоє учнів перше завдання виконували спільно. Один учень пояснював іншому, як потрібно виконувати завдання, другий – слухав, запитував або висловлював своє розуміння. Друге і третє завдання діти виконували самостійно, занотовуючи їх у зошити. Потім перевіряли один одного з відповідним коментуванням допущених помилок. Вчитель при цьому повинен був прослідкувати, щоби хоч один учень правильно розв’язав завдання.

Ці ігри прості, але вони дозволяють в ігровій формі повторити таблиці додавання і віднімання, множення і ділення, а також внести в урок елемент змагання – це сприяє активізації навчальної діяльності учнів.

Часто ми використовували сюжетно-рольові ігри та ігри-драматизації, оскільки вони допомагають учням краще розв’язувати задачі.

Наведемо приклад сюжетно-рольової гри «Магазин».

Матеріал гри: картки із зображеннями різних предметів та записами цін, монети.

Зміст гри: кожний учень має на парті картку і набір монет (заздалегідь приготовлених, які зберігаються у спеціальних коробочках, як роздатковий дидактичний матеріал). Завдання: продати предмети, зображені на картці сусіду по парті, і купити в нього предмети, зображені на його картці. У зошиті треба записати номер карток, монети, якими було заплачено за покупку і які учень одержав під час продажу. Ускладнити гру можна таким чином, щоб монет не вистачило для розрахунку (дати здачу або купити все). Це змусить учня перелічити гроші, перевірити свою покупку і прийти до висновку не вистачає!

Доцільно проводити різні варіанти цієї гри.

Також щоб урок був цікавим і ефективним розв’язувались кросворди за темами уроку чи розділу, ребуси, лабіринти, магічні квадрати та інші цікаві завдання (див.додатки). Ось, наприклад, розв’язати таке цікаве завдання:

Цифри 6, 7, 8, 9, 10, 11, 12, 13, 14 треба розмістити в три рядки один під одним так, щоб сума по рядках, стовпчиках і діагоналях дорівнювала 30.

Для посилення уваги, розвитку мислення та кмітливості, учням пропонувались різноманітні за формою і змістом цікаві запитання й задачі. Ці запитання, загадки й задачі були невеликими, доступними для дітей, з відтінком легкого й розумного гумору (див. додатки).

Наприклад, цікаве запитання:

Оля вийшла з дому до школи на 3 хв раніше від Сергійка, а Сергійко вийшов на 2 хв. пізніше від Катрусі. Хто з дітей вийшов раніше і на скільки хвилин?

Надзвичайно підвищує в учнів інтерес до математики, сприяє розширенню дитячого кругозору та ознайомлює із цікавими математичними фактами – математичний куточок. Він повинен бути в міру яскраво, проте цікаво оформлений, а його матеріал – пов’язаний з програмним матеріалом. Назвали ми його так: «Дізнайся, відгадай, обчисли!» і часто використовували під час уроку. Іноді цікаві математичні факти, головоломки, загадки, задачі-жарти збирали й самі учні. Для збереження матеріалів куточка були заведені папки.

Як бачимо, процес навчання математики в експериментальному класі здійснювався спільною працею вчителя і учнів. У цьому класі ми керувались таким принципом: «Навчання – задоволення! Граючись – навчайся; навчайся, граючись!» [44; 5]. Враховуючи вікові та індивідуальні особливості учнів, ми намагались будувати уроки так, щоб сприйманню теоретичного матеріалу передувало послідовне виконання практичних вправ, репродуктивна діяльність чергувалася з пошуково-творчою, а матеріал, який потребує напруженої уваги, обов’язково був доповнений ігровими формами діяльності. М. Горький писав: «Гра – творчість, гра – праця. Праця – шлях дітей до пізнання світу» [35; 4].

В контрольному класі засвоєння знань з математики відбувалось таким методом: розв’язати якнайбільше прикладів і задач, таким чином виконавши великий обсяг завдань, учні добре оволодіють навчальним матеріалом.

У ході третього етапу експерименту ми провели підсумкову контрольну роботу в експериментальному та контрольному класах. Перше, друге і третє завдання стосувалось суто програмового матеріалу, а четверте – не виходило за межі програми, але мало певні ускладнення у формулюванні.

Наведемо тексти цієї роботи і результати їх виконання.

Завдання 1. Розв’язати приклади:

33 + 47 2 * 7 16 : 2 + 17 61 – 25

55 – 38 12 : 2 3 * (16 – 8 ) 13 + 58

 

Завдання 2. Розв’язати задачу:

Токар виготовив 10 деталей, а його учень виготовив 6 деталей. Всі деталі склали у дві коробки порівну. Скільки деталей в одній коробці?

Завдання 3. Порівняти і поставити потрібний знак:

16 : 2…12 48 + 10…58 27… 3 * 7

Додаткове завдання. Розв’язати задачу:

У коваля було 34 підкови. За день він мав підкувати 9 коней, кожного на 4 ноги. Скільки підків не вистачило ковалю?

Завдання контрольної роботи в першому і другому варіантах були подібніими, тому ми навели зміст завдань одного варіанту.

Результати виконання цих завдань узагальнені в таблицях 3 і 4.

Таблиця 3.

Виконання підсумкових контрольних завдань в експериментальному і контрольному класах

Правильно розв’язали ( у %)
Класи	1-е завдання	2-е завдання	3-є завдання
2 експер.	89	86	85
2 контр.	74	71	73

Таблиця 4. Виконання додаткового завдання в експериментальному і контрольному класах

Правильно розв’язали ( у %)
Класи	Додаткове завдання
2 експер.	68
2 контр.	48

Порівняння результатів контрольної роботи свідчить про те, що в експериментальному класі рівень знань, умінь і навичок з математики в учнів значно вищий, ніж у контрольному. Це можна пояснити тим, що принцип, яким ми керувались в експериментальному класі: «Навчання – задоволення! Граючись – навчайся; навчайся, граючись» справді є ефективним.

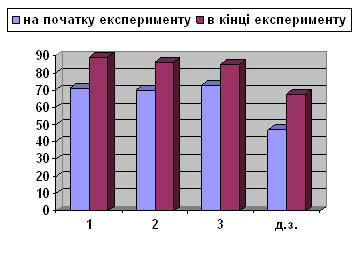
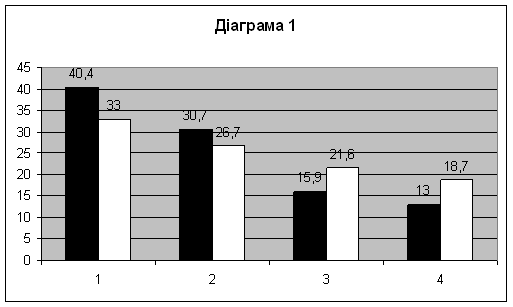
У нижче наведених діаграмах порівнюються результати виконання програмових і додаткових завдань в експериментальному і контрольному класах на початку і в кінці експерименту (діаграми 1, 2).

Діаграма 1. 2 А клас (експериментальний клас)

Правильно виконали (у %)

№ завдання

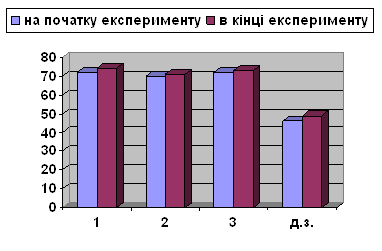
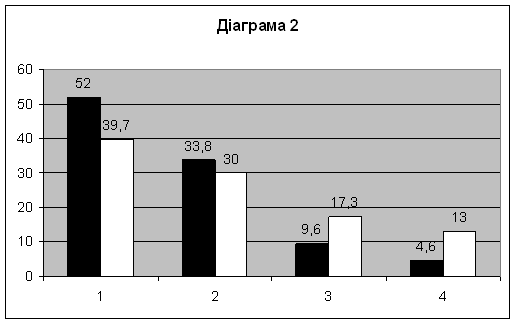
Діаграма 2. 2 Б клас (контрольний клас)

Правильно виконали (у %)

№ завдання

Аналізуючи одержані результати експериментального дослідження можна зробити висновок, що дидактична гра – це ефективний метод навчання математики молодших школярів.

Ігри та ігрові ситуації допомагають учням у навчанні, організовують їх, розвивають, розширюють їхні пізнавальні можливості, виховують. Цілком природно, що саме у грі слід шукати приховані можливості для успішного засвоєння учнями математичних понять, вироблення необхідних умінь і навичок.

Висновки

 

Мета сучасної освіти полягає не стільки в передачі конкретної інформації знань, скільки в сприянні саморозвитку дітей, підготовці їх до майбутнього самостійного життя, активної участі в праці, реалізації своїх можливостей. Для цього кожна дитина повинна отримати якісну освіту. Здобуття знань, умінь і навичок починається ще із дошкільного періоду, проте у молодшому шкільному віці закладається та основа, від якої залежить подальше успішне навчання.

Вивчення математики у початковій школі розвиває уяву, спостережливість, образне й логічне мислення, формуються також особисті якості дитини: зібраність, організованість, здатність швидко і правильно приймати рішення, відстоювати свою думку.

Формування учня самостійною, ініціативною, вдумливою особистістю може бути успішним, якщо потурбуватися про це з першого проведеного уроку. Ефективне засвоєння знань передбачає таку організацію пізнавальної діяльності учнів, за якої навчальний матеріал стає предметом активних розумових і практичний дій кожної дитини. Тому для цього необхідно на уроках використовувати відповідні методи навчання..

Проблема дипломної роботи полягала у дослідженні ефективного впливу методу дидактичної гри на процес навчання математики молодших школярів.

У процесі вивчення даної проблеми розв’язувались завдання, які були поставлені відповідно до мети і гіпотези нашого дослідження:

1. Шляхом аналізу психолого-педагогічної та методичної літератури ми побачили, що проблему використання дидактичних ігор у навчальному процесі досліджували такі філософи, психологи і педагоги, як Я.А. Коменський, Ж-Ж.Руссо, І.Кант, Ж.Піаже, К.Ушинський, А.Макаренко, В.Сухомлинський, А.Сікорський, П.Блонський, Л.Виготський, О.Леонтьєв, Д.Ельконін та інші. Також з’ясували, що дидактичні ігри відповідають природним потребам молодших школярів, оскільки поєднують у собі елементи навчання, прикладної, репродуктивної та творчої діяльності, що дає змогу розвивати емоційну сферу дитини, її пізнавальні інтереси, інтелектуальні та духовні потреби, а вміле використання ігор підвищує навчальну активність учнів, інтенсивність мислення, пам’яті, уваги та уяви.

2. Дидактичні ігри або ігрові ситуації під час вивчення математики в початкових класах можна використовувати на будь-якому етапі уроку. Завдяки ігровому методу до систематичної розумової праці вдається залучити всіх учнів (навіть пасивних), дати їм змогу відчути успіх, повірити в свої сили.

Проте завжди потрібно пам’ятати, що будь-яка дидактична гра ефективною буде лише за певних умов: якщо у ній поєднано два елементи – пізнавальний та ігровий; якщо вирішує певне конкретне завдання, яке під силу її учасникам; дидактичні ігри повинні утворювати систему, яка передбачає їх певну послідовність і поступове ускладнення.

Формами ігрової діяльності учнів на уроці математики можуть бути ігри-вправи, ігри-драматизації, сюжетно-рольові ігри та ігри-конструювання.

3. Для того, щоб дидактична гра ефективно впливала на навчальну діяльність учнів, необхідно дотримуватись відповідних методичних вимог: - ігри мають відповідати навчальній програмі; - ігрові завдання повинні бути не надто легкими, але й не дуже складними; - добирати ігри відповідно до вікових особливостей учнів; - використовувати різноманітні ігри; - до гри залучати всіх учнів класу; - підсумок гри має бути чітким і справедливим.

4. Проведення експериментального дослідження показало, що дидактична гра має ефективний вплив на засвоєння учнями навчального матеріалу з математики. На початку дослідження рівень знань учнів в експериментальному і контрольному класах становив приблизно однаковий відсоток (72%). Проте в експериментальному класі після тривалого використання в навчальному процесі дидактичної гри, знання учнів покращились на 17 %. В контрольному класі проводились традиційні уроки, тому тут рівень навченості зріс лише на 2-3%.

З цього ми зробили висновок, що навчальний матеріал з математики, викладений із використанням ігрових ситуацій, з наступним проведенням практичної роботи чи бесіди (у формі дидактичної гри, або з використанням окремих її елементів) дають набагато кращі результати, ніж традиційна форма викладення матеріалу.

Використовувати дидактичні ігри у навчальному процесі радимо усім педагогам, тому що метою такої гри є ніщо інше, як допомогти малим школярам навчитись планувати свою роботу; організовано працювати; учитись запитувати і відповідати; пізнавати не лише себе, але й інших; аналізуючи, знаходити головне; правильно доводити свою думку; доповнювати, продовжувати, завершувати; учитись порівнювати; іти від причини до наслідку; навчитись контролювати й оцінювати.

Як засвідчує практика, така організація здобуття знань дає змогу максимально активізувати навчально-пізнавальну діяльність учнів на уроках математики і водночас сприяє не тільки підвищенню якості навчання, а й забезпеченню емоційного благополуччя та психологічного комфорту кожній дитині вже з перших днів навчання у школі.

Зазначимо також, що в процесі проведення уроків математики з елементами гри реалізуються ідеї співдружності, змагання, самоуправління, виховання відповідальності кожного за результати своєї праці, а основне – формується мотивація навчальної діяльності й інтерес дітей до математики.

Список використаних джерел

 

1. Андруховець П. Ігрова педагогіка // Завуч. – 2004. – № 1 (187). - С. 6-16.

2. Ващенко Г. Загальні методи навчання: Підручник для педагогів. – К.:, 1997. – С. 366 – 380.

3. Галкін С. Гра – Шлях до впевненості // Шкільний світ. – 2004. – № 47 (217). – С. 4 – 6.

4. Галкін С. Організація ігрової діяльності на уроці // Завуч. – 2004. – № 30 (216). – С. 9 – 12.

5. Герасимчук Н.М., Головна Г.А., Сухіна Л.А. Математичний ярмарок // Початкова школа. – 1994. – №1. – С.16.

6. Губанова О.В., Левкина И.С. Использование игровых приемов на уроках // Начальная школа. – 1997. – №6.

7. Гузь І. Щоб хотілося грати // Шкільний світ. – 2004. – № 46 (270) .-С.13.

8. Державний стандарт початкової загальної освіти // Початкова школа. – 2001. – № 1. – С. 42.

9. Дон О. Дидактичні ігри в навчально-виховному процесі // Шкільний світ. – 2001. – № 35 (115). – С. 2.

10. Дубич К. Місце рольової гри в навчально-виховному процесі // Нова педагогічна думка. – 2003. – № 1-2. – С.12 – 13.

11. Жданов Д. Дидактичні можливості інтелектуальних ігор // Завуч. – 2007. – № 7 (301). – Наша вкладка. – С. 1 – 14.

12. Желюк О., Хмеляр І. Розвиток творчих здібностей учнів // Завуч. – 2005. – № 11 (233). – С. 3-5.

13. Жорник О. Використання дидактичних ігор у навчанні // Рідна школа.- 2000. – № 4. – С. 63 – 64.

14. Жорник О. Формування пізнавальної активності учнів у процесі спільної ігрової діяльності // Рідна школа. – 2000. – № 3. – С. 37 – 39.

15. Жуковська Н. Закріплення і повторення вивченого матеріалу. Урок-подорож з математики // Початкова освіта. – 2005. – № 32 (320). – С. 17 – 18.

16. Закон України «Про освіту» // Освіта. – 1996. – 25 квітня. – С. 4.

17. Івасенко Т. Подорож математичним океаном // Початкова школа. – 2001.– № 1. – С. 56.

18. Ільяницька Л.С. Ігрові проблемні ситуації // Початкова школа. – 1996.– № 9. – С. 27.

19. Кабалевский Д.Б. Воспитание ума і сердца / У зб.: Учение и розвитие младшых школьников. – М.: Просвещение, 1987. – С. 24 – 31.

20. Калмикова Л., Харченко Н. Психолінгвістичні й лінгвометодичні підходи до змісту формування мовленнєвих умінь і навичок міркувати// Початкова школа. – 2003. – № 3. – С. 6 – 8.

21. Каташинська І. Концепція гри у педагогічній системі Ф. Фребеля // Рідна школа. – 2006. – № 8. – С. 62 – 64.

22. Качеровська Т. Методи та форми ігрового проектування як технології навчання // Наука і освіта. – 2004. – № 4-5. – С. 137 – 142.

23.Качеровська Т. Теоретичні основи застосування ігрового проектування у вітчизняній педагогіці: історичний аспект // Вища школа. – 2005. – № 2. – С. 58 – 63.

24. Келлер Г. Бути учнем невдахою – це назавжди? //Початкова школа. – 2003. – № 10. – С.9.

25. Кияниця О.М. Урок математики в 1 класі // Початкова школа. – 1996.- № 11 – С. 26.

26. Кобанова Л.В. Учебные игры как средство повышения эффективности уроков // Начальная школа. – 1992. – №1.

27. Кочина Л., Листопад Н., Шпакова В. Математика // Початкова школа.- 2001. – № 7. – С. 49 – 60.

28. Кочина Л. Математика у першому класі // Початкова школа. – 2001. – № 11.- С. 46 – 47.

29. Крутій В.А. Місце дидактичної гри на уроках в початкових класах // Наука і освіта. – 2001. - № 2-3. – С. 19 – 22.

30. Кукушин В. Ігрові технології на уроках // Відкритий урок. – 2006. – № 6.– С. 3 – 10.

31. Мартиненко С., Хоружа Л. Методи навчання та їх класифікація // Відкритий урок. – січень 2006. – С. 3 – 4, 9.

32. Масловская Т.А. Дидактические игры на уроках математики // Начальная школа. – 1997. – № 2.

33. Машков А. Математична мозаїка // Початкова школа. – 1994.– № 6. – 33 с.

34.Микитинська М.І., Мацько Н.Д. Ігрова діяльність учнів на уроках математики // Початкова школа. – 1980. – № 9. – С. 46 -53.

35. Микитинська М.І., Мацько Н.Д. Математичні ігри в 1 – 3 класах. – Київ: Радянська школа, 1980. – 128 с.

36. Митник О. Пізнавальні завдання для розвитку творчих здібностей особистості // Початкова школа. – 2001. – № 6. – С.14 – 16.

37. Мовчан Л. Розвиток мислення // Початкова школа. – 2003. – № 11. – С.22.

38. Моро М.Г., Пишккало А.М. методика навчання мате6матики в 1- 3 класах. – Київ: Радянська школа, 1979. – С. 71 – 87.

39. Навчання у грі. Збірник статей. – Київ: Вища школа, 1996. – 315 с.

40. Пироженко Л., Пометун О. Гра і не тільки // Завуч.– 2006. – № 7. (265)- Наша вкладка. – С.8 -11.

41. Савченко О.Я. Дидактика початкової школи. – Київ: Абрис, 1997. – С. 215- 221.

42. Саюк В. Ігрові методи та їх дидактичне значення // Рідна школа.- 2001.– № 4. – С.18 – 20.

43. Саюк В. Історико-педагогічний аналіз. Використання гри у навчальному процесі // Рідна школа. – 2005. – № 7. – С. 50 – 52.

44. Система рейтингових ігор у школі // Завуч. – 2005. – № 5 (227).- С. 5-6.

45. Смаглій О. Застосування ігрових ситуацій на уроках математики // Початкова школа. – 2003. – № 7. – С. 20 – 21.

46. Спасов Л. Проблемно-діяльнісна гра. Педагогічні технології // Відкритий урок. – 2005. – № 19-20. – С. 71 – 73.

47. Торбенко Н. Як зробити навчання цікавим? // Початкова освіта. – 2006. – № 11 (347). – С.3.

48. Фіцула М. М. Педагогіка. – Тернопіль: Богдан, 2004. – С. 130 – 142.

49. Шатохіна О. Навчальна гра // Початкова освіта. –1999. –№ 18. – С.1, 4.

50.Штабова Л. Активізація навчально-пізнавальної діяльності першокласників у доцифровий період навчання математики // Початкова школа. – 2001. – № 9. – С. 38.

51. Штабова Л. Вправи для тренінгу мислення молодших школярів // Початкова школа. – 2003. – № 5.- С. 15.

52. Щербань П. Дидактичні ігри у навчально-виховному процесі // Початкова школа. – 1997. – № 9. – С. 18 – 20.

53. Якиляшек В. Уроки математики з елементами гри // Початкова школа.- 1997. – № 6. – С. 22 – 23.

Додатки

 

Урок-подорож з математики у 2 класі на закріплення і повторення вивченого матеріалу

 

Тема. Закріплення додавання і віднімання двоцифрових чисел з переходом через десяток

Мета. Закріпити вміння додавати і вінімати двоцифрові числа з переходом через десяток у процесі розв’язування прикладів і задач; вправляти у знаходженні числових значень буквених виразів; розвивати кмітливість, уважність, логічне мислення; виховувати бережливе ставлення до природи.

Обладнання. Малюнок корабля, квитки, рибки, пальми, круги.

Хід уроку

І. Організаційний момент.

- Діти, сьогодні у нас буде незвичайний урок. Ми вирушаємо в подорож водними просторами Математичного океану.

ІІ. Повідомлення теми і мети уроку.

- Якщо ви правильно і швидко виконаєте запропоновані завдання, ми побуваємо у різних портах і повернемось додому.

- На нашому кораблі «Математика» є каюти 1-го і 2-го класу. Хто в якій каюті подорожуватиме – ви дізнаєтесь, розв’язавши завдання на квитку.

(Діти отримують по 2 квитки із завданнями. Квиток 1-го класу містить завдання – розв’язати задачу, 2-го класу – приклади. Кожен учень вибирає собі квиток із тим завданням, яке йому під силу розв’язати).

ІІІ. Основна частина – подорож.

- Розселяємось по каютах. Уявіть, що ми йдемо коридором. Я бачу номери кают. Капітан живе у каюті, яка знаходиться між каютами № 39 і 41. У якому номері живе капітан?

- Виглянемо в ілюмінатор. Парами пропливають рибки. Порахуймо їх, починаючи від 36-ї до 58-ї.

- Поблизу з’явилась акула, і рибки, щоб їм не було страшно згрупувались по 5 і по 10. Порахуймо спочатку п’ятірками, потім десятками.

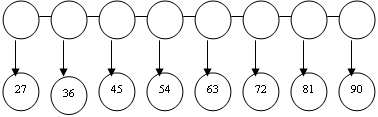
- А зараз, рибки пропонують нам виконати математичний диктант для того, щоб дізнатись, де буде наша перша зупинка.

- Знайдіть суму чисел 25 і 9; 41 зменшіть на 8; перший доданок 55, другий – 0, третій - 6; зменшуване 23, від’ємник 10, знайдіть різницю; знайдіть суму чисел 18 і 7; 33 зменшити на 4; до 47 додати 8; знайдіть різницю 26 і 9.

(Після виконання математичного диктанту, один учень виходить до дошки і по-порядку зачитує отримані відповіді, другий учень знаходить їх на рибці і в такому ж порядку з’єднує прямими лініями)

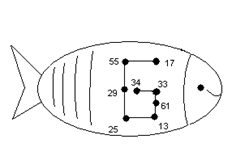
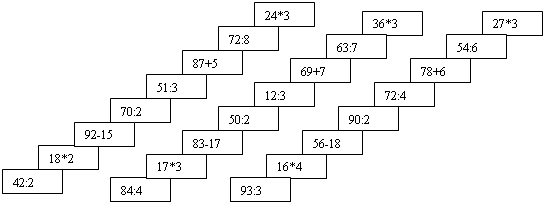
- Що отримали? (Букву Б). Перша зупинка у бухті Обчислень. Виходимо на берег. Перед нами – велетенська пальма. Хочеться забратися на неї? Але для цього потрібно розв’язати приклади.

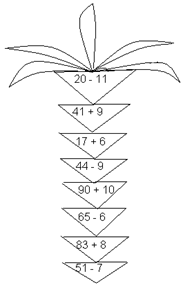
- Забралися на велетенську пальму? Погойдалися на ній? Тоді, мандруємо далі.

- А ось і маленька пальма, на ній математичне завдання: 17 + а. Що це? Доберіть значення а, щоб додавання було без переходу через десяток і з переходом через десяток.

- зараз повернемося до своїх кают і відпочинемо.

Фізкультхвилинка.

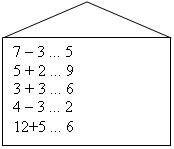
- Поки ми відпочивали наш пароплав підійшов до гавані. Я навіть бачу її назву – Задачна. А тут – схема. Ви можете розтлумачити, що це? Отже, наше завдання – скласти задачу до схеми і розв’язати її.

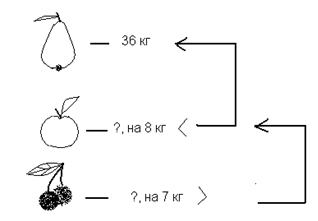
- Наша подорож добігає до завершення. На обрії видніється остання пристань Міркуюча. Я кину кожному круг, щоб він міг самостійно дістатися до берега.

(Діти отримують круги із завданнями. Наводимо приклад одного такого круга)

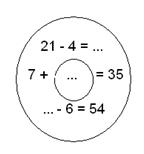
ІV. Підсумок уроку.

- Чи сподобався вам сьогодні урок? Чим саме? А що найбільше сподобалось?

- Поділіться своїми враженнями.

Цікаві задачі й завдання для математичного куточка

1. На полиці стоїть 15 книжок. Якою по порядку буде сьома книжка в ряді, якщо рахувати справа наліво?

2. Кавун важить 2 кг та ще стільки ж. Скільки важить його половина?

3. Скільки років Кості, якщо, коли до його років додати ще 8 і ще 1, то буде 20?

4. Трійка коней пробігла 12 км. Скільки кілометрів пробіг кожен кінь?

5. На двох деревах сиділи горобці. З першого дерева полетів 1 горобець, а потім з другого дерева на перше перелетіло 3 горобці. Після цього на кожному дереві стало по 5 горобців. Скільки горобців було на кожному дереві спочатку?

6. Одне яйце можна зварити за 7 хвилин. За який час можна зварити 5 таких яєць?

7. У двох дівчаток є 9 цукерок. У Люсі в 2 рази більше, ніж у Юлі. Скільки цукерок у кожної з них?

8. Два рибалки ловили рибу і піймали разом 28 окунів і карасів. Коли стали ділити, то виявилося, що один окунь залишився зайвим, а карасів виявилось стільки, скільки окунів в одній купці. Скільки всього окунів і карасів піймали рибалки?

9. Якщо двоє дітей візьмуть по 3 горіхи, то один залишиться, а якщо по 4, то одного горіха не вистачить. Скільки всього було горіхів?

10. Що важче: 1 кг пуху чи 1 кг заліза?

11. На яке найменше число ділиться без остачі будь-яке число?

12. Поставити між 5 і 6 такий знак, щоб результат був більший від 5, але менший від 6?

13. Запиши число 24 трьома однаковими цифрами, крім 8.

14. Запиши число 21 чотирма двійками.

15. Запиши число 100, використовуючи шість раз одну й ту саму цифру.

16. Знайди пропущені числа. Обчисли.

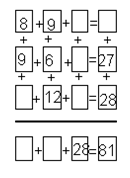
17. Перестав числа так, щоб сума чисел в середніх чотирьох квадратах і в тих чотирьох квадратах, що навколо них, дорівнювала 18.

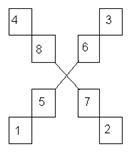
18. Розгадай ребуси:

	40а
			100вппп		7’я

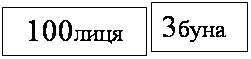19. Знайди вихід із крутих лабіринтів:

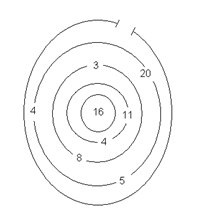
Пройди у кожному крузі лише через один прохід. Виконай над числами такі дії, щоб потрапивши до центра, дістати числа 16 або 45.

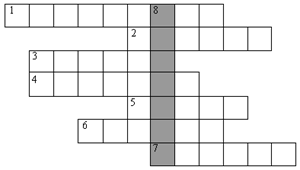
20. Розгадайте кросворд: 1. Як називається другий компонент дії множення? 2. Учні пишуть його і на уроках української мови, і на уроках математики. Це… ? 3. Як називається фігура, у якої є чотири кути і чотири рівні сторони? 4. 25 + 7 – це додавання з переходом через …? 5. Назвіть компоненти дії додавання: доданок, доданок, … 6. Яку назву має таке завдання: Одна книжка коштує 5 грн, а друна – на 3 грн дорожча. Скільки коштують дві книижки разом? 7. Якщо в одному ящику 38 кг картоплі, а в другому – 25 кг, то яку потрібно виконати дію, щоб дізнатись, на скільки більше кілограм картоплі в першому ящику? 8. Виберіть правильну відповідь: 7 – це … (число, цифра). 9. Як називається відсутній компонент дії віднімання: 34 - … = 29 ? 10. Вона цікава, розважальна і навчальна. Це…?

Розгадавши кросворд, прочитайте по вертикалі слово, яке є назвою нашого кросворду.

21.Заповни магічний квадрат числами так, щоб суми чисел, які стоять у будь-якому горизонтальному або вертикальному ряді, а також на будь-якій діагоналі квадрата, дорівнювали одному й тому самому числу, наприклад 15.

 

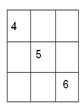
22. Визнач закономірність запису чисел кожного ряду і запиши в кожному ряді ще по 2 – 3 числа: 3, 6, 9, 12, … 4, 8, 10, 20, 22, 44, …

6, 12, 18, 24, … 3, 4, 6, 9, 13, 18,