Навигация
Якщо A [i] - вузол дерева і i > 1,то A [i mod 2] - вузол - “батько" вузла A [i] ;
4. Якщо A [i] - вузол дерева і i > 1,то A [i mod 2] - вузол - “батько" вузла A [i] ;
Приклад: Нехай
A = [45 13 24 31 11 28 49 40 19 27]
- масив. Відповідне йому дерево має вид:
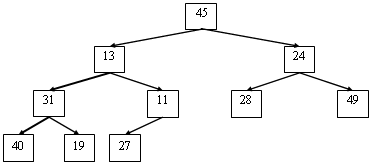
Зверніть увагу на те, що всі рівні дерева, за винятком останнього, цілком заповнені, останній рівень заповнений ліворуч і індексація елементів масиву здійснюється вниз і праворуч. Тому дерево упорядкованого масиву відповідає наступним властивостям:
A [i] (A [2*i], A [i] (A [2*i+1], A [2*i] (A [2*i+1].
Як це не дивно, алгоритм HeapSort спочатку будує дерево, що відповідає прямо протилежним співвідношенням:
A [i] ³ A [2*i], A [i] ³ A [2*i+1]
а потім змінює місцями A [1] (найбільший елемент) і A [n].
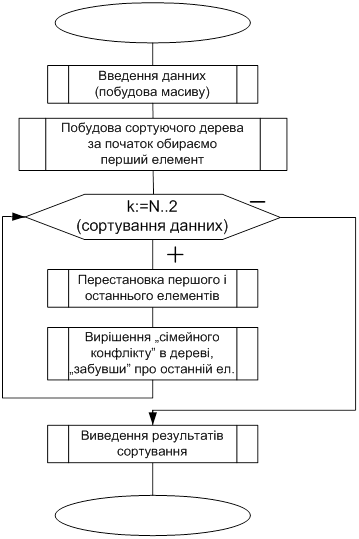
Як і TreeSort, алгоритм HeapSort працює в два етапи:
I. Побудова сортуючого дерева;
II. Просівання елементів по сортуючому дереву.
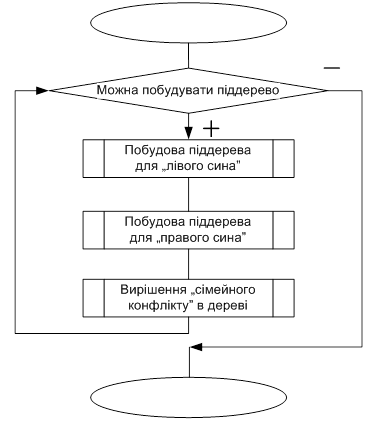
Дерево, що представляє масив, називається сортуючим, якщо виконуються умови (6). Якщо для деякого i ця умова не виконується, будемо говорити, що має місце (сімейний) конфлікт у трикутнику i.
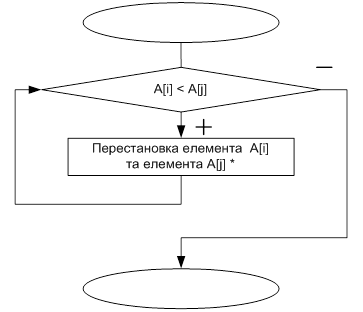
Як на I-ом, так і на II-ому етапах елементарна дія алгоритму полягає в вирішенні сімейного конфлікту: якщо найбільший із синів більше, ніж батько, то переставляються батько і цей син (процедура ConSwap).
У результаті перестановки може виникнути новий конфлікт у тому трикутнику, куди переставлений батько. У такий спосіб можна говорити про конфлікт (роду) у піддереві з коренем у вершині i. Конфлікт роду вирішується послідовним вирішенням сімейних конфліктів проходом по дереву вниз. (На мал шлях вирішення конфлікту роду у вершині 2 відзначений). Конфлікт роду вирішено, якщо прохід закінчився (i > n div 2), або ж в результаті перестановки не виник новий сімейний конфлікт.
I етап - побудова сортуючого дерева - оформимо у виді рекурсивної процедури, використовуючи визначення:
Якщо ліве і праве піддерева T (2i) і T (2i+1) дерева T (i) є сортуючими, то для перебудови T (i) необхідно вирішити конфлікт роду в цьому дереві.
На II-ом етапі - етапі просівання - для k від n до 2 повторюються наступні дії:
1. Переставити A [1] і A [k] ;
2. Побудувати сортуюче дерево початкового відрізка масиву A [1. k-1], усунувши конфлікт роду в корені A [1]. Відзначимо, що 2-а дія вимагає введення в процедуру Conflict параметра k.
Нескладно підрахувати, що
С (n) = O (n log2 n), М (n) = O (n log2 n)
4. Алгоритм програми
Записи R1. Rn вміщені в масиві. Сортування здійснюється за таким спільним алгоритмом:
1. Встановити l= [N/2] +1, r=n
2. Якщо l>1, то зменшити його на 1, R=R1. (Якщо l=1, це означає,що процес сортування завершено). Інакше встановити R=Rr, Rr=R1, r=r-1. Якщо r=1, то встановити R1=R і завершити роботу.
3. Приготуватися до перестановок (j=l)
4. Встановити i=j та j=j*2. Якщо j<r, то перейти в п.5, якщо j=r, то перейти до п.6, інакше - до п.8.
5. Якщо Kj>Kj+1, то j=j+1
6. Якщо К>Кj, то перейти до п.8.
7. Ri=Rj, перейти до п.4.
8. Ri=R, повернутися до п.2.
5. Реалізація програми
Після запуску програма зчитує з вхідного файла байти для сортування. Після цього викликається процедура sort_start, яка запускає процес сортування. При сортуванні використовується рекурсивний алгоритм виклику функцій sorttree, conflict та conswap. При сортуванні інформація записується в потрібне місце масиву згідно описаного вище алгоритму.
Після закінчення сортування програма створює вихідний файл і записує в нього відсортований масив.
6. Системні вимоги
Операційна системаDOS
CPUINTEL 8086 або ст.
RAM640 K
VIDEOCGA або старший
7. Інструкція для користувачаПеред запуском програми треба відредагувати або створити файл piramid. dat. Він у кожному байті (до 255) може містити 1-байтні числа. Для редагування зручно, наприклад, користуватися редактором VC у HEX-режимі.
Після цього треба запустити файл piramid,com. Після її роботи, якщо не виникне помилок, з’явиться файл piramid. out, який буде містити ті ж байти, що і вхідний, але у відсортованому порядку.
Висновки
Отже, ми розглянули як працює алгоритм пірамідального сортування і спробували визначити його складність.
Застосування того чи іншого алгоритму сортування для вирішення конкретної задачі є досить складною проблемою, вирішення якої потребує не лише досконалого володіння саме цим алгоритмом, але й всебічного розглядання того чи іншого алгоритму, тобто визначення усіх його переваг і недоліків.
Звичайно, необхідність застосування саме швидких алгоритмів сортування очевидна. Адже прості алгоритми сортування не дають бажаної ефективності в роботі програми. Але завжди треба пам’ятати й про те, що кожний швидкий алгоритм сортування поряд із своїми перевагами може містити і деякі недоліки.
Розглядаючи такий швидкий алгоритм сортування, як пірамідальне сортування, можна зазначити, що цей алгоритм ефективний, адже він сортує “на місці", тобто він не потребує додаткових масивів. Крім того, цей алгоритм оптимальний: його складність співпадає з нижньою оцінкою задачі, тобто за критеріями C (n) та M (n) він має складність O (n log2 n), але містить складний елемент в умові. Тобто, в умові A [left] має бути строго менше ніж x, а A [right] - строго більше за x. Якщо ж замість “строго більше” та “строго менше" поставити знаки, що позначають “більше, або дорівнює” та “менше, або дорівнює", то індекси left і right пробіжать увесь масив і побіжать далі. Вийти з цієї ситуації можна було б шляхом ускладнення умов продовження перегляду, але це б погіршило ефективність програми.
Отже, головною задачею, яку має вирішити людина, яка повинна розв’язати задачу сортування - це визначення як позитивних, так і усіх негативних характеристик різних алгоритмів сортування, передбачення кінцевого результату. До того ж, треба враховувати головне - чи, можливо, цю задачу задовольнить один з класичних простих алгоритмів сортування.
Використана література1. Львов М.С., Співаковський О.В. Основи алгоритмізації та програмування. - Херсон, 1997.
2. Д. Кнут. Искусство программирования ЭВМ: Т.3. Сортировка и поиск. М., МИР, 1978.
Додаток Лістинг програми
.286
. model tiny
. code
org 100h
start:
jmp begin
n db?
a db 0,255 dup (?)
; si=i; di=j
conswap proc near
pusha
mov al,byte ptr a [si]
mov bl,byte ptr a [di]
cmp al,bl
jae con_sk
mov byte ptr a [si],bl
mov byte ptr a [di],al
con_sk:
popa
retn
conswap endp
conflict proc near
push bp
mov bp,sp
pusha
mov ax, [bp+4] ; i
mov bx, [bp+6] ; k
; j=dx
mov dx,ax
shl dx,1; j=i*2
cmp dx,bx
ja conf_stop; j>k
cmp dx,bx
jb conf_1
; j=k
; conswap (i,j)
mov si,ax
mov di,dx
call conswap
jmp conf_stop
; j<k
conf_1:
push ax
mov si,dx
mov ah,byte ptr a [si+1]
mov al,byte ptr a [si]
cmp ah,al
jbe sk_2
inc dx
sk_2:
pop ax
; if (a [j+1] >a [j]) j++;
; conswap (i,j)
mov si,ax
mov di,dx
call conswap
; conflict (j,k);
push bx
push dx
call conflict
pop dx
pop bx
conf_stop:
popa
pop bp
retn
conflict endp
sorttree proc near
push bp
mov bp,sp
pusha
mov ax, [bp+4] ; i
mov bl,n
xor bh,bh; n
shr bx,1
cmp ax,bx; i<n
jae sort_exit
; sorttree (2*i)
mov bx,ax
shl bx,1
push bx
call sorttree
pop bx
; sorttree (2*i)
mov bx,ax
shl bx,1
inc bx
push bx
call sorttree
pop bx
; conflict (i,n)
mov bl,n
xor bh,bh
push bx
push ax
call conflict
pop ax
pop bx
sort_exit:
popa
pop bp
retn
sorttree endp
start_sort proc
mov ax,1
push ax
call sorttree
pop ax
mov cl,n
mov ch,0
inc cx
lo:
; conswap (k,1)
mov si,cx
mov di,1
call conswap
; conflict (1,k-1)
mov bx,cx
dec bx
push bx
push ax
call conflict
pop ax
pop bx
dec cx
cmp cx,1
jne lo
ret
start_sort endp
in_file db 'piramid. dat',0
out_file db 'piramid. out',0
errm db 'File error$'
begin:
; вiдкрити вхiдний файл
mov ah,3dh
mov al,0
mov dx,offset in_file
int 21h
jc err_file
mov si,ax; handle
; read
mov ah,3fh
mov bx,si
mov cx,255
mov dx,offset a+1
int 21h
mov n,al
; close
mov ah,3eh
mov bx,si
int 21h
call start_sort
; creat
mov ah,3ch
xor cx,cx
mov dx,offset out_file
int 21h
mov si,ax
; write
mov ah,40h
mov bx,si
mov cl,n
mov ch,0
mov dx,offset a+1
int 21h
; close
mov ah,3eh
mov bx,si
int 21h
. exit 0
err_file:
mov ah,9
mov dx,offset errm
int 21h
. exit 0
end start
Похожие работы
... іб руху по дереву від кореня до листків. Рух вгору задається правилом 4: 4. Якщо A[i] - вузол дерева та i > 1, то A[i mod 2] - вузол - “батько” вузла A[i]; Вхідні – вихідні дані Для роботи з даною програмою та алгоритму пірамідального сортування взагалі, нам необхідно ввести елементи масиву визначеної довжини, який необхідно відсортувати. В результаті роботи програми ми отримаємо ві ...
... сортування включенням; - сортування вибором; - сортування обміном. У курсовій роботі ми детально розглянемо швидкі алгоритми сортування елементів масиву, проведемо їх порівняльний аналіз. Крім цього, розглянемо і прямі методи сортування, їх позитиви і недоліки, що дасть змогу краще визначити ефективність і складність швидких алгоритмів сортування. Розділ І. Прямі методи сортування масивів ...
... оцінка складності алгоритму - О(n*log(n)). Даний алгоритм має сенс застосування лише на великих обсягах даних від 500-1000 елементів. Тільки в цьому випадку можна побачити виграш алгоритму в ефективності. Для менших обсягів даних він малопридатний. 3 Синтез машини Тьюрінга 3.1 Загальні відомості Машина Тьюрінга - це кінцевий автомат, забезпечений безкінченою стрічкою і читаючою/записуючою голівкою ...
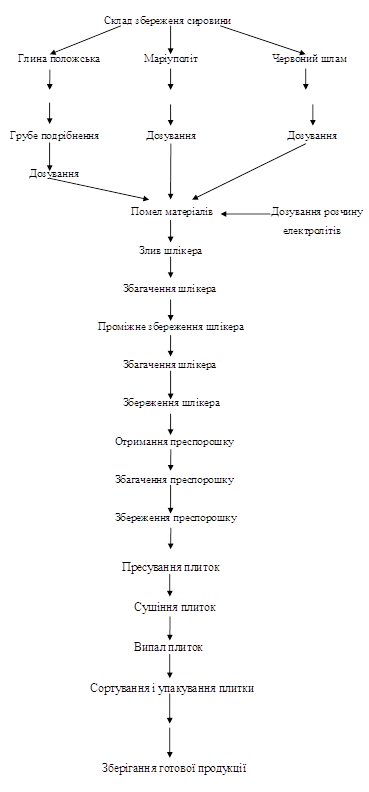
... ; 11 - канал конвеєра; 12 - відкрита частина конвеєра; 13,14,15 - вентилятори; 16 - теплообмінник Рисунок 2.6 - Потоково-конвеєрна лінія Буде встановлено 2 потоково-конвеєрних ліній для виробництва плиток для підлоги продуктивністю 400 тис м²/рік. 2.5.11 Розрахунок складу готової продукції При розрахунку складу готової продукції необхідно знати запас виробів, вид упаковки, площу, що ...

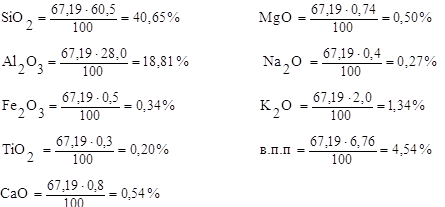
0 комментариев