Навигация
2.2 Завдання 1.2
Варіант 30
Перетворити модель, задану у виді системи нелінійних рівнянь до виду f 1(x) = y і f 2 (y)= x. Побудувати їхні графіки і визначити початкове наближення рішення. Вирішити систему нелінійних рівнянь.
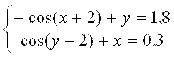
Необхідно знайти інтервали значень функції для x та y таким образом:
Інтервал значень y:
-cos(x+2)+y=1.8
cos(x+2) = y-1.8
-1≤y-1.8≤1
0.8≤y≥2.8
Інтервал значень x:
cos(y-2)+x=0.3
cos(y-2)=0.3-x
-1≤0.3-x≤1
-1.3≤-x≤0.7
-0.7≤x≤1.3
Рішення засобами Excel.
Дану систему рівнянь можливо вирішити використовуючи команду «Пошук рішення».
Заносимо початкові данні у програму Excel (рис.2.9):

Рисунок 2.9 – Таблиця початкових даних
Для перевірки правильності введення формул необхідно включити режим відображення формул (рис.2.10):

Рисунок 2.10 - Дані в режимі відображення формул
Вікно «Пошук рішення» необхідно заповнити наступним чином (рис.2.11):

Рисунок 2.11 – Вікно пошуку рішень
Після виконання команди «Пошук рішення» ми побачимо результат обчислень (рис.2.12):

Рисунок 2.12 – Вікно з рішеннями
Виходячи із отриманих даних необхідно побудувати графік функції (рис.2.13):
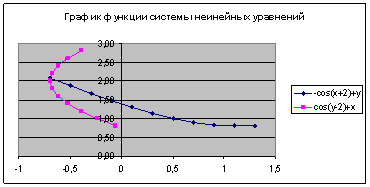
Рисунок 2.13 – Графік функції системи нелінійних рівнянь
Результат:
x= -0.698, y= 2.065
Рішення засобами MathCAD
Рішення даної системи рівняння можна знайти за допомогою розв'язуваного блоку Given...Find.
Задамо початкові значення:
![]()
З використанням функції Find знаходимо точне рішення системи рівнянь.
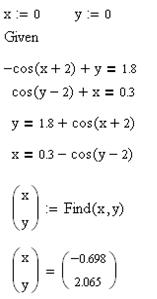
Рисунок 2.14 – Рішення системи нелінійних рівнянь
Результат: x= -0.698; y= 2.065
Перевірка:
Щоб перевірити отримані значення підставляємо їх в дану систему рівнянь.
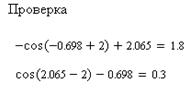
Рисунок 2.15 – Перевірка рішення системи нелінійних рівнянь
Рішення даної системи рівнянь було знайдено у декілька способів, за допомогою MS Excel та MathCAD, отриманні результати є однаковими, але методи які використовуються у цих програмах відрізняються.
2.3 Завдання
Задача А. Вирішити задачу проектування конусоподібного фільтра.
З круглої заготівлі (r = 2) фільтрованого паперу вирізають сектор з кутом θ, потім з іншого роблять фільтр у виді конуса. Необхідно розрахувати величину кута θ, при якій забезпечується максимальний обсяг конуса (рис.2.10).
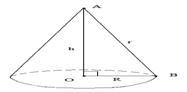
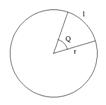 R – радіус основи конуса; h – висота конуса; r – радіус заготівлі фільтрованого папера.
R – радіус основи конуса; h – висота конуса; r – радіус заготівлі фільтрованого папера.
Рисунок 2.16 – Окружність та конус
![]() – довжина
– довжина
![]() – формула для куска дуги
– формула для куска дуги
Знаходимо різницю ![]()
![]()
У конусі получили прямокутний трикутник АОВ, кут О = 90о, h – катет у прямокутному трикутнику. Для знаходження катетів обчислимо корінь із різниці гіпотенузи r та катета R.
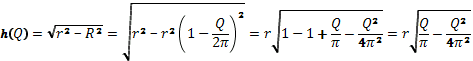
![]()
![]()
Цільова функція має вид: ![]()
Обмеження: ![]()
Розв’язання засобами Excel

Рисунок 2.17 – Розв’язання в Excel
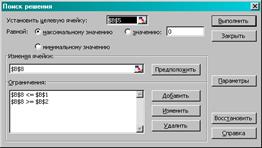
Рисунок 2.18 – Пошук рішення
Необхідний кут θ дорівнює 66 градусів.
Рішення засобами MathCAD
Для рішення у MathCAD необхідно задатися початковими значеннями:
![]()
З використанням функції Maximize знаходимо оптимальний обсяг конуса.
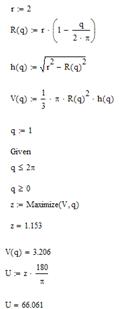
Рисунок 2.19 – Розв’язання в MathCAD
Результат: кут θ дорівнює 66 градусів.
Дане рівняння вирішили різними методами й засобами в результаті одержали однакові відповіді, але методи рішення відрізняються. Тому що за допомогою програми MathCAD неможливо зрозуміти процес рішення задачі, що дозволяє зробити MS Excel.
Задача Б. Проектування 2 -х конусоподібних (пожежних) ребер.
З круглої заготівлі жерсті (r = 3) вирізають сектор з кутом ![]() , потім з іншого роблять цебро у виді конуса і з вирізаного сектора теж (тобто 2-а цебра) (рис.2.20).
, потім з іншого роблять цебро у виді конуса і з вирізаного сектора теж (тобто 2-а цебра) (рис.2.20).
Необхідно розрахувати величину кута ![]() , тобто як необхідно розкроїти заготівлю, щоб обсяг 2-х цебер був максимальним.
, тобто як необхідно розкроїти заготівлю, щоб обсяг 2-х цебер був максимальним.
R – радіус основи конуса; h – висота конуса; r – радіус заготівлі.

Рисунок 2.20 – Окружність, велика заготівля, маленька заготівля
Формули для знаходження радіусу R, висоти h та обсягу V великої заготівлі:
![]()
![]()
![]()
Формули для знаходження радіусу R, висоти h та обсягу V маленької заготівлі:
![]()
![]()
![]()
Цільова функція має вид:
![]()
Обмеження: ![]()
Розв’язання засобами Excel
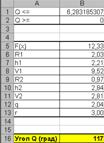
Рисунок 2.21 – Розв’язання в Excel
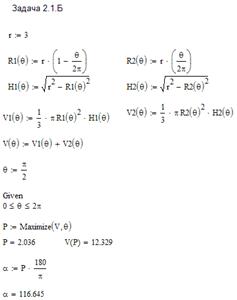
Рисунок 2.22– Розв’язання в MathCAD
Результат: кут θ дорівнює приблизно 117 градусів.
Пошук рішення даної задачі був виконаний з використанням різних програм та методів рішення, але результати обчислень є однаковими.
Задача 15. При яких розмірах прямокутного басейну даної місткості V(x,y,z) = 220м3 на облицювання його стін і дна буде потрібно найменша кількість матеріалу, тобто мінімум S(x,y).
Заносимо початкові в таблицю (рис.2.23):

Рисунок 2.23– Таблиця початкових даних
Для перевірки правильності введення формул необхідно включити режим відображення формул (рис.2.24):

Рисунок 2.24– Дані в режимі відображення формул
Вікно «Пошук рішення» необхідно заповнити наступним чином (рис.2.25):

Рисунок 2.25– Вікно пошуку рішень

Рисунок 2.26– Вікно з рішеннями
Рішення рівняння за допомогою MathCad
Так як наша задача полягає у знаходження мінімальної кількості матеріалу для виготовлення ємності, ми скористуємося функцією Minimize.
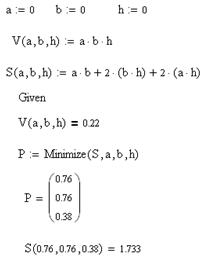
Рисунок 2.27 – Рішення задачі засобами MathCAD
Результат: a=0,76; b=0.76; h=0.38; S=0.1733.
Похожие работы
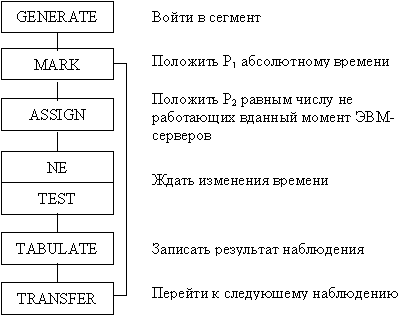
... , визначення основних характеристик одноканальних систем масового обслуговування вимагає великої обчислювальної роботи, в зв’язку з чим всі розрахунки робляться на комп’ютері. 1.2 Побудова моделей задач масового обслуговування (на прикладі роботи обчислювального центру (ОЦ)) 1.2.1 Модель для імітації виробничої діяльності ОЦ 1.2.1.1 Завдання Розробити модель для імітації виробничої ді ...
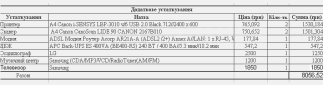
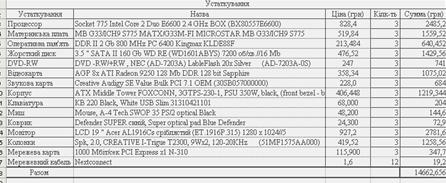
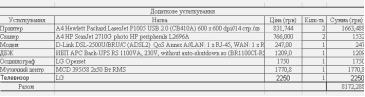
... 1.2 8 Завдання 2.1 (А,Б, варіант) Ємність для поливу газона 7 Завдання 2.2 27 1.2 Опис призначення офісу і його програмне забезпечення Ця установа призначена для роботи в сфері видавництва, необхідні наступні кадри: головний редактор, 2 оператори ПК, секретар. Офіс може виконувати: o Створення учбової, учбово-методичної літератури, яка відповідає потребам державних стандартів осв ...
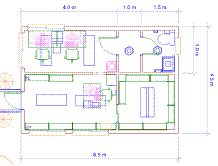
... проектування. СИСТМЕМА АВТОМАТИЗОВАННОГО ПРОЕКТУВАННЯ, ГРАФІЧНЕ МОДЕЛЮВАННЯ, МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ, ОПТИМІЗАЦІЯ, ОПТИМАЛЬНІСТЬ. ЗМІСТ ВСТУП 1. ГРАФІЧНЕ МОДЕЛЮВАННЯ ОФІСУ МОБІЛЬНОГО ЗВ’ЯЗКУ 1.1 Початкові дані для проектування офісу 1.2 Опис призначення офісу та його програмне забезпечення 1.3 Співробітники офісу 1.4 Альтернативне комп'ютерне устаткування 1.5 План офісу та його ...
... Висновки по розділу 3 У даному розділі диплома була розроблена автоматизована інформаційна система розрахунку прибутку на гірничо-збагачувальному підприємстві. Дана система була розроблена для підвищення ефективності роботи підприємства. В основу алгоритмів обробки даних покладені методи математичної статистики й оптимізаційні моделі. Для проектування і реалізації автоматизованої інформаційної ...












0 комментариев