Ректификация

Санкт-Петербургский государственный технологический институт.

Кафедра процессов и аппаратов

Курсовой проект

на тему: Ректификация

Выполнил:

Проверил: .

2008 г.

Задание по курсовому проектированию N 34-01

Спроектировать ректификационную установку для непрерывного разделения смеси: ацетон-метиловый спирт под атмосферным давлением. Сделать подробный расчет ректификационной колонны и водяного подогревателя исходной смеси. Куб-испаритель, дефлегматор, холодильник кубового остатка и холодильник дистиллята рассчитать приближенно, используя коэффициенты теплопередачи из “Примеров и задач…". Выбрать стандартные аппараты. Сделать чертеж общего вида подогревателя исходной смеси и эскиз технологической схемы.

Исходные данные для расчета

Колонна насадочная

Производительность установки по исходной смеси 6.6 т/час.

Концентрация легколетучего компонента в исходной смеси 30%масс.

Концентрация легколетучего компонента в дистилляте 80%масс.

Концентрация легколетучего компонента в кубовом остатке 2%масс.

Температура исходной смеси 10⁰С.

Начальная температура охлаждающего воздуха 10⁰С.

Готовые продукты охлаждаются до 30⁰С.

Температура греющей воды меняется от 98 до 70 ⁰С.

Дата выдачи задания 12 февраля 2008 г.

Руководитель курсового проекта, Ст. преподаватель, к. т. н.

Студент

Содержание

Введение

1. Технологические расчеты

1.1 Расчет ректификационной колонны

1.1.1 Материальный баланс колонны

1.1.2 Определение массовых и объёмных расходов пара и жидкости

1.1.3 Гидравлический расчет колонны

1.1.3.1 Определение рабочей скорости пара

1.1.3.2 Определение диаметра колонны и плотности орошения

1.1.3.3 Гидравлическое сопротивление 1 м насадки

1.1.3.4 Определение активной поверхности насадки

1.1.4 Расчет высоты колонны

1.1.5 Тепловой баланс ректификационной колонны

1.2 Расчет теплообменных аппаратов, входящих в общую схему работы ректификационной колонны

1.2.1 Расчет теплообменного аппарата для подогрева исходной смеси водой

1.2.2 Расчет конденсатора-дефлегматора

1.2.3 Расчет куба-испарителя.

1.2.4 Расчет холодильников для охлаждения продуктов ректификации

Вывод

Список литературы

Приложения

 

Введение

В химической, нефтехимической, фармацевтической, пищевой и других отраслях промышленности часто возникает необходимость разделить смеси двух или большего числа жидкостей на отдельные составляющие. Наиболее характерным примером является разделение нефтепродуктов на отдельные фракции, обладающие различными летучестями.

Процесс разделения основан на том, что все жидкости, составляющие смеси, имеют разные летучести или, иначе говоря, - разные температуры кипения при одинаковом внешнем давлении. Следствием такого свойства жидкостей является различное количество паров компонентов над жидкой смесью. Пары над смесью оказываются обогащенными парами более летучих компонентов. Если смесь таких паров отделить от жидкой фазы и полностью сконденсировать, то состав полученного конденсата будет таким же, что и состав паров. Следовательно, новая жидкая смесь окажется в большей степени обогащенной относительно более летучим компонентом по сравнению с исходной жидкой смесью.

Для этого широко применяют ректификацию, которая осуществляется в аппаратах, называемых ректификационными колоннами. Они бывают с непрерывным контактом фаз - насадочные колонны, и со ступенчатым контактом фаз - аппараты тарельчатого типа (с колпачковыми, ситчатыми, клапанными и решетчатыми тарелками).

Основной объем насадочной колонны заполняется беспорядочно насыпанной дисперсной насадкой, т.е. твердым материалом, химически инертным по отношению к обеим фазам и к целевому компоненту (кольца Рашига, Седла Берля, Инталокс и др.). Назначение слоя насадки - создание значительной поверхности контакта жидкой и газовой фаз в результате стекания жидкости по всей поверхности элементов насадки в виде пленки и прохождения газового потока в пустотах между элементами насадки и внутри них. Поверхность контакта фаз приблизительно равна суммарной поверхности насадки.

В тарельчатой колонне жидкая и газовая фазы контактируют только на тарелках, где газ барботирует через слой жидкости. Жидкость перетекает с верхней тарелки на нижнюю по вертикальным перетокам, а газовая фаза проходит снизу вверх через отверстия тарелок и всплывает в слоях жидкости в виде многочисленных пузырьков. Поверхностью контакта фаз является суммарная поверхность всех газовых пузырьков, в слоях жидкости на тарелках.

Подлежащая разделению бинарная смесь начального состава вводится на некоторую промежуточную по высоте колонны тарелку (или промежуточную точку по высоте насадочной колонны). Смесь подается при температуре ее кипения (или близкой к ней). В кубе-испарителе из кипящей в нем кубовой жидкости непрерывно образуется пар. Чтобы поддержать энергоемкий процесс парообразования, в куб необходимо подавать греющий водяной пар, при конденсации которого выделяется необходимая теплота. Образующиеся в кубе-испарителе пары движутся вверх, вступают в контакт с жидкой фазой, обогащаются летучим компонентом. При этом жидкость обедняется им. Пройдя весь путь пар поступает в дефлегматор, где конденсируется, делится на два потока (флегму и дистиллят). Флегма возвращается в колонну, чтобы паровому потоку было из чего извлекать летучий компонент, обедняется более летучим компонентом и приходит в куб-испаритель. Таким образом, в ректификационной колонне осуществляется непрерывный процесс разделения подаваемой в колонну исходной смеси на дистиллят и кубовый остаток. Основные достоинства насадочных колонн - способность работать при больших нагрузках по жидкости, на потоках жидкости и пара, содержащих механические примеси, на агрессивных потоках. Эти колоны просты по монтажу и изготовлению, долговечны.

1. Технологические расчеты 1.1 Расчет ректификационной колонны

Необходимо спроектировать ректификационную установку для непрерывного разделения исходной смеси. Тип насадки будет подбираться по ходу расчетов, однако основные из них будут керамические седла Берля и кольца Рашига.

 

1.1.1 Материальный баланс колонны

Для начала отметим, что легколетучим компонентом данной смеси является ацетон, а инертной фазой - метиловый спирт (метанол).

Зная производительность колонны по исходной смеси и необходимые концентрации (массовые), можно найти производительность колонны по дистилляту () и кубовому остатку () на основании уравнения материального баланса.

 (1)

 (2)

где  - массовые доли легколетучего компонента в исходной смеси, дистилляте и кубовом остатке соответственно, .

Отсюда, решая систему двух уравнений с двумя неизвестными

получим:

Нагрузка ректификационной колонны по пару и жидкости определяется рабочим флегмовым числом R и уравнениями рабочих линий в верхней и нижней частях колонны.

 (3)

где  - минимальное флегмовое число, вычисляемое по формуле

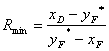 (4)

где - молярные доли легколетучего компонента в жидкости, ;  - концентрация легколетучего компонента в паре, находящегося в равновесии с жидкостью, . Для перехода от массовых долей легколетучего компонента к молярным используем соответствующие формулы:

 (5а),  (5б)

. (5в)

где М₁, М₂ - молярные массы легколетучего компонента и инертной фазы (M₁ = 58 кг/кмоль, M₂ = 32 кг/кмоль). Тогда получим:

 

.

По диаграмме y-x, интерполяционной формулой Лагранжа (приложение2), находим  при соответствующем значении :

.

Используя формулу (4) получим:

.

Далее по формуле (3):

.

Найдем уравнения рабочих линий:

а) для верхней (укрепляющей) части колонны:

 (6),  (6а)

б) для нижней (исчерпывающей) части колонны:

 (7)

где F - относительный молярный расход питания.

. Уравнение нижней части имеет вид:

. (7а)

1.1.2 Определение массовых и объёмных расходов пара и жидкости

Найдем средние массовые расходы жидкости , и пара , для верхней (индекс в) и нижней (индекс н) частей колонны по соответствующим формулам:

Для жидкости:

 (8)

 (8а)

где  - мольные массы дистиллята, кубового остатка и питания исходной смеси, определяемые по формулам (9а, б, в), кг/кмоль;  - средние мольные массы жидкостей в верхней и нижней частях колонны, определяемые по формулам (10а, б), кг/кмоль.

 (9а)

 (9б)

 (9в)

 (10а)

 (10б)

где  и  - средний молярный состав жидкостей в верхней и нижней частях колонны соответственно, определяемый по формулам:

.

Таким образом получим:

.

Подставляя полученные величины в уравнения (8) и (9) получим:

. Для пара:

 (11а) ,  (11б)

где  - средние мольные массы паров в верхней и нижней частях колонны, кг/кмоль, определяемые по формулам:

 (12а)

. (12б)

В данных формулах присутствуют средние молярные концентрации паров в верхней и нижней частях колонны, которые можно найти по уравнениям рабочих линий (6а) и (7а).

.

Тогда получим:

.

Подставляя полученные величины в уравнения (12) и (13) получим:

.

Для нахождения средних объёмных расходов жидкости и пара в верхней и нижней частях колонны необходимо найти их средние плотности.

Плотность жидкости определяем по формуле:

 (13а)

 (13б)

где  - массовые концентрации легколетучего компонента в верхней (индекс в) и нижней (индекс н) частях колонны,

; r₁ и r₂ - плотности ацетона и метилового спирта соответственно, кг/м³. Они зависят от температуры и подчиняются зависимостям:

 (14а)

 (14б)

Температуру жидкостей составов  и найдем используя диаграмму температура-состав (приложение1) и интерполяционную формулу Лагранжа.

 при

 при .

Тогда, используя формулы (14а, б), получим:

748.75 кг/м³

кг/м³

кг/м³

кг/м³.

Следует иметь в виду, что в формулах (13а, б) средняя концентрация легколетучего компонента в верхней и нижней частях колонны подставляется в массовых долях.

.

Далее по формулам (13а, б):

кг/м³

кг/м³.

Плотность пара определяем по формуле:

 (15а)

 (15б)

где Т₀ = 273 К;  - из формул (12а, б);  - средние температуры паров в верхней (индекс в) и нижней (индекс н) частях колонны, К.

Их определяем по диаграмме температура-состав (приложение 1), используя интерполяционную формулу Лагранжа.

 при

 при .

Тогда получим:

кг/м³

кг/м³.

Теперь определяем объемные расходы пара и жидкости:

Для жидкости:

.

Для пара

.

1.1.3 Гидравлический расчет колонны

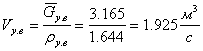
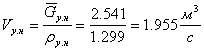Гидравлический расчет насадочных колонн включает в себя: определение рабочей скорости пара; определение диаметра колонны; расчет плотности орошения; расчет гидравлического сопротивления 1 м орошаемой насадки; определение активной поверхности насадки.

1.1.3.1 Определение рабочей скорости пара

В ректификационных колоннах при противотоке пара и жидкости необходимо знать так называемую рабочую скорость движения потоков пара, так как от этого зависит интенсивность процесса переноса целевого компонента между газовым потоком и пленкой жидкости. Чем больше скорость, тем интенсивнее процесс переноса, однако при больших скоростях сильно возрастает гидродинамическое сопротивление, что может привести к уносу жидкости из вертикального аппарата.

Для определения рабочей скорости сначала найдем предельную скорость пара w_пр, при которой произойдет захлёбывание колонны. Для её нахождения используем экспериментальную зависимость, обобщающую многие экспериментальные данные для процесса ректификации и абсорбции [1].

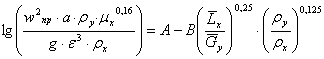 (16)

где  - предельная скорость пара в критических точках, м/с; а - удельная поверхность насадки, м²/м³; ε - свободный объём насадки, м³/м³; μ_х - динамический коэффициент вязкости жидкости, мПа∙с;  и  - массовые расходы жидкой и паровой (газовой) фаз, кг/с;  и  - плотность жидкости и пара соответственно, кг/м³; А и В - коэффициенты, значения которых можно найти в таблицах [1,2].

Динамический коэффициент вязкости жидкости в верхней и нижней частях колонны, в виду аддитивности данного свойства, найдем по формуле:

 (17а)

 (17б)

где  - средний мольный состав жидкостей в верхней и нижней частях колонны, ; m₁ и m₂ - динамические коэффициенты вязкости ацетона и метанола соответственно, . Они зависят от температуры и подчиняются зависимостям:

 (18а)

 (18б)

Температуры жидкостей были найдены ранее:

 при

 при . Тогда:

Согласно уравнениям (17а, б) получим:

Далее рассмотрим каждый интересующий нас тип насадки.

Седла Берля 12.5 мм: (a = 460 м²/м³; e = 0.68 м³/м³; A = 0.340; B = 1.75)

 

Верхняя часть:

.

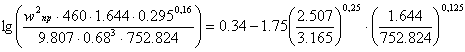
Нижняя часть:

 , .

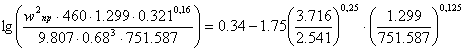
Седла Берля 25 мм: (a = 260 м²/м³; e = 0.69 м³/м³; A = 0.415; B = 1.75)

Верхняя часть:

.

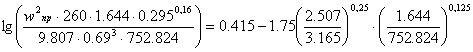
Нижняя часть:

.

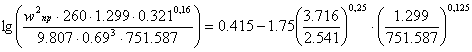
Седла Берля 38 мм: (a = 165 м²/м³; e = 0.7 м³/м³; A = 0.415; B = 1.75)

 

Верхняя часть:

.

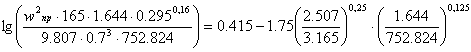
Нижняя часть:

.

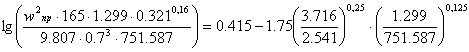
Керамические кольца Рашига 25*25*3: (a = 204 м²/м³; e = 0.74 м³/м³; A = - 0.125; B = 1.75)

 

Верхняя часть:

.

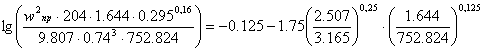
Нижняя часть:

.

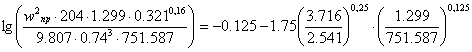
Керамические кольца Рашига 35*35*4: (a = 140 м²/м³; e = 0.78 м³/м³; A = - 0.125; B = 1.75)

 

Верхняя часть:

.

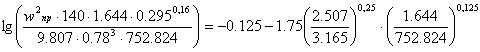
Нижняя часть:

.

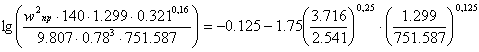
Стальные кольца Рашига 25*25*0.8: (a = 220 м²/м³; e = 0.92 м³/м³; A = - 0.125; B = 1.75)

 

Верхняя часть:

.

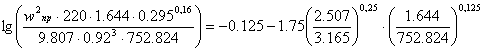
Нижняя часть:

.

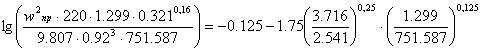
Стальные кольца Рашига 50*50*1: (a = 110 м²/м³; e = 0.95 м³/м³; A = - 0.125; B = 1.75)

 

Верхняя часть:

.

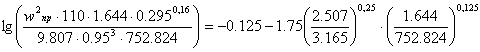
Нижняя часть:

.

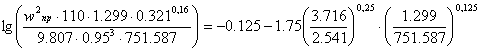
Рабочая скорость пара (газа) зависит от проводимого процесса, и рассчитывается по формуле:

 (19)

где k - коэффициент, зависящий от проводимого процесса и режима работы насадочной колонны.

Получим:

Седла Берля 12.5 мм: (k = 0.8)

 

Седла Берля 25 мм: (k = 0.7)

 

Седла Берля 38 мм: (k = 0.5)

 

Керамические кольца Рашига 25*25*3: (k = 0.8)

 

Керамические кольца Рашига 35*35*4: (k = 0.8)

 

Стальные кольца Рашига 25*25*0.8: (k = 0.8)

 

Стальные кольца Рашига 50*50*1: (k = 0.8)

 

1.1.3.2 Определение диаметра колонны и плотности орошения

Для определения диаметра колонны воспользуемся формулой:

 (20)

где V_y - объёмный расход пара при рабочих условиях в колонне, м³/с.

(Далее для верхней части колонны - индекс в, нижней - индекс н).

Седла Берля 12.5 мм:

 

Седла Берля 25 мм:

 

Седла Берля 38 мм:

 

Керамические кольца Рашига 25*25*3:

.

.

 

Керамические кольца Рашига 35*35*4:

.

.

Стальные кольца Рашига 25*25*0.8:

.

.

 

Стальные кольца Рашига 50*50*1:

.

.

Далее выберем по расчетной величине D стандартный аппарат и уточним рабочую скорость пара (газа) в верхней (в) и нижней (н) частях колонны. В нашем случае это 1.4 м или 1.6 м.

Рассмотрим оба варианта.

1.4 м:

1.6 м:

Уточнённую рабочую скорость газа проверяем по графической зависимости Эдулджи, где комплексы Y и X имеют следующий вид:

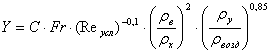 (21)

где  - критерий Фруда рассчитывается по номинальному размеру насадки d (м);  - критерий Рейнольдса (условный), также рассчитывается по номинальному размеру насадки d;  - динамический коэффициент вязкости жидкости, ;  и  - соответственно плотность воды при 20 ⁰С и орошаемой жидкости при температуре в колонне (см. формулы (14а, б)), кг/м³; и - плотность воздуха при 20 ⁰С и пара (газа) при температуре в колонне, кг/м³. (); С - коэффициент, зависящий от типа насадки.

Номинальный размер d для колец равен наружному диаметру, для седел Берля - соответствующий условный размер насадки.

 (22)

где  и  - объёмные расходы жидкости и пара (газа), м³/с; U - плотность орошения, м³/ (м²∙с).

Расчет плотности орошения производим по формуле:

 (23)

где V_x - объёмный расход жидкости, м³/с; S - площадь поперечного сечения колонны, м².

1.4 м: .

.

1.6 м: .

.

Сразу видим, что плотность орошения в колонне диаметром 1.6 м меньше, чем в 1.4 м, и даже не входит в рекомендуемый интервал (0.002-0.005) , следовательно далее будем рассчитывать колонну диаметром 1.4

Заранее определим:

Критерий Рейнольдса:

Седла Берля 12.5 мм:

 

 

Седла Берля 25 мм:

 

Седла Берля 38 мм:

 

Стальные кольца Рашига 25*25*0.8:

 

Стальные кольца Рашига 50*50*1:

 

Керамические кольца Рашига 25*25*3:

 

Керамические кольца Рашига 35*35*4:

Критерий Фруда:

Седла Берля 12.5 мм:

 

Седла Берля 25 мм:

 

Седла Берля 38 мм:

 

Стальные кольца Рашига 25*25*0.8:

 

Стальные кольца Рашига 50*50*1:

 

Керамические кольца Рашига 25*25*3:

 

Керамические кольца Рашига 35*35*4:

Далее воспользуемся формулой (22) и (21) для нахождения комплексов:

.

 

Седла Берля 12.5 мм: (С = 0.471)

.

Седла Берля 25 мм: (С = 0.471)

.

 

Седла Берля 38 мм: (С = 0.471)

.

 

Керамические кольца Рашига 25*25*3: (С = 1)

.

 

Керамические кольца Рашига 35*35*4: (С = 1)

.

 

Стальные кольца Рашига 25*25*0.8: (С = 1)

.

 

Стальные кольца Рашига 50*50*1: (С = 1)

.

Точки  на графической зависимости Эдулджи должны находиться ниже линии захлебывания, которая соответствует неустойчивому режиму работы колонны. Это означает, что насадки: Седла Берля 12.5 мм, Керамические кольца Рашига 25*25*3, 35*35*4, Стальные кольца Рашига 25*25*0.8 не удовлетворяют данным требованиям.

 

1.1.3.3 Гидравлическое сопротивление 1 м насадки

Одной из важных характеристик аппарата является гидравлическое сопротивление насадки. Хотя сопротивление колонны находят после определения общей высоты насадки, но на данном этапе проектирования необходимо убедиться в том, что рабочая скорость пара (газа), диаметр колонны и плотность орошения определены верно, то есть обеспечивают необходимый режим работы аппарата. Также это даст возможность выбрать наиболее подходящий тип насадки, из всех вышеперечисленных.

Сопротивление сухой насадки определим по формуле:

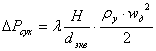 (24)

где Н = 1м - высота слоя насадки;  - скорость пара (газа) в свободном сечении насадки (действительная), м/с;  - эквивалентный диаметр насадки, м; l - коэффициент сопротивления, зависящий от режима движения пара (газа) и типа насадки.

Однако чаще всего используют графическую зависимость Эдулджи, по которой:

 

Седла Берля 25 мм:

.

 

Седла Берля 38 мм:

.

 

Стальные кольца Рашига 50*50*1:

.

Так как рекомендуемое гидравлическое сопротивление 400-800, то наиболее подходящими насадками являются седла Берля 38 мм. Однако заметим, что все насадки работают в наиболее благоприятной области работы ректификационной колонны, то есть в области подвисания.

 

1.1.3.4 Определение активной поверхности насадки

При нагрузках ректификационной насадочной колонны в большинстве случаев не вся поверхность насадки смочена жидкостью и не вся смоченная поверхность активна для процесса массопереноса. Доля активной поверхности насадки, участвующей в процессе массопереноса, определяется по соотношению:

 (25)

где U - плотность орошения, ; a - удельная поверхность насадки, м²/м³; p и q - постоянные, зависящие от типа и размера насадки. Далее индекс в - верхняя часть колонны, индекс н - нижняя.

В виду отсутствия данных по величине Y_а для седел, формула (25) применима только для колец Рашига.

Получим:

Стальные кольца Рашига

 

50*50*1: (p =; q = 0.012; a =110 м²/м³)

.

Для седел Берля воспользуемся другим методом вычисления, предварительно вычислив долю смоченной поверхности насадки Y по формуле:

 (26),

где ,  - критерий Рейнольдса для жидкости; A, b, p - константы; r_x и m_x - плотность и вязкость жидкости.

Тогда получим:

Седла Берля 25 мм: (A = 1; b = 0.089; p = 0.7; a = 260 м²/м³)

.

 

Седла Берля 38 мм:

 

(A = 1; b = 0.089; p = 0.7; a = 165 м²/м³)

.

Теперь найдем коэффициент , определяемый по графику зависимости k^’ от плотности орошения U:

Седла Берля 25 мм: .

Седла Берля 38 мм: .

В итоге найдем долю активной поверхности насадки Y_а:

Седла Берля 25 мм:

 

.

 

Седла Берля 38 мм:

.

При дальнейшем сравнении Y_а с минимально допустимыми значениями выяснилось, что все типы насадок удовлетворяют этому требованию.

Активная поверхность насадки находится как:

 (27)

 

Стальные кольца Рашига 50*50*1:

 

.

 

Седла Берля 25 мм:

 

.

 

Седла Берля 38 мм:

.

 

Окончательно выбираем насадку седла Берля 38мм, так как они удовлетворяют всем требованиям, работают в зоне подвисания, имеют меньшее гидравлическое сопротивление, обладают большей активной поверхностью.

1.1.4 Расчет высоты колонны

Расчет включает в себя:

расчет кинетических параметров: коэффициентов массоотдачи, высот единицы переноса;

определение высоты колонны;

расчет гидравлического сопротивления колонны.

Величину насадки Н определим через общее число единиц переноса n_oy и общую высоту единицы переноса по паровой фазе h_oy.

 (28)

Число единиц переноса:

Для нахождения числа единиц переноса необходимо вычислить интеграл:

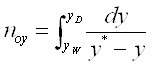 (29)

Величину интеграла определим численным методом, то есть разобьем равновесную кривую на отрезки, построим график зависимости  от y (x) (приложение 3), тогда значением интеграла будет площадь под этой кривой.

Составим таблицу:

Нижняя часть (7а):

x	y (x)	y*	y*-y (x)
0.011 0.05 0.1 0.15 0.191	0.011 0.07 0.146 0.221 0.284	0.02481 0.102 0.186 0.25839 0.31142	0.01381 0.032 0.04 0.03739 0.02742	72.41 31.25 25 26.745 36.47

Верхняя часть (6а):

x	y	y*	y*-y
0.191 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.688	0.284 0.291 0.332 0.372 0.413 0.454 0.494 0.535 0.576 0.616 0.657 0.688	0.31142 0.322 0.37819 0.428 0.47253 0.513 0.55051 0.586 0.62049 0.656 0.69728 0.73882	0.02742 0.031 0.04619 0.056 0.05953 0.059 0.05651 0.051 0.04449 0.04 0.04028 0.05082	36.47 32.258 21.65 17.857 16.8 16.95 17.7 19.608 22.477 25 24.526 19.677

Теперь находим общее число единиц переноса в верхней и нижней частях колонны:

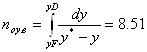
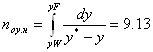
Высоты единиц переноса:

(Далее для верхней части колонны - индекс в, для нижней - индекс н).

Для расчета высот единиц переноса применяют формулы:

Для пара:

 (30)

где h_y - высота единицы переноса по паровой фазе, м;  - диффузионный критерий Прандтля для газа;  - массовая плотность орошения, кг/ (м²с); z - высота насадки одной секции (не должна превышать 3 м), м; ,  - динамический коэффициент вязкости жидкости, мПас; ; ,  - поверхностное натяжение воды при 20 ⁰С () и жидкости при средней температуре в колонне, Н/м; D - диаметр колонны, м;  - коэффициент, определяемый по экспериментальным данным; D_y - коэффициент диффузии для пара, который рассчитывается по формуле:

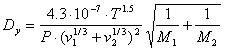 (31)

где T - средняя температура пара, К; P - среднее давление в колонне, атм;  - мольные массы легколетучего компонента и инертной фазы, кг/кмоль;  - мольные объемы растворенного вещества и растворителя, см³/моль. Они находятся по соответствующим таблицам.

ацетон:

метанол: .

Тогда получим:

.

Определим динамические коэффициенты вязкости паров по формулам:

 (32а)

 (32б)

где  - мольные массы: смеси паров (12а, б), ацетона и метанола соответственно, кг/кмоль; m₁, m₂ - вязкости паров чистых компонентов, . Их можно рассчитать по соответствующим зависимостям от температуры:

 (33а)

. (33б)

Тогда получим:

.

По формулам (32а, б):

.

Далее находим критерий Прандтля:

.

Определим по аддитивной формуле поверхностные натяжения жидкостей в верхней и нижней частях колонны:

 (34а)

 (34б)

где  - поверхностные натяжения ацетона и метанола, Н/м. Они зависят от температуры и подчиняются зависимостям:

 (35а)

 (35б)

Тогда:

.

По формулам (34а, б) находим:

.

Находим оставшиеся необходимые величины к формуле (30):

.

Тогда высота единиц переноса по паровой фазе равна: ()

.

 

Для жидкости:

 (36)

где h_x - высота единицы переноса по жидкой фазе, м;  - коэффициенты, определяемые графически по экспериментальным данным;  - диффузионный критерий Прандтля для жидкости. Коэффициент диффузии D_x для жидкости определяется по приближенной формуле:

 (37)

где D₂₀ - коэффициент диффузии бинарной смеси при t = 20⁰C, м²/с; t -температура смеси,⁰С;

b - температурный коэффициент, вычисляемый по формуле:

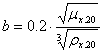 (38)

где  - динамический коэффициент вязкости, , и плотность смеси, , при температуре 20⁰С. Их можно найти используя формулы (20а, б) и (13а, б), а также зависимости от температуры (21а, б) и (14а, б):

кг/м³.

кг/м³.

кг/м³кг/м³.

 

Тогда по формуле (38):

.

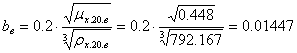
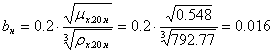Определим  по формуле:

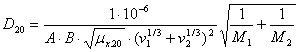 (39)

где А и В - коэффициенты, зависящие от свойств растворенного вещества и растворителя (A = 1, B = 2). Остальные обозначения находятся в формуле (31).

Тогда получим:

.

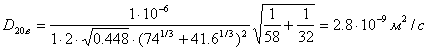
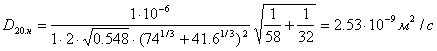Возвращаемся к формуле (37):

Тогда:

Высота единиц переноса для жидкой фазе: (Ф_в =0.037, Ф_н = 0.043, с = 0.67)

.

Далее определим общую высоту единицы переноса по формуле:

 (40)

где  - удельный расход жидкой фазы, кмоль/кмоль; m - тангенс угла наклона касательной к равновесной линии:  - в точке, соответствующей средним концентрациям для верхней и нижней частей колонны.

Получим:

.

.

Тогда высота насадки по формуле (29):

 , .

Общая высота насадки колонны:

,

Наконец общую высоту колонны найдем по формуле:

 (41)

где  - высота насадки одной секции, равна 3м;  - число секций ();  - высота промежутков между секциями, м;  и  - высота сепарационного пространства над насадкой и расстояние между днищем колонны и насадкой, соответственно, м.

В соответствии с рекомендациями [3]:

Диаметр колонны, м	, м	, м
1.2 - 2.2	1.0	2.0

Величина  зависит от размеров распределительных тарелок (ТСН-3) и при проектировании принимают  м. Примем h_р = 0.6 м.

Тогда общая высота колонны будет:

Расчет гидравлического сопротивления колонны:

Гидравлическое сопротивление насадки без учета сопротивления опорных решеток, распределительных тарелок можно рассчитать по уравнению

 (42). Тогда получим: .

1.1.5 Тепловой баланс ректификационной колонны

Тепловой баланс ректификационной колонны выражается общим уравнением:

 (43)

где Q_Д - расход теплоты, отнимаемый охлаждающим воздухом от конденсирующихся в дефлегматоре паров, Вт; Q_К - расход теплоты, получаемой кипящей жидкостью от конденсирующегося греющего пара в кубе-испарителе, Вт; и  - уход тепла с дистиллятом и кубовой жидкостью,  - ход тепла с исходной смесью, Вт;  - средние удельные теплоёмкости дистиллята, кубового остатка и исходной смеси, при соответствующих температурах, ; Q_потерь - тепловые потери колонны в окружающую среду, составляет 5% от полезно затрачиваемой работы, Вт;  - температуры кипения растворов, составов: дистиллята, кубового остатка и исходной смеси, ⁰С. Последние определяем по графической зависимости температура - состав (приложение 1):

 ⁰Спри

 ⁰Спри

 ⁰Спри .

Заранее определим удельные теплоемкости по аддитивной формуле:

 (44а)

 (44б)

 (44в)

где с₁ и с₂ - удельные теплоемкости легколетучего компонента и инертной фазы соответственно, . Они подчиняются зависимости от температуры:

 (45а)

 (45б)

Тогда получим:

дистиллят: 2.265

2.554

 

кубовый остаток:

исходная смесь: 2.279

2.567

 .

Расход теплоты, отдаваемой охлаждающему воздуху в дефлегматоре:

 (46)

где R - число флегмы; r_D - удельная теплота парообразования пара состава x_D в дефлегматоре, Дж/кг.

Для смеси паров она находится по правилу аддитивности:

 (47)

где  - удельные теплоты парообразования легколетучего компонента и инертной фазы при температуре дистиллята, Дж/кг. Они зависят от температуры и подчиняются зависимостям:

 (48а)

 (48б)

Тогда получим:

.

Возвращаясь к формуле (43) получим:

 

Потери составляют:

.

Тогда расход теплоты Q_Kравен:

.

1.2 Расчет теплообменных аппаратов, входящих в общую схему работы ректификационной колонны

 

1.2.1 Расчет теплообменного аппарата для подогрева исходной смеси водой

Известно, что температура теплоносителя (воды) в подогревателе исходной смеси, которая поступает при температуре 10 ⁰С, меняется от 98 до 70 ⁰С. Жидкости движутся противотоком.

Найдем конечную температуру смеси по диаграмме состав-температура (приложение 1), она равна: T_cmk = 60.38 ⁰С (при

).

t, 0С

 98

70

 60.38

10

F, м2

Найдем среднюю разность температур теплоносителей:

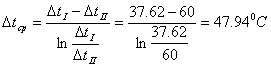
Тогда средние температуры греющей воды и смеси находятся как:

; .

Далее, зная среднюю температуру, найдем интересующие нас параметры теплоносителей при данной температуре:

Плотность: плотность смеси при данной температуре найдем по формуле (13) и зависимостям плотности компонентов данной смеси от температуры (14а, б):

 

ацетон:  кг/м³

метанол:  кг/м³

 кг/м³.

Плотность воды найдем из экспериментальных данных с помощью интерполяции:

 кг/м³.

Вязкость: динамический коэффициент вязкости определяем по аддитивной формуле (17) и зависимостям вязкости компонентов данной смеси от температуры (18а, б):

ацетон:

метанол:

.

Вязкость воды найдем из экспериментальных данных с помощью интерполяции:

.

Теплоемкость:

Теплоемкость смеси найдем по аддитивной формуле:

 (49)

где с₁ и с₂ - теплоемкости легколетучего компонента и инертной фазы соответственно, , которые зависят от температуры и подчиняются зависимостям:

 (50а)

 (50б)

Тогда получим:

.

Теплоемкость воды найдем из экспериментальных данных с помощью интерполяции:

.

Теплопроводность: теплопроводность найдем по аддитивной формуле:

 (51)

где l₁ и l₂ - теплопроводности легколетучего компонента и инертной фазы соответственно, , которые зависят от температуры и подчиняются зависимостям:

 (52а)

 (52б)

Тогда получим:

.

Теплопроводность воды также найдем из экспериментальных данных с помощью интерполяции:

.

Теперь запишем уравнение теплового баланса для теплообменника:

 (53)

Из него найдем массовый расход греющей воды:

 , , .

Для того, чтобы рассчитать величину теплообменной поверхности, необходимо найти коэффициент теплопередачи:

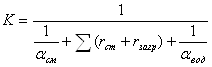 (54)

где  - термические сопротивления стенки и загрязнений соответственно, ; по справочнику

) -

 - коэффициенты теплоотдачи теплоносителей (от стенки к смеси и от воды к стенке соответственно,

, находятся по формуле:

 (55)

где Nu - критерий Нуссельта, зависит от вида передачи тепла между теплоносителями;

d - характерный размер системы (d_вн или d_нар), м;

l - коэффициент теплопроводности теплоносителей, .

Следует отметить, что нахождение коэффициентов теплоотдачи является главной задачей расчета теплообменного аппарата.

Для начала зададим ориентировочное значение K_ор (по справочнику [1]), и найдем ориентировочное значение теплообменной поверхности (K_ор = 300 ):

Получим:

.

Из данной величины следует, что проектируемый теплообменник может быть любым, кроме теплообменника “труба в трубе", так как существуют большие термические напряжения, связанные с большой разностью температур теплоносителей.

Для интенсивного теплообмена попробуем подобрать аппарат с турбулентным режимом течения теплоносителей. Смесь направим в трубное, а воду - в межтрубное пространство.

А) В теплообменных трубах 20*2 мм теплообменников скорость течения смеси при  должна быть более:

.

Проходное сечение трубного пространства при этом должно быть менее:

.

В) В теплообменных трубах 25*2 мм теплообменников скорость течения смеси при  должна быть более:

.

Проходное сечение трубного пространства при этом должно быть менее:

.

Под эти условия подходят одноходовые теплообменники: 20*2 - 159 мм, 25*2 - 159 мм. Однако, учитывая, что поверхность теплообмена одного такого теплообменника мала, то придется использовать несколько последовательно соединенных, что является их существенным недостатком. Поэтому не исключаем применение многоходовых теплообменников и большего диаметра, но одного.

Рассмотрим намеченные теплообменники:

Вариант 1: Кожухотрубчатый теплообменник диаметром 159 мм с трубами 20*2 мм (ГОСТ 15120-79):

Скорости и критерии Рейнольдса теплоносителей:

Смесь:

 

 (56)

где  - проходное сечение трубного пространства; n - число труб; d_вн - внутренний диаметр трубы, м.

Получим:

.

Вода:  (57)

где  - проходное сечение межтрубного пространства. Здесь .

Получим:

где d_нар - наружный диаметр труб, определяющий линейный размер при поперечном обтекании, м.

Тогда теплоотдача для обоих потоков описывается уравнениями:

Смесь: при развитом турбулентном течении в трубах

 

 (58)

Вода: при поперечном омывании потоком трубного пучка

 

 (59)

где e_l= 1; e_j = 0.6 - коэффициент, учитывающий угол атаки теплоносителя в межтрубном пространстве; Pr - критерий Прандтля при средней температуре жидкости, Pr_w - то же, но при температуре стенки со стороны теплоносителя. Оба находятся по общей формуле:

 (60)

Найдем критерии Прандтля при средней температуре для жидкостей:

Ввиду того, что температуры стенок со стороны теплоносителей неизвестны, воспользуемся методом итераций (приближений). Он сводится к следующему:

Зная средние интегральные температуры теплоносителей  зададим температуру стенки со стороны горячего (воды) теплоносителя в интервале . Например .

Находим теплофизические свойства воды при данной температуре, используя экспериментальные данные:

.

Тогда по формуле (60):

.

Зная критериальные уравнения (59) и формулу (55) найдем критерий Нуссельта, а затем и коэффициент теплоотдачи от горячей воды к стенке:

.

Найдем тепловой поток:

.

Так как входящий тепловой поток  должен быть равен потоку, проходящему поперек стенки, и соответственно выходящему, то мы можем найти температуру стенки со стороны холодного теплоносителя (смеси):

 (61)

.

Определяем теплофизические свойства смеси при данной температуре по формулам (17), (49), (51) и зависимостям (18а, б), (50а, б), (52а, б):

.

Тогда:

.

Зная критериальное уравнение движения (58), найдем критерий Нуссельта и коэффициент теплоотдачи от стенки к смеси:

.

Вычислим тепловой поток:

.

При стационарном процессе теплопередачи значения тепловых потоков должны быть одинаковыми. Если это не так, то необходимо заново задать температуру стенки со стороны горячего теплоносителя, до тех пор пока тепловые потоки не будут равны.

Можно заметить, что для этого необходимо повысить , например до . Тогда (без подробных расчетов):

.

.

. .

(61) Þ.

Определяем теплофизические свойства смеси:

.

Тогда:

.

 .

Теперь необходимо слегка понизить температуру , например до . Тогда получим:

,

 .

Теперь определим коэффициент теплопередачи:

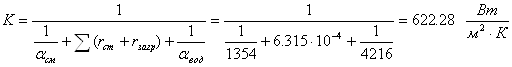
Определим расчетную площадь поверхности теплопередачи:

С запасом 10% .

А) Принимаем к установке аппараты длиной 2 м. Площадь поверхности теплообмена одного аппарата равна 2.5 м². Необходимое число аппаратов:

Примем N = 4. Запас поверхности составляет при этом:

%.

Масса одного аппарата диаметром 159 мм с трубами длиной 2 м равна M₁ = 217кг, масса элементного теплообменника из N аппаратов:

.

Б) Принимаем к установке аппараты длиной 3 м. Площадь поверхности теплообмена одного аппарата равна 3.5 м². Необходимое число аппаратов:

Примем N = 3. Запас поверхности составляет при этом:

%.

Масса одного аппарата диаметром 159 мм с трубами длиной 3 м равна M₁ = 263кг, масса элементного теплообменника из N аппаратов:

.

Вариант 2: Кожухотрубчатый теплообменник диаметром 159 мм с трубами 25*2 мм (ГОСТ 15120-79):

Расчеты проводим по иной схеме.

Скорости и критерии Рейнольдса теплоносителей:

 

.

 

Теплоотдача подчиняется тем же уравнениям, что и ранее, (58) и (59).

Критерии Прандтля при средней температуре для жидкостей те же самые, что и раньше:  и

Теперь примем сомножитель  равным единице для обоих потоков, что допускается в нашем случае.

Тогда коэффициенты теплоотдачи от воды к стенке и от стенки к смеси найдем из формул (58), (59) и (55):

Смесь:

.

Вода:

.

Коэффициент теплопередачи:

.

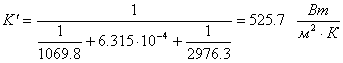Ввиду того, что тепловой поток постоянен, найдем:

где сумма равна

Проверим:

.

Отсюда температуры стенок:

.

Введем поправку в коэффициент теплоотдачи, определив :

Смесь:

По формуле (60) определим , учитывая, что вязкость, теплоемкость и теплопроводность берутся при температуре стенки .

Их можно найти по формулам: (17, 18а, б), (49,50а, б) и (51,52а, б):

.

 

Вода:

Найдем  по формуле (60), а входящие в него параметры, для воды при температуре стенки , найдем из экспериментальных данных с помощью интерполяции:

.

Коэффициенты теплоотдачи равны:

.

Исправленные значения:

.

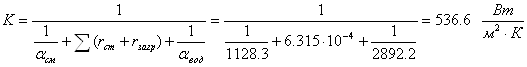
Дальнейшее уточнение коэффициентов теплоотдачи и других величин не требуется, так как расхождение между ними не превышает 2%.

Теперь определим расчетную площадь поверхности теплопередачи:

 С запасом 10% .

А) Принимаем к установке аппараты длиной 2 м. Площадь поверхности теплообмена одного аппарата равна 2 м². Необходимое число аппаратов:

Примем N = 5. Запас поверхности составляет при этом:

%.

Масса одного аппарата диаметром 159 мм с трубами длиной 2 м равна M₁ = 211кг, масса элементного теплообменника из N аппаратов:

.

Б) Принимаем к установке аппараты длиной 3 м. Площадь поверхности теплообмена одного аппарата равна 3 м².

Необходимое число аппаратов:

Примем N = 4. Запас поверхности составляет при этом:

%.

Масса одного аппарата диаметром 159 мм с трубами длиной 3 м равна M₁ = 255кг, масса элементного теплообменника из N аппаратов: .

Вариант 3: Кожухотрубчатый теплообменник диаметром 325 мм с трубами 25*2 мм двухходовой (ГОСТ 15120-79):

Число труб одного хода n1 = 28 шт, общее - n = 56 шт. Сечение одного хода трубного пространства .

Так как теплообменник двухходовой то необходимо заново вычислить среднюю разность температур, для смешанного тока., пользуясь соотношениями:

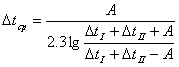 (62)

где ;  - изменение температуры горячего теплоносителя;  - изменение температуры холодного теплоносителя.

Тогда:

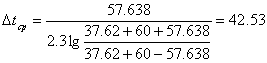 ⁰C

Тогда средняя температура смеси равна:

.

Далее, зная среднюю температуру смеси, найдем ее параметры при данной температуре:

Плотность:

По формуле (13) и зависимостям плотности компонентов данной смеси от температуры (14а, б) вычислим:

ацетон:  кг/м³

метанол:  кг/м³

 кг/м³.

Вязкость:

Динамический коэффициент вязкости определяем по аддитивной формуле (17) и зависимостям вязкости компонентов смеси от температуры (18а, б):

ацетон:

метанол:

.

Теплоемкость:

Теплоемкость смеси найдем по аддитивной формуле (49) и зависимостям (50а, б):

.

Теплопроводность:

Теплопроводность найдем по аддитивной формуле (51) и зависимостям (52а, б):

.

Теперь рассчитываем теплообменный аппарат таким же образом, что и раньше:

Из уравнения теплового баланса (53) найдем массовый расход греющей воды:

, .

Скорости и критерии Рейнольдса теплоносителей:

Теплоотдача для обоих потоков описывается теми же уравнениями:

Смесь: при развитом турбулентном течении в трубах

 

Вода: при поперечном омывании потоком трубного пучка

 

где e_l= 1; e_j = 0.6 - коэффициент, учитывающий угол атаки теплоносителя в межтрубном пространстве; Pr - критерий Прандтля при средней температуре жидкости, Pr_w - то же, но при температуре стенки со стороны теплоносителя. Найдем критерии Прандтля при средней температуре для жидкостей:

,

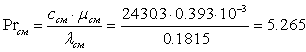Также примем сомножитель  равным единице для обоих потоков.

Тогда коэффициенты теплоотдачи от воды к стенке и от стенки к смеси найдем из формул (58,59) и (55):

Смесь:

. Вода:

,

Тогда коэффициент теплопередачи:

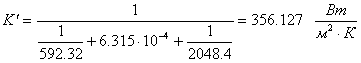
Далее найдем значения температур стенок со стороны каждого теплоносителя, исходя из того, что поверхностная плотность теплового потока одинакова на всем пути передачи теплоты:

Найдем:

,

.

Проверим:

.

Отсюда температуры стенок:

.

Введем поправку в коэффициент теплоотдачи, определив :

Смесь:

По формуле (60) определим , учитывая, что вязкость, теплоемкость и теплопроводность берутся при температуре стенки . Их можно найти по формулам: (17, 18а, б), (49,50а, б) и (51,52а, б):

.

 

Вода:

Найдем  по формуле (60), а входящие в него параметры, для воды при температуре стенки , найдем из экспериментальных данных с помощью интерполяции:

Коэффициенты теплоотдачи равны:

Исправленные значения:

.

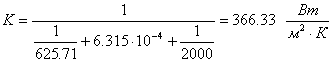
Дальнейшее уточнение коэффициентов теплоотдачи и других величин не требуется, так как расхождение между ними не превышает 2%.

Теперь определим расчетную площадь поверхности теплопередачи:

 С запасом 10% .

А) Принимаем к установке аппараты длиной 3 м. Площадь поверхности теплообмена одного аппарата равна 13 м². Необходимое число аппаратов:

Примем N = 2. Запас поверхности составляет при этом:

%.

Масса одного аппарата диаметром 325 мм с трубами длиной 3 м равна M₁ = 645кг, масса элементного теплообменника из N аппаратов:

.

Б) Принимаем к установке аппараты длиной 4 м. Площадь поверхности теплообмена одного аппарата равна 17.5 м².

Необходимое число аппаратов:

Примем N = 1. Запас поверхности составляет при этом:

%.

Масса одного аппарата диаметром 325 мм с трубами длиной 4 м равна M₁ = 780кг.

 

1.2.2 Расчет конденсатора-дефлегматора

В данной установке конденсат охлаждают воздухом с начальной температурой 10 ⁰С. Количество теплоты, которое отдает конденсирующийся пар, было рассчитано в главе 1.1.5 и составляет . Допускаем, что полученный конденсат не охлаждается в конденсаторе.

Для начала зададим конечную температуру воздуха, например

 0C.

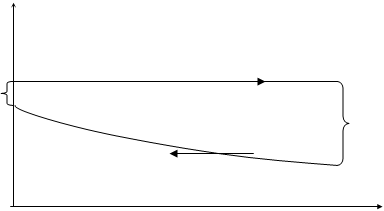
ё t, 0С

дистиллят

 55.361

50

воздух 10

F, м2

Вычислим среднюю разность температур по формуле (62) для перекрестного хода:

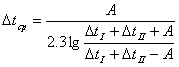, где .

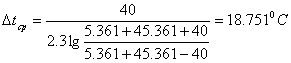
Тогда средняя температура воздуха:

Теплоемкость и плотность воздуха найдем из справочных данных:

, .

Далее, пользуясь уравнением теплового баланса, найдем массовый расход воздуха:

,

Объемный расход воздуха:

.

Так как подробный расчет не требуется, то по справочным данным принимаем коэффициент теплопередачи , и находим расчетное значение теплообменной поверхности по формуле:

.

С запасом 10% это будет: .

Выбираем конденсатор диаметром 1400 мм с трубами 20*2мм длиной 6м, двухходовой. Тогда необходимое количество аппаратов находится как:

Берем N = 4, тогда запас поверхности равен:

%

1.2.3 Расчет куба-испарителя.

В кубе - испарителе происходит кипение смеси состава и соответствующее его испарение. Подогрев происходит горячей водой. Количество теплоты, необходимое для процесса кипения и испарения было найдено в главе 1.1.5, и составляет Q_K = 2.38 МВт.

Зная температуру кубового остатка  и греющей воды найдем среднюю разность температур при противотоке:

.

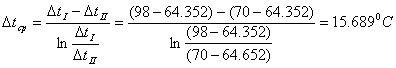Тогда средняя температура греющей воды:

.

Теплоемкость воды при данной температуре определим по справочным данным:

.

Используя уравнение теплового баланса найдем массовый расход греющей воды:

, .

Так как подробный расчет не требуется, то по справочным данным принимаем коэффициент теплопередачи , и находим расчетное значение теплообменной поверхности по формуле:

.

С запасом 10% это будет: .

Выбираем испаритель диаметром 1000 мм с трубами 25*2 мм длиной 3м:

Запас поверхности равен:

%.

1.2.4 Расчет холодильников для охлаждения продуктов ректификации

Охлаждение дистиллята:

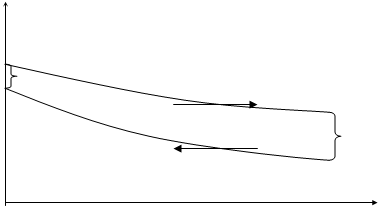
Дистиллят выходит из конденсатора при температуре , и его охлаждают воздухом с начальной температурой 10⁰С до 30⁰С.

Примем конечную температуру воздуха также 50⁰С.

t, 0С

 55.361

  Дистиллят

50 30

воздух

10

F, м2

Найдем среднюю разность температур при противотоке:

.

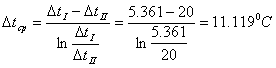Тогда средняя температура воздуха и дистиллята:

.

Теплоемкость воздуха и дистиллята при данных температурах:

.

Далее используя уравнение теплового баланса найдем расход воздуха:

.

Плотность воздуха при данной температуре:

Объемный расход воздуха:

Так как подробный расчет не требуется, то по справочным данным принимаем коэффициент теплопередачи , и находим расчетное значение теплообменной поверхности по формуле:

.

С запасом 10% это будет: .

Выбираем теплообменник диаметром 600 мм с трубами 20*2 мм длиной 4м, так как холодильники данного типа не изготавливают:

Запас поверхности равен:

%.

Охлаждение кубового остатка:

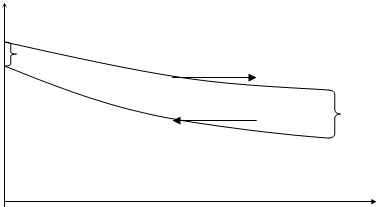
Кубовый остаток выходит из испарителя при температуре  и его охлаждают воздухом, с начальной температурой 10⁰С, до 30⁰С.

Примем конечную температуру воздуха также 50⁰С.

t, 0С

 64.352

 

кубовый остаток

50 30

воздух

10

F, м2

Найдем среднюю разность температур при противотоке:

.

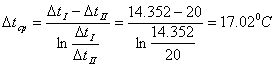Тогда средняя температура воздуха и дистиллята:

.

Теплоемкость воздуха и дистиллята при данных температурах:

.

Далее используя уравнение теплового баланса найдем расход воздуха:

.

Плотность воздуха при данной температуре:

Объемный расход воздуха:

Так как подробный расчет не требуется, то по справочным данным принимаем коэффициент теплопередачи , и находим расчетное значение теплообменной поверхности по формуле:

. С запасом 10% это будет: .

Выбираем теплообменник диаметром 1000 мм с трубами 25*2 мм длиной 3м. Запас поверхности равен:

%.

Следует отметить, что в двух последних холодильниках смеси, текущие в трубном пространстве, имеют очень маленькую скорость, зато охлаждающий воздух имеют очень даже невысокую скорость, и также необходимо всего один аппарат.

Вывод

В данном курсовом проекте рассмотрены основные узлы ректификационной установки для непрерывного разделения смеси ацетон-метиловый спирт. Установка имеет производительность: по исходной смеси 6.6 т/ч, по дистилляту 2.37 т/ч, по кубовому остатку 4.23 т/ч.

В состав установки входят: