Навигация
5. Результат
6.
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200+e1 |
| 0 | e2+e1 | 200-e2 | ||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 200 | 300-e2 | 100+e2 | ||||
| A3 | 23 | 40 | 10 | 12 | 21 | 200+e2 |
| 200 | e2 | |||||
| bi | 200 | 300+e1 | 200 | 100+e2 | 200 | 600+e1+e2 |
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200 |
| 0 | 200 | |||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 200 | 300 | 100 | ||||
| A3 | 23 | 40 | 10 | 12 | 21 | 200 |
| 200 | ||||||
| bi | 200 | 300 | 200 | 100 | 200 | 600 |
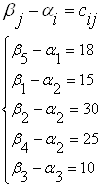
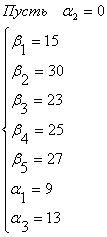
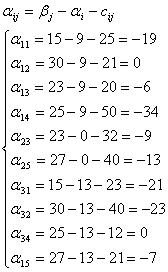
Так в системе 
нет положительных чисел, то найденный план называется оптимальным.
Ответ: F=19100
Задача 4
| № | b1 | b2 | c11 | c12 | c22 | extr | a11 | a12 | a21 | a22 | p1 | p2 | Знаки огр. | |
| 1 | 2 | |||||||||||||
| 8 | 1 | 2 | –1 | 0 | –1 | max | 1 | 2 | 1 | 1 | 16 | 8 | £ | = |
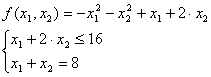
Приведем систему к стандартному виду:
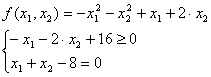
Определение стационарной точки:
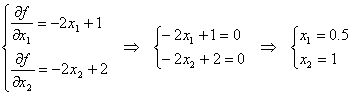
Очевидно, что данные координаты не удовлетворяют условиям ограничений.
1. Проверка стационарной точки на относительный max или min:
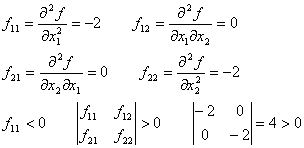
Стационарная точка является точкой относительного максимума.
2. Составление функции Лагранжа:
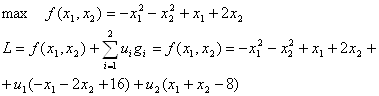
3. Применим теорему Куна-Таккера:
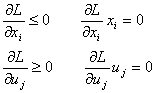
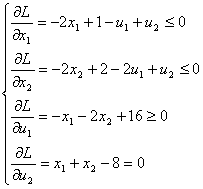
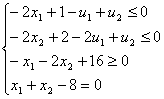
Нахождение решения системы:
Перепишем эту систему, оставив все переменные в левой части:
Из уравнения 3 системы следует, что x1=8-x2:
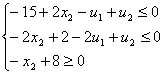
Тогда:
Для обращения неравенств системы в равенства введём V1, V2, W и преобразуем систему:
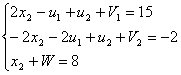
Запишем условия дополняющей нежесткости:
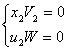
4. Метод искусственных переменных:
Введем искусственные переменные 
,
в первое и второе уравнения со знаками, совпадающими со знаками соответствующих свободных членов:
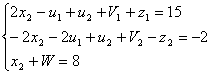
Далее решаем полученную задачу линейного программирования, для этого из 1 и 2 уравнений выражаем переменные , и принимаем их в качестве базисных.
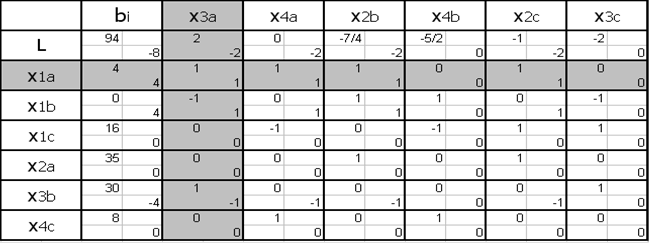
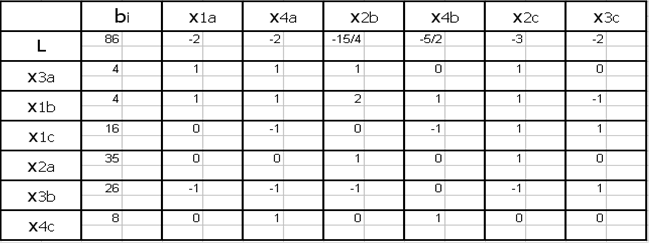
Составляем симплекс-таблицу:
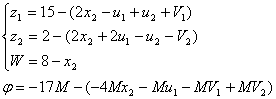
| bi | x2 | u1 | u2 | V1 | V2 | |||||||
| -17M | -4M | -M | 0 | -M | M | |||||||
| M | M | 0.5M | -0.5M | 0 | -0.5M | |||||||
| z1 | 15 | 2 | -1 | 1 | 1 | 0 | ||||||
| 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | |||||||
| z2 | 2 | 2 | 2 | -1 | 0 | -1 | ||||||
| 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | |||||||
| W | 8 | -1 | 0 | 0 | 0 | 0 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| bi | x2 | z2 | u2 | V1 | V2 | |||||||
| -16M | -3M | 0.5M | -0.5M | -M | 0.5M | |||||||
| 3M | 3M | 1.5M | -1.5M | 0 | -1.5M | |||||||
| z1 | 16 | 3 | 0.5 | 0.5 | 1 | -0.5 | ||||||
| -3 | -3 | -1.5 | 1.5 | 0 | 1.5 | |||||||
| u1 | 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
| 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | |||||||
| W | 8 | -1 | 0 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | |||||||
| bi | u1 | z2 | u2 | V1 | V2 | |||||||
| -13M | 3M | 2M | -2M | -M | -M | |||||||
| 13M | -3M | M | 2M | M | M | |||||||
| z1 | 13 | -3 | 1 | 2 | 1 | 1 | ||||||
| 13 | -3 | 1 | 2 | 1 | 1 | |||||||
| x2 | 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| W | 9 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| bi | u1 | z2 | u2 | z1 | V2 | |||||||
| 0 | 0 | 3M | 0 | M | 0 | |||||||
| V1 | 13 | -3 | 1 | 2 | 1 | 1 | ||||||
| x2 | 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
| W | 9 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
u1=u2=z1=z2=V2=0
V1=13
x2=1
W=9
x1=8-x2=7
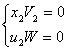
Ответ: x2=1, x1 =7, 
Список используемой литературы
1. Волков И. К., Загоруйко Е. А. Исследование операций. – Москва: Издательство МГТУ имени Баумана Н. Э., 2000г. – 436с.
2. Плотникова Н.В. «Исследование операций» Часть 1. Линейное программирование.
3. Плотникова Н.В. «Лекции по курсу теория систем»
Похожие работы
... точки на относительный максимум или минимум , , следовательно, стационарная точка является точкой относительного максимума. 3) Составление функции Лагранжа Применяем к функции Лагранжа теорему Куна-Таккера. I II 4) Нахождение решение системы I. Оставим все свободные переменные в правой части. (1) (из II) Система уравнений II определяется условиями ...
... называют системообразующие, системоохраняющие факторы, важными среди которых являются неоднородность и противоречивость ее элементов. Коммуникативность. Эта закономерность составляет основу определения системы, предложенного В. Н. Садовским и Э. Г, Юдиным в книге «Исследования по общей теории систем». Система образует особое единство со средой; как правило, любая исследуемая система представляет ...
... буржуа. М. 1987. Гвардини Р. Конец Нового времени//"Вопросы философии", 1990. Легенда о докторе Фаусте. М. 1978. I. АНТРОПОЛОГИЧЕСКАЯ ТРАДИЦИЯ В КУЛЬТУРОЛОГИИ 1. КУЛЬТУРОЛОГИЯ - ИНТЕГРАЦИЯ ЗНАНИЙ О КУЛЬТУРЕ Антропологическая традиция в культурологии — традиция исследования культуры в культурной и социальной антропологии. Культурология как интегративная наука формируется на стыке целого ряда ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
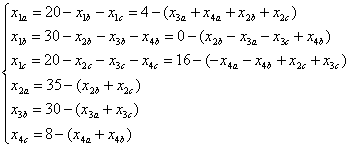
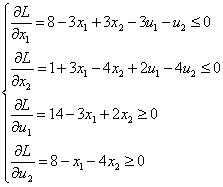
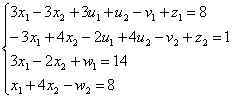
0 комментариев