Навигация
ОСНОВНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ТАБЛИЦ СМЕРТНОСТИ
3. ОСНОВНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ТАБЛИЦ СМЕРТНОСТИ
3.1 Построение полной таблицы смертности
Построение таблиц смертности является в принципе несложной, но достаточно трудоемкой вычислительной процедурой. Она включает в себя несколько этапов:
расчет значений исходного показателя для всех возрастов на основе данных статистики смертности (распределения умерших по возрастам);
если необходимо, обработку этого ряда значений для уст ранения искажений, вызванных возрастной аккумуляцией;
интерполяцию ряда значений для устранения возможных пропусков или экстраполяцию для расчета значений для самых старших возрастов;
вычисление остальных функций таблицы смертности.
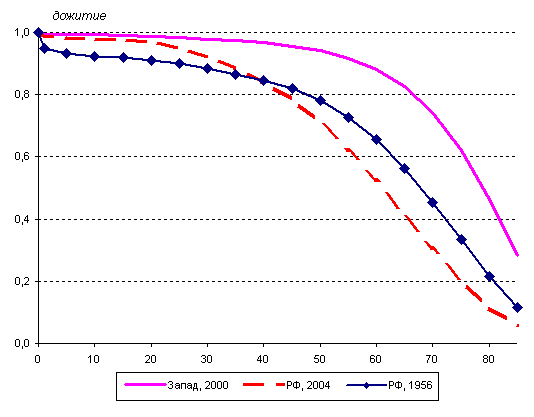
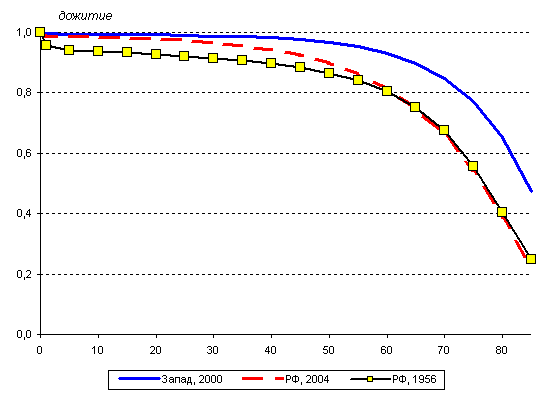
Основная методическая проблема построения таблиц смертности, как уже говорилось, связана с переходом от реальных показателей повозрастной смертности к табличным вероятностям умереть в данном возрасте, т.е. от тх* к qx.
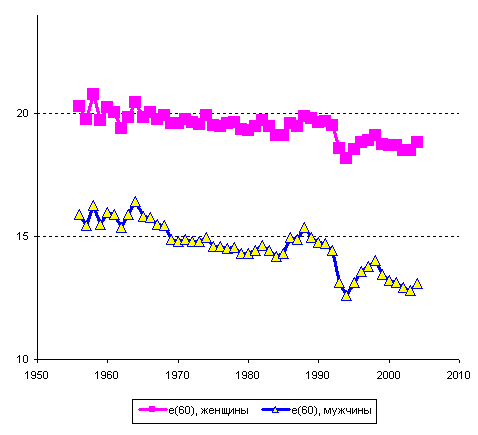
Методы построения таблиц смертности занимают большое место в демографии. Можно повторить уже сказанное выше, что история демографии в значительной мере совпадает с историей разработки и совершенствования этих методов.
Современные таблицы смертности рассчитываются с помощью т.н. косвенного, или демографического, метода. Демографический метод назван так потому, что в его основе лежат данные о повозрастной смертности, а также о возрастно-половой структуре населения, получаемые во время переписей и текущего учета. Косвенным этот метод назван, чтобы противопоставить его т.н. прямому методу, или, иначе, методу Р. Бека, основанному на непосредственном расчете показателей таблицы смертности в ситуации, когда известно распределение смертей на элементарные совокупности сетки Лексиса.
Исходным показателем здесь служит повозрастной коэффициент смертности, который приравнивается к табличному коэффициенту смертности (dx/Lx) и на основе которого определяются все функции таблицы смертности, начиная, разумеется, с вероятности умереть в возрасте х лет. Демографический метод позволяет строить таблицы смертности, наиболее адекватно отражающие ее уровень. При этом на величину итоговых показателей не влияют колебания чисел родившихся и умерших в годы, предшествовавшие расчету.
Проблема, связанная с переходом от повозрастных коэффициентов смертности к вероятностям смерти на возрастном интервале (х, х+п) лет, состоит в том, что первые, как известно, рассчитываются по отношению к общему числу человеко-лет, прожитых населением на этом возрастном интервале, или к его приближению, т.е. среднегодовому населению. Вторые же рассчитываются по отношению к численности населения в начале возрастного интервала. Чтобы построить таблицу смертности, надо установить соотношение между ними, т.е. между тх и qx. Иначе говоря, нужно перейти от тхк qx6.
Пусть Nx- число доживающих до возраста х лет в реальном населении. Из этого числа до следующего возраста х+1 лет не доживет Dx.
Вместе с тем повозрастной коэффициент смертности тхравен отношению Dx к числу человеко-лет, прожитых Nx в течение интервала (х, х + 1). Это число человеко-лет, в свою очередь, равно сумме двух слагаемых:
Первое слагаемое - это (Nx - Dx, т.е. число человеко-лет, прожитых на этом интервале возраста теми, кто дожил до возраста (х, х + 1).
Второе слагаемое - это число человеко-лет, прожитых на этом интервале возраста теми, кто не дожил до возраста (х, х + 1), т.е. умер на этом интервале возраста. Это число равно a'x-Dx.
Последнее выражение есть знакомая формула расчета повозрастного коэффициента смертности.
Решим уравнение
Рх = (NX -Dx) + a'x Dx
относительно Nx:
Nx=Px+(1-a'xDx)
Подставим это выражение в приведенную выше формулу для qx.
Если числитель и знаменатель этого выражения разделить на Рx, то получим искомое базисное соотношение между qx и тх:
Величины а0 а1...варьируют от страны к стране в зависимости от уровня смертности. Для развивающихся стран, в которых смертность высока, обычно принимается а0 - 0,3, a1 - 0,4 и 0,5 для всех остальных. Там же, где смертность низка, наилучшей величиной для а0 является 0,1. В целом выбранная величина не является критичной, за исключением а0. Более того, существует альтернативный путь определения q0 без использования вышеприведенной формулы. Речь идет о простом приравнивании q0 к коэффициенту младенческой смертности. Newell С. Methods and Models in Demography. London. 1988. P. 69.
Приведенное выше уравнение является фундаментальным для построения современных таблиц смертности. Зная все qx и выбрав корень таблицы смертностиl0, можно, используя приведенные выше соотношения между ними, построить все остальные функции таблиц смертности.
3.2 Построение краткой таблицы смертности
Идея и метод построения краткой таблицы смертности аналогичны только что рассмотренным для полных таблиц смертности. Разница только в длине возрастного интервала. Длина типичного -того интервала возраста (хi,xi+l) в кратких таблицах равна ni = xi+1- xi, т.е. превышает 1 год. Чаще всего она равна 5 годам. Существенным элементом здесь является средняя доля этого интервала, прожитая теми, кто умер в этом возрастном интервале.
Эта доля, обозначаемая аi,является обобщением рассмотренной выше доли а'х последнего года жизни. Определение этой доли является отдельной задачей, которая может решаться по-разному. Одно из возможных решений приведено во вставке на этой странице. В целом, к счастью, за исключением самых молодых возрастов, выбор величины ai не является критичным для построения кратких таблиц смертности. Обычно конвенционально принимается, что a0 = 0,1 для стран с низкой смертностью и 0,3 - для стран с высокой смертностью. Все прочие значения этого параметра принимаются равными 0,4 для всех остальных возрастных интервалов7.
Вместе с тем, как показал Чин Лонг Чань8, величина ai не зависит от конкретных значений коэффициента смертности в год, для которого рассчитывается краткая таблица смертности, а определяется лишь тенденцией изменения вероятности смерти внутри возрастного интервала (хi, xi+l) и может быть рассчитана на основании данных об одногодичных вероятностях смерти. Наличие специальных компьютерных программ построения таблиц смертности делает расчет этого параметра тривиальной задачей.
Задача построения всех функций таблицы смертности по возрастным коэффициентам смертности jn (x), которые считаются равными табличным, на практике очень важна. Для ее решения надо решить специальное уравнение 1(х+п) - 1(х) - = -nm(х)nLp которое называется основным уравнением таблицы смертности. Существуют различные методы решения этого уравнения. Я укажу простейший.
Формула для вероятности умереть на возрастном интервале (xj, xi+1) лет аналогична формуле для полных таблиц смертности.
Эта формула построена при предположении, что внутри возрастного интервала (х + п) вероятность смерти или постоянна, или меняется линейно (в возрастных интервалах 0-1 год и 1- 4 года). Если же гипотеза линейности не принимается, то используют альтернативную формулу Гомперца (1825) и Фарра (1864), в которой гипотеза линейности заменяется гипотезой экспоненциального изменения вероятности смерти на возрастном интервале (х + п) лет. Соответственно, nqx = 1 - nрх.
Для возрастного интервала 0 - 1 год как альтернатива иногда просто приравнивают q0к коэффициенту младенческой смертности.
Все прочие функции краткой таблицы смертности рассчитываются исходя из вычисленных ai,qiи корня таблицыl0.
Числа умирающих (di) на возрастном интервале (xi, xi+l) лет из числа доживающих до точного возраста xi+1лет рассчитываются по формулам:
di = l iqi; иli+1 = li - di, где i=0, 1, 2, 3,..., w - 1.
Число человеко-лет, прожитых на возрастном интервале (xi, xi+l) лет, или число живущих на этом интервале, при принятии гипотезы линейности равно: Li = ni(li - di) + ai ni di, гдеi= 0,1,2, 3,..., w - 1. Если же принимается экспоненциальная гипотеза, то для возрастного интервала 0 - 1 год используется альтернативная формула.
И для возрастного интервала 1 - 4 года:
Похожие работы
... у мужчин. Эта точка зрения подкрепляется фактами существования чемпионов-долгожителей, которые чаще встречаются среди мужчин. Особый интерес для изучения проблемы старения и продолжительности жизни представляет разностороннее изучение долгожителей как людей с оптимальным состоянием важнейших физиологических функций. Долгожительскими считаются популяции, в которых отношение числа лиц старше 90 ...
... в средней продолжительности жизни в европейских странах и развивающихся странах Азии Африки и Латинской Америки. Низкая продолжительность жизни во многих странах Африки и Азии - наследие длительного колониального режима со всеми его последствиями: низким уровнем материального обеспечения, нищетой, голодом или недоеданием, плохими жилищными и санитарно-гигиеническими условиями, тяжким физическим ...
... Показатель смертности составил 15,1 человека на 1000 населения; это выше, чем в целом по ДФО (13,7), по Российской Федерации этот показатель составил 14,7 промилле. Для того, что бы проанализировать статистику смертности в Амурской области, в первую очередь требуется рассмотреть коэффициент смертности населения. Общий коэффициент смертности является демографическим коэффициентом, показывает число ...
... стандарты лечения, создать систему персонифицированного учета медицинской помощи, перевести лечебные учреждения на оплату по конечному результату. ГЛАВА III. ОСНОВНЫЕ НАПРАВЛЕНИЯ ДЕЯТЕЛЬНОСТИ РЕСПУБЛИКАНСКИХ ОРГАНОВ ВЛАСТИ ПО СНИЖЕНИЮ СМЕРТНОСТИ В ЧУВАШСКОЙ РЕСПУБЛИКЕ 3.1 Реализация региональной демографической политики в Чувашской Республике В наше время решение демографических проблем ...


0 комментариев