Б) построить в масштабе графики рассчитанных закона и функции распределения вероятностей

5. б) построить в масштабе графики рассчитанных закона и функции распределения вероятностей

График закона распределения вероятностей имеет вид:

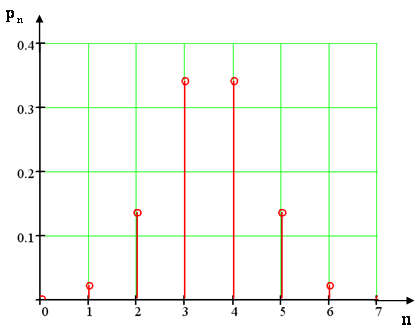
Рис. 7

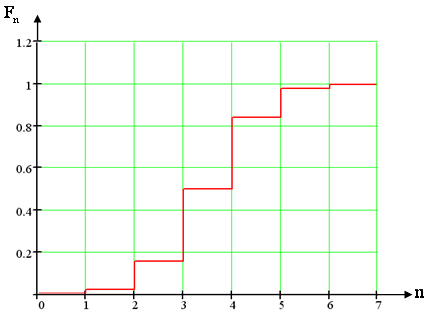График функции

распределения вероятностей имеет вид:

 Рис.8
6. Закодировать значения L-ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний кода

При организации цифровой связи широкое распространение получило двоичное кодирование, когда кодовые символы могут принимать только два значения:  и . Процедура двоичного безызбыточного блочного кодирования отсчетов  состоит в следующем: физические уровни , где , вначале перенумеровываются, то есть заменяются их номерами , иначе говоря, представляются в виде десятичных чисел от 0 до L–1. Затем эти десятичные числа представляются в двоичной системе счисления с основанием 2. Это представление имеет вид:

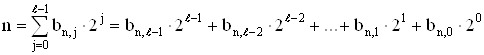, где  –

двоичный кодовый символ (0 или 1) десятичного числа n, расположенный в j-й позиции кодовой комбинации

; .

По условию, , значит . Получим:

.

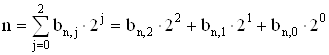Следовательно, в конечном счете, получаем кодовые комбинации кода:

Таким образом, в моменты времени ,  уровни  переводятся в числа n, которые, в свою очередь, переводятся в кодовые комбинации , . В результате образуется сигнал импульсно-кодовой модуляции (ИКМ).

Кодовым расстоянием  между двумя двоичными кодовыми комбинациями  и  называется количество позиций, в которых одна кодовая комбинация отличается от другой. Таблица кодовых расстояний строится по формуле: , где  – соответственно, строка и столбец этой таблицы;  – суммирование по модулю два: , , , .

Построим таблицу кодовых расстояний:

	000	001	010	011	100	101	110	111
000	0	1	1	2	1	2	2	3
001	1	0	2	1	2	1	3	2
010	1	2	0	1	2	3	1	2
011	2	1	1	0	3	2	2	1
100	1	2	2	3	0	1	1	2
101	2	1	3	2	1	0	2	1
110	2	3	1	2	1	2	0	1
111	3	2	2	1	2	1	1	0

 Таблица 8

 а) рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ

Так как среднее число нулей  и среднее число единиц  в сигнале ИКМ одинаково (что справедливо для гауссовского сообщения и данного способа кодирования), то и вероятности их появления одинаковы: .

На интервале дискретизации T при блочном безызбыточном кодировании должно уместиться  элементарных кодовых символов, следовательно, их длительность равна . Ширина спектра элементарного прямоугольного импульса обратно пропорциональна длительности .

Поэтому начальная ширина спектра сигнала ИКМ равна:

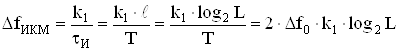, где  –

постоянная, а. После вычислений получим:

.

б) изобразить качественно на одном графике сигналы в четырех сечениях АЦП: вход АЦП, выход дискретизатора, выход квантователя,

выход АЦП.АЦП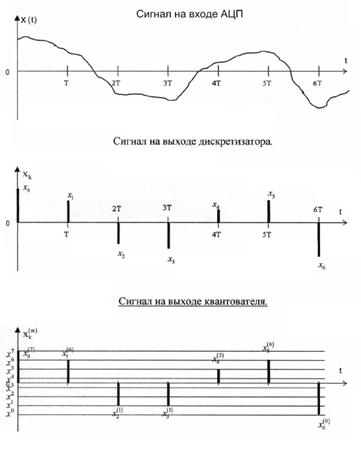

Рис.9

7. Полагая, что для передачи ИКМ сигнала по непрерывному каналу связи (НКС) используется гармонический переносчик:

 

 а) рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра:

Для передачи ИКМ сигнала по НКС используется гармонический переносчик, который можно записать в виде: , где  – амплитуда,  – частота (по условию ),  – начальная фаза (примем равной нулю). В качестве модели модулирующего импульсного сообщения  примем тригонометрический ряд вида:

.

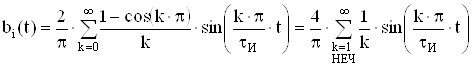Отсюда следует, что это сообщение имеет только нечетные гармонические составляющие на частотах , .

Сигнал дискретной относительной фазовой модуляции представляется в виде:

.

m_фм=π/2 -индекс фазовой модуляции(максимальное отклонение фазы сигнала ДОФМ от фазы несущей)

Подставив в это соотношение , получим следующее спектральное разложение сигнала дискретной амплитудной модуляции:

Из выражения видим, что спектр сигнала будет содержать гармоники на частотах  и  , где k - 1,

 

-частота следования элементарных импульсов

Начальная ширина спектра сигнала:

Для вычисления нормированного спектра будем рассчитывать нормированные значения амплитуд гармоник:

 б) построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нем найденную ширину спектра

 

Таблица значений нормированных амплитуд гармоник:

-9	1.302	1.098	0.071
-7	1.279	1.121	0.09
-5	1.256	1.143	0.12
-3	1.234	1.166	0.21
-1	1.211	1.189	0.63
0	1.2	1.2	0
1	1.189	1.211	0.63
3	1.166	1.234	0.21
5	1.143	1.256	0.12
7	1.121	1.279	0.09
9	1.098	1.302	0.071

Таблица 9

Построим график нормированного спектра сигнала дискретной модуляции, на котором покажем ширину спектра сигнала ДОФМ:

∆fДОФМ

Рис. 10

8. Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал-шум:

а) рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала и пропускную способность НКС

Помеха, имеющая равномерный энергетический спектр от 0 до  (), называется белым шумом. Мощность гауссовского белого шума в полосе пропускания полосового фильтра геометрически определяется как площадь прямоугольника с высотой  и основанием :

,

где  – постоянная энергетического спектра шума НКС,  – ширина спектра сигнала ДОФМ.

Учитывая то, что начальное отношение сигнал-шум (ОСШ)  на входе детектора приемника известно, найдем мощность сигнала дискретной модуляции, обеспечивающего необходимое соотношение сигнал-шум на входе приемника:

.

Мощность сигнала ДОФМ и амплитуда, в среднем приходящаяся на один двоичный символ:

-мощность сигнала ДОФМ на один двоичный символ.

-амплитуда сигнала ДОФМ на один двоичный символ.

Пропускная способность характеризует максимально возможную скорость передачи информации по данному каналу. Пропускная способность гауссовского НКС определяется по формуле:

.

 

б) построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП

ФПВ мгновенных значений УГП имеют вид гауссовского распределения с числовыми характеристиками: нулевым математическим ожиданием и дисперсией (мощностью) .

ФПВ мгновенных значений УГП задается соотношением вида:

.

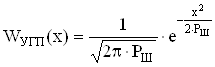ФПВ мгновенных значений суммы гармонического сигнала с УГП равна:

.

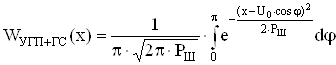Построим графики полученных выражений для ФПВ мгновенных значений УГП и суммы гармонического сигнала и УГП:

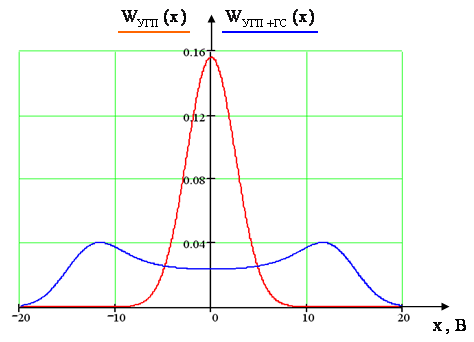1/В

Рис. 11

Огибающая гауссовской помехи распределена по закону Рэлея:

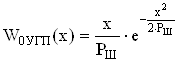, при .

Огибающая суммы гармонического сигнала и УГП подчиняется обобщенному распределению Рэлея (распределению Райса):

, при ,

где  – модифицированная функция Бесселя нулевого порядка от мнимого аргумента.

Построим графики полученных выражений для огибающих УГП и суммы гармонического сигнала и УГП:

1/В

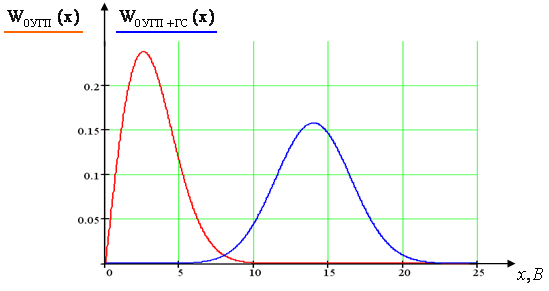
 Рис.12

9. С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:

 а) рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС

За количественную меру помехоустойчивости в системах электросвязи принимается средняя на бит вероятность ошибки:

, где  и  – безусловные (априорные) вероятности передачи 1 и 0.

При равенстве априорных вероятностей , а также условных вероятностей  (условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна .

Условные вероятности ошибок находятся интегрированием условных ФПВ отклика детектора:

;

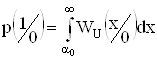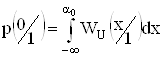 , где  и  –

соответственно, ФПВ отклика детекторов при условии формирования на передаче в сигнале ИКМ 0 или 1;

 – пороговое напряжение.

Гауссовские ФПВ отклика детектора имеют вид:

; .

Для симметричного ДКС .

Средняя вероятность ошибки в двоичном ДКС:

Скорость передачи информации по двоичному симметричному ДКС, когда

,

определяется по формуле:

,

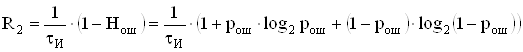где  – энтропия ошибочных решений.

 

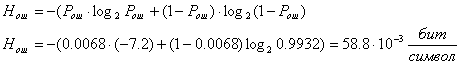
Получим:

.

Так как вероятности ошибок  для различных видов сигналов зависят от ОСШ  на входе детектора, то и скорость передачи информации зависит от ОСШ. Для сравнения скорости  при данном виде модуляции и способе приема с пропускной способностью НКС  вводят показатель эффективности, вычисляемый из отношения:

.

Эффективность высока при  и низка при .

 б) изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи, когда он выносит ошибочные решения

Схема приемника сигналов ДОФМ-СФ имеет вид:

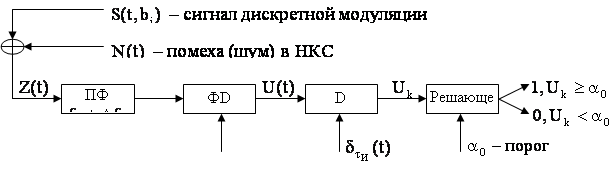
Рис. 13

В сигналах с фазовой модуляцией (ФМ), знак выходного напряжения определяется фазой принятого сигнала в фазовом детекторе ФD.

При способе сравнения фаз(СФ), за счет линии задержки(ЛЗ) ОДФМ сигнал задерживается на время посылки τ_з= τ_и, совмещаются n-ая и (n-1)-ая посылки. Их фазы сравниваются в ФD. В результате восстанавливается сигнал с модуляцией по закону управляющих напряжений. К дискретизатору (D), подводится отклик детектора U(t), а так же последовательность дискретизирующих импульсов с периодом τ_и , которые необходимы для взятия одного отсчёта в середине посылки длительностью τ_и.

В решающем устройстве( РУ) отсчеты U_K сравниваются с α₀, и принимается решение передана 1, если фаза равна «+π/2»; и передан 0, если фаза равна

«-π/2». Под действием помех в канале связи амплитуда сигнала изменяется, и решающее устройство(РУ) может ошибаться, при передаче 0, принимать 1 или при передаче 1, принимать 0.

 

10. Рассматривая отклик декодера ПРУ как случайный дискретный сигнал на выходе L-ичного ДКС:

 а) рассчитать распределение вероятностей дискретного сигнала на выходе декодера, скорость передачи информации по L-ичному ДКС, относительные потери в скорости передачи информации по L-ичному ДКС.

 

Распределение вероятностей дискретного сигнала на выходе детектора определяется выражением:

, где m=.

В этом выражении  – вероятность ошибки в двоичном симметричном ДКС (найдена в пункте 9. а);  – вероятность правильного приема двоичного символа, причем ;  – найденный в пункте 5.а) закон распределения вероятностей квантованного сигнала. Получим:

n	0	1	2	3	4	5	6	7
	0.00135	0.0214	0.136	0.341	0.341	0.136	0.0214	0.00135
	0.0047	0.024	0.136	0.335	0.335	0.136	0.024	0.0047

Таблица 10

Для определения скорости передачи информации по L-ичному ДКС воспользуемся соотношением:

,

где  – энтропия ошибочных решений

 –

энтропия восстановленного L-ичного сообщения;

  – частота дискретизации отклика ИФНЧ.

Получаем:

 .

Зная производительность L-ичного источника (скорость ввода информации в ДКС)  и скорость передаваемой по ДКС информации, находим величину относительных потерь в скорости:

.

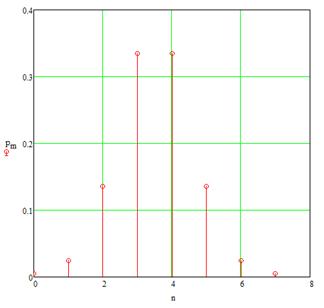
б) построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя.

График закона распределения вероятностей отклика детектора имеет вид:

	Рис. 14

Сравнивая полученный график с найденным в пункте 5.б), видно, что вид графиков совпадает, численные отклонения можно проследить по таблице в пункте 10.а).

11. Полагая ФНЧ на выходе ЦАП приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения:

 

 а) рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шума передачи (СКПП), суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП).

Дисперсия случайных импульсов шума передачи на выходе интерполятора ЦАП определяется по формуле:

,

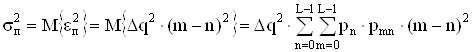где  – найденное значение шага квантования, для расчета перейдем к постоянной усредненной величине вероятности ошибки передачи:

; ;

 – вероятность правильного приема двоичного символа; .

Вычислим .

Подставив в формулу, найдем:

 .

Вычислим среднюю квадратическую погрешность шума передачи (СКПП):

, где  – энергетический спектр шума передачи.

.

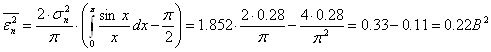В виду того, что погрешность фильтрации , шум квантования  и шум передачи  являются независимыми случайными процессами, то суммарная СКП восстановления непрерывного сообщения будет равна сумме СКП указанных процессов:

.

Тогда относительная суммарная СКП (ОСКП) восстановления сообщения равна:

.

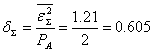б) Качественно изобразить сигналы на выходе декодера и интерполятора ЦАП, а также восстановленное сообщение на выходе системы электросвязи.

Список использованной литературы

1.  Зюко А.Г., Кловский Д.Д. и др. Теория электрической связи. Учебник для вузов. – М.: Радио и связь, 1998. – 432 с.

2.  Санников В.Г. Методические рекомендации по выполнению курсовой работы. – М., 1996. – 40 с.

3.  Конспект лекций.