Навигация
Загальне (часове) рівняння Шредінгера
1.2.2 Загальне (часове) рівняння Шредінгера
У класичній механіці рівняння одновимірного руху частинки дозволяє одержати її координату x(t) і імпульс p(t) за їх початковими значеннями x(0) і p(0). Таким рівнянням руху є другий закон Ньютона.
![]() (1.2.11)
(1.2.11)
де m ― маса частинки; ![]() ― прискорення руху частинки;
― прискорення руху частинки; ![]() ― градієнт потенціальної енергії, зміна якої визначається діючою силою.
― градієнт потенціальної енергії, зміна якої визначається діючою силою.
З визначення квантового стану рівняння руху квантової частинки має задавати зміну в часі хвильової функції ![]() . Оскільки квантовий стан характеризує лише одна хвильова функція, то відповідне квантове рівняння руху повинно містити лише першу похідну за часом від хвильової функції. В інших випадках таке рівняння не буде погоджуватись з визначенням квантового стану .
. Оскільки квантовий стан характеризує лише одна хвильова функція, то відповідне квантове рівняння руху повинно містити лише першу похідну за часом від хвильової функції. В інших випадках таке рівняння не буде погоджуватись з визначенням квантового стану .
Рівняння руху квантової нерелятивістської частинки в силовому полі називається рівнянням Шредінгера, тому що вперше в 1926 році воно було сформульовано німецьким фізиком Е. Шредінгером.
Справедливість цього рівняння обґрунтована тим, що всі висновки які випливають із нього, знайшли своє експериментальне підтвердження. Рівняння Шредінгера відіграє у квантовій механіці таку ж роль, як і рівняння Ньютона в класичній.
У загальному випадку часове рівняння Шредінгера має вигляд![]() (1.2.12)
(1.2.12)
де m ― маса частинки; ![]() ― потенціальна енергія частинки в сило-вому полі;
― потенціальна енергія частинки в сило-вому полі; ![]() ― уявна одиниця;
― уявна одиниця; ![]() ― стала Дірака;
― стала Дірака; ![]() ― оператор Лапласа.
― оператор Лапласа.
Через присутність в рівнянні Шредінгера (1.2.12) уявної одиниці хвильова функція ![]() , яка задовольняє це рівняння, завжди комплексна. Не кожна функція може бути розв’язком рівняння (1.2.12). Перш за все ця функція повинна бути скінченною, неперервною і мати неперервні перші похідні. Ці вимоги мають чисто математичний характер. Крім того ─ хвильова функція повинна бути однозначною, інакше буде порушений її статистичний зміст.
, яка задовольняє це рівняння, завжди комплексна. Не кожна функція може бути розв’язком рівняння (1.2.12). Перш за все ця функція повинна бути скінченною, неперервною і мати неперервні перші похідні. Ці вимоги мають чисто математичний характер. Крім того ─ хвильова функція повинна бути однозначною, інакше буде порушений її статистичний зміст.
Рівняння Шредінгера за часом є лінійним диференціальним рівнянням 1-го порядку. З теорії диференціальних рівнянь відомо, що кожне лінійне рівняння в частинних похідних повинно мати безліч розв’язків, причому таких, що всяка лінійна комбінація будь-якої сукупності розв’язків теж буде його розв’язком.
Слід зауважити, що рівняння Шредінгера, подібно до законів Ньютона в класичній механіці, не є результатом якогось теоретичного доведення, а є узагальненням багатьох дослідних фактів, встановлених при вивченні мікросвіту. Відмітимо також, що рівняння Шредінгера описує рух частинок, швидкість яких значно менша швидкості світла, оскільки співвідношення між кінетичною енергією й імпульсом справедливе лише при цих умовах. У релятивістському випадку для описання хвильових властивостей мікрочастинок слід користуватись іншими рівняннями, наприклад рівняннями Дірака або Клейна ― Гордона.
1.2.3 Рівняння Шредінгера для стаціонарних станів
Потенціальна енергія частинки залежить від координат x, y, z і часу t. Якщо потенціальна енергія U від часу не залежить і відповідно повна енергія також не змінюється з часом, то хвильову функцію ![]() можна подати у вигляді добутку двох співмножників
можна подати у вигляді добутку двох співмножників
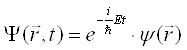 . (1.2.13)
. (1.2.13)
Перший співмножник в (1.2.13) залежить лише від часу, а другий ― лише від координат (![]() ).
).
Розв’язки рівняння Шредінгера, а також стани частинок, для яких потенціальна енергія, а також густина імовірностей не змінюються з часом, називаються стаціонарними. Стаціонарні стани не виключають залежності хвильової функції від часу, а лише обмежують її гармонічним законом ![]() .
.
Підставляючи хвильову функцію (1.2.13) у рівняння Шредінгера (1.2.12) одержимо
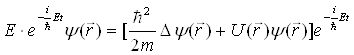 .
.
Скоротимо цей вираз на експоненту:
![]() , (1.2.14)
, (1.2.14)
де 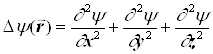 ; Е ― повна енергія частинки;
; Е ― повна енергія частинки; ![]() ― потенціальна енергія частинки, яка є функцією лише координат;
― потенціальна енергія частинки, яка є функцією лише координат; ![]() ― хвильова функція; m ― маса частинки;
― хвильова функція; m ― маса частинки; ![]() ― стала Дірака (
― стала Дірака (![]() ).
).
Стаціонарне рівняння Шредінгера (1.2.14) є однорідним лінійним диференціальним рівнянням другого порядку відносно координат x, y, z. У випадку, коли ![]() =0, це рівняння не має фізичного змісту. У рівнянні Шредінгера для стаціонарних станів є єдиний вільний параметр ― повна енергія частинки Е. При деяких значеннях повної енергії це рівняння може мати нульові розв’язки. Ті значення повної енергії, при яких рівняння (1.2.14) буде мати нульові розв’язки, називаються власними значеннями. Кожному такому власному значенню енергії відповідає свій розв’язок рівняння (1.2.14).
=0, це рівняння не має фізичного змісту. У рівнянні Шредінгера для стаціонарних станів є єдиний вільний параметр ― повна енергія частинки Е. При деяких значеннях повної енергії це рівняння може мати нульові розв’язки. Ті значення повної енергії, при яких рівняння (1.2.14) буде мати нульові розв’язки, називаються власними значеннями. Кожному такому власному значенню енергії відповідає свій розв’язок рівняння (1.2.14).
Стаціонарне рівняння Шредінгера дає не лише значення хвильової функції, але й значення цієї функції у стаціонарних станах.
Похожие работы
... для систем, частинок з антисиметричними хвильовими функціями, тобто до ферміонів. 2.2.3. Розподіл електронів за станами. Періодична система елементів. Сукупність електронів, які перебувають у всіх можливих станах з однаковим значенням головного квантового числа n, утворює електронну оболонку (електронний шар). Енергетичні шари прийнято позначати великими латинськими літерами відповідно до ...
... ію грунтується дія ядерних реакторів. Термоядерні реакції – вид ядерних реакцій, що відбуваються при високих температурах: Квантово-механічне пояснення будови молекул Вчення про хімічний зв’язок – центральна проблема сучасної хімії. Незнаючи природу взаємодії атомів у речовині не можна зрозуміти механізм утворення хімічних сполук, їх склад, будову і реакційну здатність. Сукупність ...
... яка була накопичена до п'ятидесятих років у радіочастотній й оптичній спектроскопії і які згодом отримали своє використання у квантовій електроніці. Розділ 2. Основні поняття квантової електроніки (фізичні основи квантової електроніки) Принцип дії лазера або мазера заснований на трьох «китах» – головних поняттях квантової електроніки, а саме на поняттях вимушеного випромінювання, інверсного ...
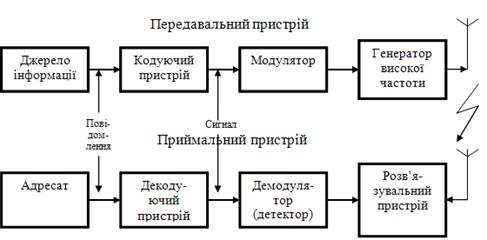
... Сигнал як матеріальний носій інформації є певною змінною у часі фізичної величини (напруги, струму, заряду, магнітного потоку тощо). 3 інформаційного погляду всю розмаїтість сигналів можна розділити на дві основні групи: детерміновані та випадкові. Детермінованими називають сигнали, значення яких у будь-який момент часу є точно відоме, тобто їх можна передбачити безпомилково. Такі сигнали не ...


0 комментариев