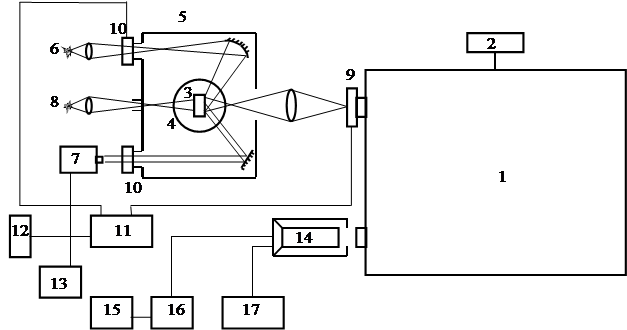
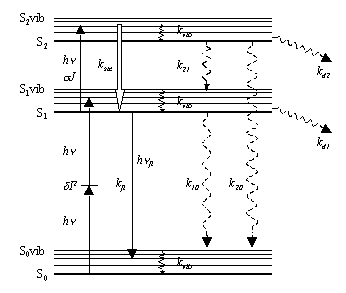
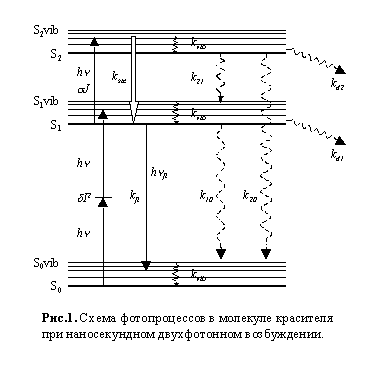
Навигация
Обработка полученных данных
3.1. Обработка полученных данных.
Ранее установлено, что отжиг раствора для многих донорно-акцепторных пар может приводить к увеличению интенсивности фосфоресценции как донора, так и акцептора и к уменьшению времени затухания.
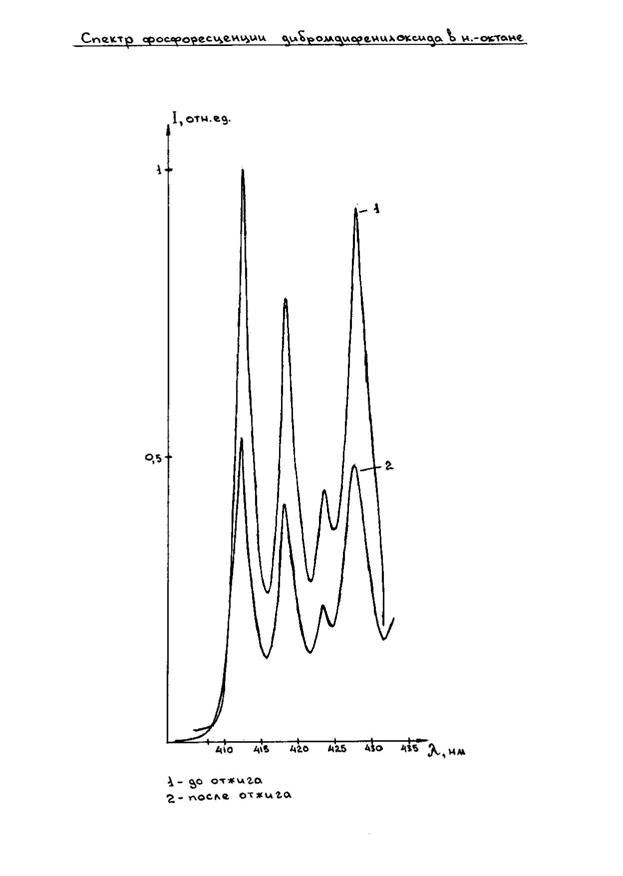
Результаты исследования влияния отжига на фосфоресценцию донора представлены на рис.3.1. График 1 характеризует фосфоресценцию дибромдифенилоксида до отжига, график 2 – после отжига. Из рисунка видно, что интенсивность фосфоресценции после отжига уменьшилась примерно в 2 раза, чем до отжига.
Так как были получены данные, что интенсивность фосфоресценции акцептора уменьшилась после отжига (причем в большее число раз нежели донора), то представляло особый интерес исследование сенсибилизированной фосфоресценции акцептора.
Полученные данные по фосфоресценции донорно-акцепторной смеси, а так же по времени затухания акцептора сведены в табл.3.1.
Табл.3.1. Влияние отжига на параметры фосфоресценции компонент донорно-акцепторной смеси дибромдифенилоксида и аценафтена в н.-октане.
| донор | акцептор | ||
| I/I0 | I/I0 | τ/τ0 | |
| До отжига | 1 | 1 | 1 |
| После отжига | 0,55 | 0,32 | 0,79 |
Рис.3.1.
Обозначим интенсивность сенсибилизированной фосфоресценции после быстрого замораживания образца до 77 К через I(0). После отжига образца в течение определённого времени t при температуре Т и последующем охлаждении до 77 К интенсивность сенсибилизированной фосфоресценции обозначим через I(t). Тогда DI(t) = I(t) – I(0) – означает прирост интенсивности сенсибилизированной фосфоресценции в процессе отжига образца в течение этого времени.
Можно предположить, что при фиксированной температуре Т прирост интенсивности DI(t) в зависимости от времени отжига происходит по закону, определяемому экспонентой:
DI(t) = DI(¥){1-exp(-t/t)}, (3.1)
с характерным временем t, которое зависит от температуры отжига. DI(¥) - прирост интенсивности при длительном отжиге образца - t »t.
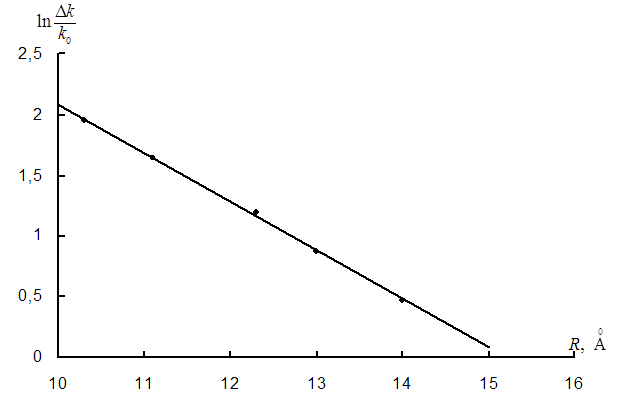
Экспериментально эта зависимость была проверена в данной работе для пары дибромдифенилоксид-аценафтен в н.-октане. На рис. 3.2 представлен график зависимости [DI(t) - DI(¥)]/DI(¥) от t в полулогарифмическом масштабе.
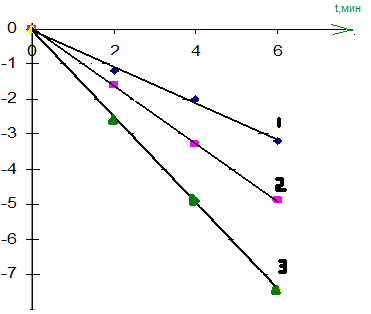
Рис. 3.2. Зависимость интенсивности сенсибилизированной фосфоресценции аценафтена, донор – дибромдифенилоксид, в н.-октане от времени отжига при температурах: 1 – 167 К, 2 – 180 К, 3 – 195 К; СД=1.25×10-3М , СА=1.25×10-3М; z = ln [(DI(¥)-DI(t))/DI(¥)].
Как видно из рисунка, экспериментальные точки хорошо укладываются на экспоненту (сплошная линия) с различными углами наклона, определяемыми температурой отжига. Величина, обратная тангенсу угла наклона прямых, соответствует характерному времени t процесса при данной температуре отжига. Для всех исследованных систем повышение температуры отжига раствора приводит к уменьшению характерного времени процесса нарастания.
Табл.3.1. Характерное время t процесса нарастания числа одиночных молекул акцептора, участвующих в переносе энергии в процессе отжига.
| Тотж, К | q, 1/мин | |
| Дибромдифенилоксид-аценафтен в н.-октане | 167 | 0,48 |
| 180 | 0,71 | |
| 195 | 1,67 |
Выше было показано, что в твёрдом теле подобные физические и химические процессы обычно характеризуются Аррениусовской зависимостью константы скорости процесса от температуры:
q(Т) = q(¥) ехр (-Еак/RT) (3.2)
где q(¥) - предэкспоненциальный множитель, Еак- энергия активации процесса.
Соответственно для t :
t(Т) = (1/ q(¥)) ехр (Еак/RT). (3.3)
Представляло интерес экспериментально проверить эту зависимость.
Прологарифмируем уравнение Аррениуса (48):
lnt = Еак/RT- ln [q(¥)]. (3.4)
Написав это уравнение для различных температур Т1 и Т2 и вычтя второе уравнение из первого, получим:
ln(t1/t2)= Еак/R (1/T1- 1/Т2). (3.5)
Если это уравнение справедливо, то на графике в координатах ln(t1/t) от (1/T1- 1/Т) экспериментальные точки должны располагаться на прямой с тангенсом угла наклона, равным Еак/R.
На рис. 3.3 представлена данная зависимость для пары дибромдифенилоксид-аценафтен в н.-октане. Как видно из рисунка, экспериментальные точки хорошо укладываются на экспоненту (сплошная линия). Это говорит об экспоненциальной зависимости характеристического времени процесса t от температуры. Следовательно, и константа скорости q физического процесса, происходящего при отжиге экспоненциально растёт с повышением температуры.
Таким образом, на основании этих экспериментальных данных можно утверждать, что физический процесс, приводящий к увеличению числа участвующих в переносе энергии мономерных молекул акцептора при отжиге описывается Аррениусовской зависимостью константы скорости процесса от температуры.
Величина тангенса угла наклона прямых q позволяет определить энергию активации процесса: Еак= R tgq.
ln(τ1/τ)
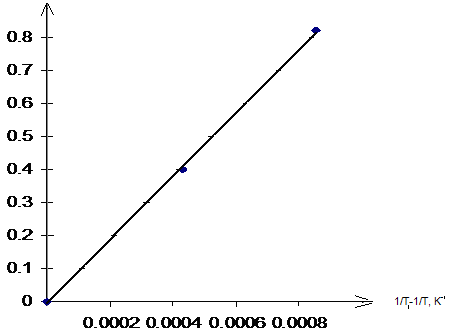
Рис.3.3. Зависимость характеристического времени процесса от температуры, для донорно-акцепторных пары дибромдифенилоксид-аценафтен в н.-октане (СД=1.25×10-3М, СА=1.25×10-3М).
Энергия активации этого процесса для данной донорно-акцепторной пары представляет величину 9 кДж/моль.
Похожие работы
... основном состоянии на вероятность излучательной дезактивации энергии триплетного возбуждения в акцепторе показали следующее. Такое взаимодействие увеличивает вероятность дезактивации триплетных молекул акцептора в системах для которых. При этом константа скорости излучательного перехода экспоненциально увеличивается с уменьшением среднего расстояния между компонентами донорно-акцепторной смеси. ...
... (47) Величина, обратная t, характеризует скорость прироста при данной температуре концентрации триплетных молекул акцептора энергии, q = 1/t , и называется константой скорости процесса [161]. Итак, прирост в результате отжига образца числа молекул, участвующих в излучении сенсибилизированной фосфоресценции происходит по экспоненциальному закону. Константа скорости этого ...
... , что опасность тушения веществами, которая появляется в методе внутреннего стандарта сильно переоценивается Персоновым и Теплицкой. Из всего вышесказанного ясно, что методы спектрального анализа нашли самое широкое применение и в медицине и в нефтеперерабатывающей промышленности и в фундаментальных исследованиях. Поэтому важную роль при использовании спектров органических соединений играет их ...







0 комментариев