Навигация
Радиогеохимический эффект можно применять при исследованиях в интервале пластов, не вскрытых перфорацией
5. Радиогеохимический эффект можно применять при исследованиях в интервале пластов, не вскрытых перфорацией.
2. Основные уравнения
Содержанием этой главы являются основные понятия и уравнения, и их решения, необходимые разработки теории на основе математической модели.
2.1. Уравнение неразрывностиВ замкнутой изолированной системе полная масса остается постоянной, т.е. она не возникает и не исчезает сама по себе.
Закон сохранения массы означает, что для любого ![]() с поверхностью
с поверхностью ![]() изменение массы в
изменение массы в ![]() должно равняться количеству массы протекающему через
должно равняться количеству массы протекающему через ![]() .
.
Плотностью ![]() в точке
в точке ![]() пространства называют предел отношения массы
пространства называют предел отношения массы ![]() в элементарном объеме
в элементарном объеме ![]() этому объему, охватывающему точку
этому объему, охватывающему точку ![]() , при стягивании его в эту точку, т.е.:
, при стягивании его в эту точку, т.е.:
|
| (2.1) |
Тогда
|
| (2.2) |
где m - интегральный параметр, удовлетворяющий закону аддитивности, ![]() -локальный параметр.
-локальный параметр.
Выделим в пространстве неподвижную замкнутую поверхность ![]() ограничивающую объем
ограничивающую объем ![]() . Каждой точке выделенного объема
. Каждой точке выделенного объема ![]() сопоставим вектор
сопоставим вектор ![]() .
.
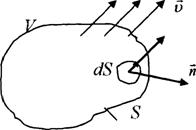
Рис.3.
Выберем на поверхности ![]() ориентированный элемент поверхности, где
ориентированный элемент поверхности, где ![]() – вектор внешней нормали,
– вектор внешней нормали, ![]() - площадь выбранной площадки.
- площадь выбранной площадки.
Тогда через элемент площади ![]() входит или выходит количество массы сплошной среды
входит или выходит количество массы сплошной среды ![]() , где
, где ![]() – вектор потока массы.
– вектор потока массы.
Через всю поверхность войдет или выйдет количество массы
|
| (2.3) |
Будем предполагать, что источники и стоки отсутствуют, тогда закон сохранения массы запишется в виде:
|
| (2.4) |
В (2.4) знак минус в правой части объясняется тем, что если ![]() образует с
образует с ![]() острый угол, т.е.
острый угол, т.е.![]() , то
, то ![]() проходит через
проходит через ![]() изнутри наружу, т.е. масса в
изнутри наружу, т.е. масса в ![]() убывает.
убывает.
|
| (2.5) |
Уравнение (2.5) – уравнение неразрывности для массы в интегральной форме.
Проведем в первом интеграле (2.5) дифференцирование по ![]() как по параметру (поскольку
как по параметру (поскольку ![]() не зависит от
не зависит от ![]() ), т.е. внесем производную под знак интеграла и заменим ее частной производную, поскольку подынтегральная функция
), т.е. внесем производную под знак интеграла и заменим ее частной производную, поскольку подынтегральная функция ![]() зависит от переменной интегрирования, получим:
зависит от переменной интегрирования, получим:
|
| (2.6) |
Второй интеграл в равенстве (2.5) преобразуем в объемный, воспользовавшись теоремой Остроградского-Гаусса. Получим
|
| (2.7) |
где
|
|
Подставим (2.6), (2.7) в (2.5), и объединяя интегралы получим
|
| (2.8) |
Учитывая в (2.8) произвольность объема ![]() , получаем
, получаем
|
| (2.9) |
Уравнение (2.9)– уравнение неразрывности для массы в дифференциальной форме.
2.2. Закон Фика
Закон Фика необходим для описания диффузии растворенного(радиоактивного) вещества пропорциональной градиенту их плотности. Плотность радиоактивных примесей является функцией от химического потенциала ![]()
В уравнении (2.9) предыдущего параграфа вектор потока имеет вид
|
| (*) |
где ![]() – конвекционная компонента вектора потока, связанная с потоком вещества (массы). Для случая, когда движение массы происходит только за счет конвекции, поток записывается в виде
– конвекционная компонента вектора потока, связанная с потоком вещества (массы). Для случая, когда движение массы происходит только за счет конвекции, поток записывается в виде
|
| (2.10) |
![]() – диффузионная компонента, возникает при наличии в системе градиента концентрации. Для диффузионного компонента справедлив I Закон Фика:
– диффузионная компонента, возникает при наличии в системе градиента концентрации. Для диффузионного компонента справедлив I Закон Фика:
|
| (2.10*) |
![]() – коэффициент концентрационной диффузии, (далее
– коэффициент концентрационной диффузии, (далее ![]() будем опускать).
будем опускать).
Диффузионный поток пропорционален градиенту плотности, взятому с обратным знаком.
Подставим (2.10) и (2.10*) в (*), получим
|
| (2.11) |
Подставим (2.11) в (2.9), получим
|
| (2.12) |
В (2.12) каждое слагаемое записали отдельно:
|
|
Преобразуем второе слагаемое в (2.12):
|
| (2.13) |
Во втором слагаемом в (2.13) осуществим круговую перестановку (знак не меняется, т.к. скалярное произведение).
Из выражения (2.13), получим
|
| (2.14) |
Преобразуем второе слагаемое в (2.12):
|
|
Условие не сжимаемости жидкости:
|
| (2.15) |
Подставив (2.14) и (2.15) в (2.12) получим
|
| (2.16) |
Если в (2.16) то получим уравнение диффузии (II Закон Фика):
|
| (2.17) |
2.3. Уравнение конвективной диффузии
Пусть имеется раствор с плотностью растворителя ![]() и плотностью растворенного вещества –
и плотностью растворенного вещества –![]() , тогда плотность раствора запишется в виде
, тогда плотность раствора запишется в виде
|
| (2.18) |
Запишем уравнение неразрывности для растворителя:
|
| (2.19) |
Диффузию не учитываем, потому что в жидкостях коэффициент диффузии мал.
Будем считать, что растворитель является несжимаемым, т.е. ![]() не зависит от пространственных координат и
не зависит от пространственных координат и
|
| (2.20) |
Тогда из выражения (2.19), получим
|
| (2.21) |
Запишем уравнение неразрывности для раствора:
|
| (2.22) |
В (2.22) подставим (2.18), получим
|
|
Учитывая (2.20), (2.21) и независимость ![]() от пространственных координат, получим
от пространственных координат, получим
|
| (2.23) |
Опустим штрих, предполагая в дальнейшем ![]() – плотность примеси.
– плотность примеси.
|
| (2.24) |
Поясним в (2.24) значение каждого слагаемое:
Первое слагаемое ![]() описывает изменение массового содержания в рассматриваемой точке;
описывает изменение массового содержания в рассматриваемой точке;
Второе слагаемое ![]() отвечает за конвекцию;
отвечает за конвекцию;
Третье слагаемое ![]() отвечает за диффузию.
отвечает за диффузию.
Физический смысл уравнения (2.24) заключается в следующем: изменение концентрации, со временем, в рассматриваемой точке происходит за счет конвекции и диффузии.
На практике в (2.24) слагаемым ![]() можно пренебречь, в силу его малости.
можно пренебречь, в силу его малости.
Пусть движение несущей жидкости происходит вдоль оси ![]() , тогда уравнение без диффузионной конвекции запишется
, тогда уравнение без диффузионной конвекции запишется
|
| (1) |
Одномерное уравнение без диффузионной конвекции (или конвекционное уравнение).
Задача Коши для уравнения (1).
Требуется найти функцию ![]() , где
, где ![]() и удовлетворяющую условиям:
и удовлетворяющую условиям:
|
| (2) |
Получим решение задачи методом характеристик.
Метод характеристик заключается в переходе от эйлеровых переменных ![]() и
и ![]() к лагранжевым. Связь производных в эйлеровых и лагранжевых координатах записывается в виде:
к лагранжевым. Связь производных в эйлеровых и лагранжевых координатах записывается в виде:
|
| (3) |
Уравнение (1) таким образом можно записать как систему двух уравнений:
|
| (4) (5) |
где уравнение (4) – уравнение для характеристик.
Из (5) следует, что ![]() , где
, где ![]() некоторая постоянная. Но т.к.
некоторая постоянная. Но т.к. ![]() , то
, то ![]() .
.
Из (4) получаем
|
| (6) |
Равенство (6) – решение уравнений характеристик.
Интегральные линии уравнения (4) на мировой плоскости ![]() ,
,![]() , т.е. графики движения частиц при заданной скорости
, т.е. графики движения частиц при заданной скорости ![]() , называются характеристиками уравнения (1).
, называются характеристиками уравнения (1).
Пусть при ![]() ,
, ![]() , т.е.
, т.е.
|
| |
|
| (7) |
Подставляя (7) в (2), получим
|
| (8) |
Для того, чтобы получить решение задачи Коши нужно решить систему двух уравнений:
|
| (9) |
|
| (10) |
Подставим уравнение (10) в (9), получим
|
| (11) |
Выражение (11) является решением задачи Коши для уравнения (1).
Решение (11) представляет собой волну бегущую вправо со скоростью ![]() .
.
Начально-краевая задача для уравнения (1) (смешанная задача)
|
| (1) |
|
| (2) |
|
| (3) |
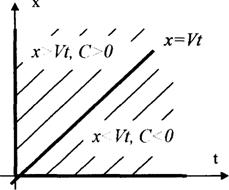
Рис.4.
На рисунке 4 изображены характеристики уравнения (1), где при ![]() начальное условие, а при
начальное условие, а при ![]() граничное условие,
граничное условие, ![]() граничная характеристика.
граничная характеристика.
Для задачи Коши решенной ранее,
|
а)
б) Рис. 5 |
Если |
Получим решение для граничного решения.
|
| (5) |
Запишем уравнения (1) в виде
|
| (6) (7) |
Из (6) следует, что ![]() , где
, где ![]() .
.
Учитывая (3) получим ![]() .
.
Интегрируя (7) получаем
|
| (8) |
Пусть при ![]() ,
, ![]() тогда
тогда
|
| (9) |
Разделим обе части (9) на ![]() получим
получим
|
| (10) |
При ![]() ,
,
|
| (11) |
Подставляя (11) в (3) получаем
|
|
Тогда решая систему
|
|
получаем решение граничной задачи в виде
|
| (12) |
В (12) ![]() .
.
Решение начально-краевой задачи будет иметь вид
|
|
где 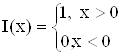 , единичная функция Хевисайда.
, единичная функция Хевисайда.
Решение задачи Коши для неоднородного конвекционного уравнения
Построим формулу Даламбера для уравнения
|
| (1) |
Уравнение (1) – уравнение эволюции локального параметра.
|
| (2) |
Тогда уравнение (1) запишем в виде системы двух уравнений:
|
| (3) (4) |
Интегрируя (4), получим
|
| (5) |
Пусть при ![]() ,
, ![]() , тогда
, тогда
|
|
Подставим (5) в (3), получим
|
| |
|
| (6) |
|
| (7) |
|
| (8) |
Исключим в (6) ![]() для этого учтем начальное условие (7).
для этого учтем начальное условие (7).
|
| |
|
| (9) |
Подставим (9) в (6), получим
|
| |
|
| (10) |
Исключим в (10) ![]() и
и ![]() , потом
, потом ![]() :
:
|
| (11) |
Выражение (11) – формула Даламбера (решение задачи Коши для неоднородного конвекционного уравнения).
Покажем что (11) является решением (1).
Продифференцируем формулу (11) по ![]() , получим
, получим
|
| (12) |
Продифференцируем формулу (11) по ![]() , получим
, получим
|
| (13) |
Подставляя (13) и (12) в (1), получаем
|
|
Откуда получаем тождество: ![]() . Следовательно, выражение (11) является решением уравнения (1).
. Следовательно, выражение (11) является решением уравнения (1).
|
| (1) |
|
| (2) |
|
| (3) |
Найдем решение граничной задачи для неоднородного конвекционного уравнения (1).
Решение будем искать в виде ![]() дифференцируя которое по
дифференцируя которое по ![]() , получим
, получим
|
|
Умножая правую и левую части на ![]() , приходим к выражению
, приходим к выражению
|
| (4) |
Перепишем уравнение (1) в виде двух уравнений:
|
| (5) (6) |
Из (6) следует, что ![]() . Пусть при
. Пусть при ![]() ,
, ![]() , тогда
, тогда ![]() .
.
Откуда получим
|
| (7) |
Подставим уравнение (7) в уравнение (5), получим
|
| |
|
| (8) (9) (10) |
Исключим в (8) ![]() , для этого учтем граничное условие (9).
, для этого учтем граничное условие (9).
|
| |
|
|
Подставим (11) в (8), получим
|
| (12) |
Исключим в (12) ![]() ,
, ![]() и
и ![]() получим
получим
|
| |
|
| (13) |
Выражение (13) – формула Даламбера (решение граничной задачи для неоднородного конвекционного уравнения (1)).
Покажем, что (13) является решением (1). Для этого продифференцируем формулу (13) по ![]() , получим
, получим
|
| (14) |
Продифференцируем формулу (13) по ![]() , получим
, получим
|
| (15) |
Умножая (15) на ![]() и складывая с (14), получим, после сокращений, что
и складывая с (14), получим, после сокращений, что
|
|
то есть, (13) является решением граничной задачи для неоднородного конвекционного уравнения (1).
Решение смешанной задачи запишем, в виде
|
|
2.5 Слабые растворы
Рассмотрим термодинамические свойства слабых растворов, т. е. таких растворов, в которых число молекул растворенных веществ значительно меньше числа молекул растворителя. Рассмотрим сначала случай раствора с одним растворенным веществом; обобщение для раствора нескольких веществ можно будет произвести непосредственно [1].
Пусть ![]() – число молекул растворителя в растворе, а
– число молекул растворителя в растворе, а ![]() – число молекул растворяемого вещества. Концентрацией раствора назовем отношение
– число молекул растворяемого вещества. Концентрацией раствора назовем отношение ![]() ; согласно сделанному предложению
; согласно сделанному предложению ![]() .
.
Найдем выражение для термодинамического потенциала раствора. Пусть ![]() есть термодинамический потенциал чистого растворителя (в котором ничего не растворено). Согласно формуле
есть термодинамический потенциал чистого растворителя (в котором ничего не растворено). Согласно формуле ![]() (справедливой для чистых веществ) его можно написать в виде,
(справедливой для чистых веществ) его можно написать в виде,
|
| (1) |
где ![]() – химический потенциал чистого растворителя. Обозначим посредством
– химический потенциал чистого растворителя. Обозначим посредством ![]() малое изменение, которое испытал бы термодинамический потенциал при введении в растворитель одной молекулы растворяемого вещества. В силу предполагаемой слабости раствора молекулы растворенного вещества в нем находятся на сравнительно больших расстояниях друг от друга, и поэтому их взаимодействие слабо. Пренебрегая этим взаимодействием, можно утверждать, что изменение термодинамического потенциала при введении в растворитель
малое изменение, которое испытал бы термодинамический потенциал при введении в растворитель одной молекулы растворяемого вещества. В силу предполагаемой слабости раствора молекулы растворенного вещества в нем находятся на сравнительно больших расстояниях друг от друга, и поэтому их взаимодействие слабо. Пренебрегая этим взаимодействием, можно утверждать, что изменение термодинамического потенциала при введении в растворитель ![]() молекул растворяемого вещества равно
молекул растворяемого вещества равно ![]() . Однако в получаемом таким путем выражении
. Однако в получаемом таким путем выражении ![]() еще не учтена должным образом одинаковость всех молекул растворенного вещества. Это есть выражение, которое получилось бы по формуле (2), если бы при вычислении статического интеграла все частицы растворенного вещества считались отличными друг от друга. Вычисленный таким образом статический интеграл должен в действительности еще быть поделен на
еще не учтена должным образом одинаковость всех молекул растворенного вещества. Это есть выражение, которое получилось бы по формуле (2), если бы при вычислении статического интеграла все частицы растворенного вещества считались отличными друг от друга. Вычисленный таким образом статический интеграл должен в действительности еще быть поделен на ![]() .
.
|
| (2) |
где ![]() – элемент объема фазового пространства, деленный на
– элемент объема фазового пространства, деленный на ![]() :
:
|
| (3) |
Это приводит к появлению в свободной энергии, а потому и в потенциале ![]() дополнительного члена
дополнительного члена ![]() . Таким образом,
. Таким образом,
|
| (3) |
Далее, поскольку ![]() – само по себе очень большое число, хотя и малое по сравнению с
– само по себе очень большое число, хотя и малое по сравнению с ![]() , в последнем члене можно заменить
, в последнем члене можно заменить ![]() . Тогда
. Тогда
|
| (3) |
Учтем теперь, что ![]() должно быть однородной функцией первого порядка по отношению к
должно быть однородной функцией первого порядка по отношению к ![]() и
и ![]() . Для этого, очевидно, стоящая под знаком логарифма функция
. Для этого, очевидно, стоящая под знаком логарифма функция ![]() должна иметь вид
должна иметь вид ![]() . Таким образом,
. Таким образом,
|
| (3) |
Вводя новую функцию от ![]() и
и ![]() :
:
|
| (3) |
находим окончательно для термодинамического потенциала раствора выражение
|
| (8) |
Сделанное в начале этого параграфа предположение относительно прибавления члена вида ![]() к потенциалу чистого растворителя есть в сущности не что иное, как разложение в ряд по степеням
к потенциалу чистого растворителя есть в сущности не что иное, как разложение в ряд по степеням ![]() с оставлением только первых членов. Член следующего порядка по
с оставлением только первых членов. Член следующего порядка по ![]() пропорционален
пропорционален ![]() , а с учетом однородности по переменным
, а с учетом однородности по переменным ![]() и
и ![]() должен иметь вид
должен иметь вид ![]() , где
, где ![]() – функция только от
– функция только от ![]() и
и ![]() . Таким образом, с точностью до членов второго порядка термодинамический потенциал слабого раствора имеет вид
. Таким образом, с точностью до членов второго порядка термодинамический потенциал слабого раствора имеет вид
|
| (3) |
Обобщение этого выражения на случай раствора нескольких веществ очевидно:
|
| (3) |
где ![]() – число молекул различных растворенных веществ.
– число молекул различных растворенных веществ.
Из (8) легко найти химические потенциалы для растворителя (![]() ) и растворенного вещества (
) и растворенного вещества (![]() ) в растворе:
) в растворе:
|
| (3) |
|
| (12) |
Рассмотрим систему, состоящую из двух соприкасающихся растворов одного и того вещества в различных растворителях (например, в двух несмешивающихся жидкостях). Их концентрации обозначим буквами ![]() и
и ![]() .
.
Условием равновесия этой системы является равенство химических потенциалов растворенного вещества в обоих растворах. С помощью (12, см. 2.5) это условие можно написать в виде
|
| (1) |
Функции ![]() и
и ![]() для различных растворителей, конечно, различны. Отсюда находим
для различных растворителей, конечно, различны. Отсюда находим
|
| (2) |
Коэффициент равновесия растворенного вещества между растворами ![]() есть функция только от
есть функция только от ![]() и
и ![]() . Таким образом, растворенное вещество распределяется между двумя растворителями так, чтобы отношение концентраций было (при заданных давлении и температуре) всегда одинаково, независимо от полного количества растворенного вещества и растворителей (закон распределения). Этот же закон относится, очевидно, и к растворению одного вещества в двух соприкасающихся фазах одного и того же растворителя.
. Таким образом, растворенное вещество распределяется между двумя растворителями так, чтобы отношение концентраций было (при заданных давлении и температуре) всегда одинаково, независимо от полного количества растворенного вещества и растворителей (закон распределения). Этот же закон относится, очевидно, и к растворению одного вещества в двух соприкасающихся фазах одного и того же растворителя.
Далее рассмотрим равновесие между газом (который будем считать идеальным) и его раствором в некотором конденсированном растворителе. Условие равновесия, т.е. равенство химических потенциалов газа чистого и растворенного напишется (с помощью (12) из 2.1.5) в виде
|
| (2) |
откуда
|
| (4) |
Функция ![]() характеризует свойство жидкого (или твердого) раствора; однако при небольших давлениях свойства жидкости очень слабо зависят от давления. Поэтому и зависимость
характеризует свойство жидкого (или твердого) раствора; однако при небольших давлениях свойства жидкости очень слабо зависят от давления. Поэтому и зависимость ![]() от давления не играет роли, и можно считать, что коэффициент при
от давления не играет роли, и можно считать, что коэффициент при ![]() в (4) есть постоянная, не зависящая от давления:
в (4) есть постоянная, не зависящая от давления:
|
| (4) |
Таким образом, при растворении газа концентрация раствора (слабого) пропорциональна давлению(подразумевается, что молекулы газа переходят в раствор в неизменном виде. Если при растворении молекулы распадаются (например, при растворении водорода Н2 в некоторых металлах), то зависимость концентрации от давления получается иной).
2.7. Химический потенциал
Для учета изменения термодинамических функций при изменении количества вещества в системе, необходимо к дифференциалу каждого термодинамического потенциала добавить член ![]() , где
, где ![]() – число частиц вещества в системе, а
– число частиц вещества в системе, а ![]() – коэффициент пропорциональности.
– коэффициент пропорциональности.
В этом случае термодинамические функции будут описывать также и те системы, в которых совершаются процессы с изменением количества вещества.
Например,
|
| (1) |
отсюда
|
| (2) |
где ![]() – тепловая функция, или энтальпия (
– тепловая функция, или энтальпия (![]() ).
).
Так все термодинамические потенциалы имеют размерность энергии, то согласно формуле (2) коэффициент пропорциональности ![]() может быть определен как энергия, отнесенная к одному молю. Этот коэффициент получил название химического потенциала.
может быть определен как энергия, отнесенная к одному молю. Этот коэффициент получил название химического потенциала.
Выражение (1) справедливо для системы, состоящей из однородных молекул. Если же система состоит из разнородных веществ, последний член в формуле (1) надо представить в виде суммы
|
| (3) |
|
| (4) |
характеризует изменение энергии при изменении количества данного компонента вещества в системе на один моль.
Понятно, что химический потенциал можно определить, исходя не только из выражения тепловой функции ![]() (2), но и из выражения любой другой термодинамической функции. При этом по определению
(2), но и из выражения любой другой термодинамической функции. При этом по определению
|
| (5) |
Таким образом, химический потенциал характеризует изменение энергии при изменении количества вещества в системе на один моль.
Похожие работы
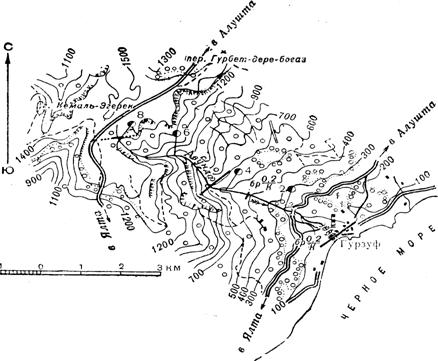
... самого предприятия так как слишком статична и может привести к некоторой неадекватности решений при оперативном их принятии. 2. Экологическая оценка современного состояния гурзуфского парка-памятника садово-паркового искусства Современное экологическое состояние парка можно охарактеризовать как хорошее, но требующее срочных мер по предотвращению воздействия негативных факторов на ...
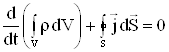
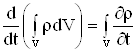
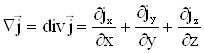
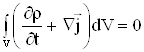
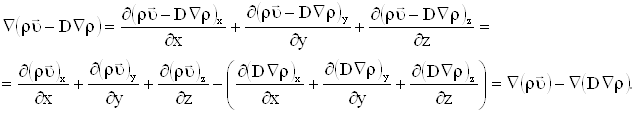
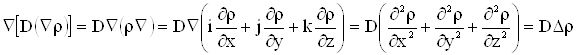
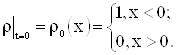

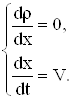
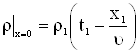 .
.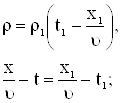
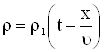 .
.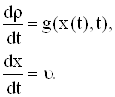
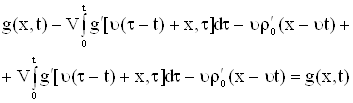 .
.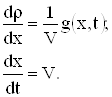
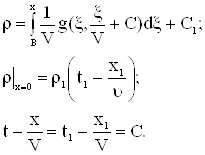
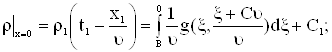
 .
.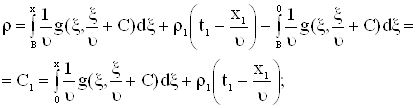
 .
. ,
, .
.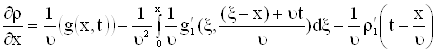 .
.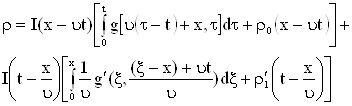 .
. .
.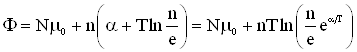 .
.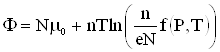 .
.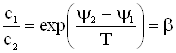 .
.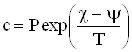 .
.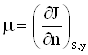 .
.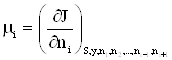
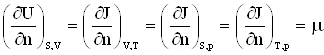 .
.


0 комментариев