Навигация
3.1.1. Постановка задачи
Исследование динамики примесей при поршневом вытеснении нефти водой из пористой среды приводит к краевым задачам математической физики. В общем случае разработка данной теории требует совместного рассмотрения уравнений (3.10) и (3.11) с краевыми условиями. Однако плотности в скелете ![]() и насыщающей жидкости
и насыщающей жидкости ![]() связаны равенством
связаны равенством ![]() . Это соотношение позволяет отыскивать решение только одного из уравнений, поскольку второе решение находится умножением или делением на
. Это соотношение позволяет отыскивать решение только одного из уравнений, поскольку второе решение находится умножением или делением на ![]() . Можно показать, что найденное таким образом второе решение будет удовлетворять соответствующему дифференциальному уравнению в частных производных.
. Можно показать, что найденное таким образом второе решение будет удовлетворять соответствующему дифференциальному уравнению в частных производных.
Краевые условия задачи определяются из очевидных соображений.
Требуется найти решение уравнения для жидкости
|
| (3.16) |
в виде функции ![]() , удовлетворяющие граничным условиям, в подобласти
, удовлетворяющие граничным условиям, в подобласти ![]() . Предполагается, что на левом конце стержня поддерживается постоянная концентрация радиоактивного вещества
. Предполагается, что на левом конце стержня поддерживается постоянная концентрация радиоактивного вещества ![]() , поэтому для подобласти
, поэтому для подобласти ![]() граничное условие имеет вид
граничное условие имеет вид
|
| (3.18) |
Требуется найти решение уравнения для скелета
|
| (3.17) |
в виде функции ![]() , удовлетворяющие граничным условиям, в подобласти
, удовлетворяющие граничным условиям, в подобласти ![]() .
.
В подобласти ![]() на правой подвижной границе поддерживается неизменной плотность радиоактивного вещества в скелете, поэтому граничное условие для уравнения скелета имеет вид
на правой подвижной границе поддерживается неизменной плотность радиоактивного вещества в скелете, поэтому граничное условие для уравнения скелета имеет вид
|
| (3.19) |
Это условие определяет перенос радиоактивных веществ из нефтенасыщеной зоны пористой среды в водонасыщенную.
3.1.2 Решение задач
Найдем решение уравнения (3.16) в более общем виде. То есть для уравнения
|
|
с граничным условием
|
| (3.20) |
для области ![]()
Решение уравнений (3.16) находится методом характеристик.
|
| (3.21) |
Интегрируя первое уравнение системы (16), получаем
|
| (3.22) |
Из второго уравнения следует, что ![]() , где
, где ![]() – некоторая постоянная. Но т.к.
– некоторая постоянная. Но т.к.![]() , то
, то ![]() .
.
Найдем границы области в котором есть решение.
Пусть при ![]() , тогда
, тогда
|
| |
|
| |
|
|
Для начального момента, при ![]() и
и ![]()
|
| (3.23) |
Уравнение (3.23) представляет собой границу.
Параметризуем уравнение (3.22).
Зададим ![]() так, чтобы получить значение при
так, чтобы получить значение при ![]() , т. е.
, т. е. ![]() .
.
При ![]() ,
, ![]()
|
| (3.24) |
|
| (3.25) |
Подставляя значение параметра в (15) получим
|
| (3.26) |
Так как ![]() , то
, то
|
| (3.27) |
Таким образом это выражение (3.27) есть решение уравнения (3.16) в более общем виде.
Для частного случая, т. е. ![]() не зависит от
не зависит от ![]() , решение
, решение
|
| (3.28) |
Полученное решение (8) для плотности радиоактивного вещества в вытесняющей жидкости, удовлетворяет граничному условию для жидкости в подобласти ![]() .
.
Решение для плотности радиоактивного вещества в скелете в той же области получим из условия равенства химических потенциалов
| | (3.29) |
Таким же образом, в более общем виде решим уравнение для скелета
|
| (3.30) |
с граничным условием
|
| (3.31) |
для области ![]() .
.
|
| (3.32) |
Интегрируя первое уравнение (3.32), получаем
|
| (3.33) |
Из второго уравнения следует, что ![]() , где
, где ![]() – некоторая постоянная. Но т.к.
– некоторая постоянная. Но т.к.![]() , то
, то ![]() .
.
Параметризуем уравнение (3.33): при ![]() ,
, ![]() . Тогда
. Тогда
|
|
|
|
Так как
|
|
|
|
|
| (3.34) |
Подставим значение параметра (3.34) в граничное условие для скелета пористой среды
|
|
То теперь
|
| (3.35) |
Выражение (3.35) есть решение уравнения для скелета (3.30) в общем виде. Частное решение получаем из (3.35) исключая ![]() .
.
|
| (3.36) |
Полученное решение (3.36) для плотности радиоактивного вещества в скелете, удовлетворяет граничному условию подобласти ![]() .
.
Используя соотношение (3.15) находим решение для плотности радиоактивного вещества в вытесняющей жидкости подобласти ![]() получим из условия равенства химических потенциалов
получим из условия равенства химических потенциалов
| | (3.37) |
Проверка значений на границах подобласти
При ![]() ,
, ![]() на правой границе
на правой границе
|
| (3.38) |
при ![]() и
и ![]() на левой границе
на левой границе
|
| (3.39) |
Окончательное выражение для плотности радиоактивного вещества в вытесняющей жидкости имеет вид:
|
| (3.40) |
и для плотности радиоактивного вещества в скелете в той же области получим
|
| (3.41) |
Для области ![]() , занимаемой вытесняемой нефтью плотности радиоактивного вещества в скелете и нефти остаются неизменными:
, занимаемой вытесняемой нефтью плотности радиоактивного вещества в скелете и нефти остаются неизменными:
|
| (3.42) |
Результирующая плотность радиоактивных веществ в пористой среде ρ+ складывается из плотности в насыщающей жидкости, скелете и нефти, поэтому окончательное выражение имеет вид
|
| (3.43) |
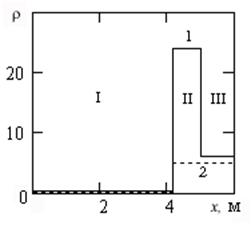
На рисунке приведена зависимость относительной плотности радиоактивного вещества ![]() от координаты
от координаты ![]() в фиксированный момент времени. В расчетах принято:
в фиксированный момент времени. В расчетах принято: ![]() =0.2, μ΄/μs΄=0.05, μo΄/μw΄=10, ρs0/ρw0=5. Сплошной линией изображен график зависимости относительной результирующей плотности радиоактивных веществ, а пунктирной ‑ их плотность в скелете.
=0.2, μ΄/μs΄=0.05, μo΄/μw΄=10, ρs0/ρw0=5. Сплошной линией изображен график зависимости относительной результирующей плотности радиоактивных веществ, а пунктирной ‑ их плотность в скелете.
Из рисунка видно, что в области ![]() образуется зона II с повышенным содержанием радиоактивных веществ. Отметим, что на границах зон наблюдается скачкообразное изменение плотности радиоактивного вещества. В реальных условиях эти скачки нивелируются диффузией, которая в рассматриваемом случае для простоты не учитывается.
образуется зона II с повышенным содержанием радиоактивных веществ. Отметим, что на границах зон наблюдается скачкообразное изменение плотности радиоактивного вещества. В реальных условиях эти скачки нивелируются диффузией, которая в рассматриваемом случае для простоты не учитывается.
|
|
| Рис.5. Зависимость относительной плотности радиоактивного вещества в пористой среде от пространственной координаты в фиксированный момент времени: I – промытая зона, II – зона радиогеохимического эффекта; III – нефтенасыщенная зона; 1 – результирующие значения плотности в пористой среде, 2 – составляющая плотности в скелете |
Из анализа кривых, приведенных на рисунке, следует, что возникновение зоны с повышенной радиоактивностью объясняется вымыванием радиоактивных веществ, первоначально сосредоточенных в скелете, водой.
Из изложенного выше следует, что область радиогеохимического эффекта представляет зону обратного массового влияния вытесняемой жидкости на вытесняющую. Это происходит за счет взаимодействия жидкостей через скелет. Дело состоит в том, что скорость движения границы вытеснения ![]() превышает скорость конвективного переноса примесей в пористой среде
превышает скорость конвективного переноса примесей в пористой среде ![]() , с которой только и возможно движение разрывов. В результате размеры области радиогеохимического эффекта увеличиваются со временем со скоростью
, с которой только и возможно движение разрывов. В результате размеры области радиогеохимического эффекта увеличиваются со временем со скоростью ![]() , которая, как показывают оценки, в несколько раз превышает скорость
, которая, как показывают оценки, в несколько раз превышает скорость ![]() . Процессы, аналогичные описываемым, происходят при формировании черенковского излучения.
. Процессы, аналогичные описываемым, происходят при формировании черенковского излучения.
В реальных условиях возможность измерения распределения радиоактивности в пласте ограничена только определенным числом скважин, в области расположения которых происходит обводнение пласта. В этих скважинах возможно измерение зависимости радиоактивности от времени. Отметим, что наблюдаемая при этом временна̀я развертка радиоактивности соответствует пространственной, изображенной на рисунке.
3.3.2 Условие возникновения радиогеохимического эффектаУсловие возникновения радиогеохимического эффекта заключается в повышении радиоактивного фона, математическим выражением которого является неравенство ![]() , откуда с использованием (20) получим
, откуда с использованием (20) получим
|
| (3.44) |
После соответствующих преобразований получим
|
| (3.45) |
Неравенство (3.45) определяет соотношение производных химического потенциала, при котором наблюдается радиогеохимический эффект. В условие (3.45) не входит пористость, это означает, что радиогеохимический эффект должен наблюдаться в пластах с любой пористостью. Отметим, однако, что величина эффекта согласно предлагаемой теории пропорциональна пористости
|
| (3.46) |
где ![]() – коэффициент, зависящий от выбора единиц измерения.
– коэффициент, зависящий от выбора единиц измерения.
Заключение
Таким образом, предложенная теория в достаточной мере отражает механизм перекачки радиоактивных веществ и образование зоны радиогеохимического эффекта. Полученные результаты могут быть использованы при интерпретации результатов геолого-промысловых исследований для определения принимающих и отдающих интервалов пластов. Они позволяют также более глубоко понять процессы, происходящие с растворенными веществами при движении пресных питьевых вод в подземных пластах.
Литература
1. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. – М.: Наука. – 1986. – 773 с.
2. Орлинский Б.М. Котроль за разработкой нефтяных месторождений. – М.:Недра, 1982.
3. Хуснуллин М.Х. Геофизические методы контроля разработки нефтяных пластов. –М: Недра, 1989.
4. Валиуллин Р.А., Шарафутдинов Р.Ф., Азизов Ф.Ф., Никифоров А.А., Зелеев М.Х. Исследование закономерностей формирования радиогеохимического эффекта в пласте//Изв. ВУЗов. Нефть и газ. №3, 2000. С 26-31.
5. Советский энциклопедический словарь. – М.: «Советская энциклопедия», 1985. Под ред. Прохорова А.М.
Похожие работы
... самого предприятия так как слишком статична и может привести к некоторой неадекватности решений при оперативном их принятии. 2. Экологическая оценка современного состояния гурзуфского парка-памятника садово-паркового искусства Современное экологическое состояние парка можно охарактеризовать как хорошее, но требующее срочных мер по предотвращению воздействия негативных факторов на ...
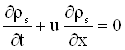 ,
,

 .
.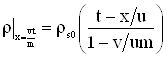 ,
,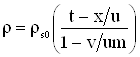 ,
,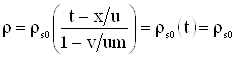 ;
;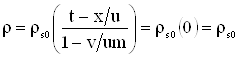 .
.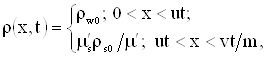
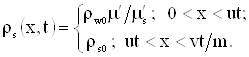
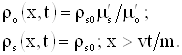

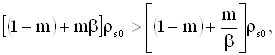
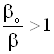 .
. ,
,


0 комментариев