Фазовые переходы в ферромагнетиках

2. Фазовые переходы в ферромагнетиках

Ферромагнетики - удивительно простые системы, в которых наблюдаются фазовые переходы различных типов.

Рассмотрим решетку, в узлах которой расположены взаимодействующие между собой спины si (магнитные моменты). Энергия взаимодействия пары спинов (обычно учитывается взаимодействие только ближайших соседей).

Eij = -J (si sj) .

Полная энергия E и намагниченность M данной конфигурации спинов {s1, s2, ... sn} могут быть найдены суммированием по всей решетке. В модели Гейзенберга каждый спин может принимать произвольное направление. Если спин вращается в плоскости - это XY модель.

В модели Изинга каждый спин может принимать только два выделенных направления si = +-1 (вверх или вниз). Поскольку si может принимать 2 значения, у системы из n спинов есть 2n различных конфигураций. Ниже приведены 24 = 16 возможных конфигураций спинов и соответствующие энергии для решетки 2x2

E = -4J E = 4J

+ + - - + - - +

+ + - - - + + -

E = 0

- + + - + + + ++ - - + - - - -- - + - + + - +

+ + + + + - - +- - - - - + + -+ + + - - - - +

Для ферромагнетика константа обменного взаимодействия J > 0 и энергия минимальна для спинов, направленных в одну сторону. Система вырождена, т.к. одной энергии соответствует несколько различных конфигураций спинов. Энтропия системы S(E) растет с увеличением степени вырождения состояний с энергией E. Энтропия минимальна в упорядоченном состоянии (при минимальной энергии) и быстро растет с ростом энергии.

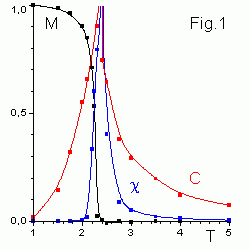рис. 2

Предполагается, что спины взаимодействует также с термостатом с температурой T. В термодинамическом равновесии система стремится к минимуму F = E - T S. Поэтому при низкой температуре она переходит в состояние с минимальной энергией (все спины направлены в одну сторону). Т.о. взаимодействие спинов приводит к их упорядочиванию и появлению макроскопической намагниченности M (см. рис.2). При высокой температуре системе выгоднее уменьшить F за счет увеличения ее энтропии (беспорядка). Тепловые флуктуации разрушают упорядочивание и намагниченность системы обращается в ноль.

В двумерном модели Изинга при критической температуре Tc = 2.269 происходит фазовый переход из неупорядоченного в упорядоченное ферромагнитное состояние.

 

3. Распределение Гиббса

В состоянии термодинамического равновесия вероятность конфигурации спинов системы {s1, s2, ... sn} определяется функцией распределения Гиббса

w(s1, ... sn) = 1/Z exp[ -E(s1, ... sn)/T ],(1)

где Z - нормировочный коэффициент, называемый статистической суммой и определяемый из условия

∑ s1 ∑ s2 ... ∑ sn w(s1,...sn) = 1, Z = ∑ s1 ∑ s2 ... ∑ sn exp[ -E(s1,...sn)/T ].

Тогда, например, усредненная по функции распределения Гиббса энергия системы

<E>G = ∑ s1 ∑ s2 ... ∑ sn E(s1, ... sn) w(s1, ... sn) =

1/Z ∑ s1 ∑ s2 ... ∑sn E(s1, ... sn) exp[ -E(s1, ... sn)/T] .

В 1944г. Л.Онзагер нашел точное решение для двумерной модели Изинга. В принципе, среднее для любого конечного n может быть найдено перебором всех спиновых конфигураций, но для макроскопических систем (например при n = 100) это невозможно для любой ЭВМ. Однако вклад различных слагаемых в сумму не равнозначен. Из (1) следует, что вероятность нахождения в состоянии с энергией E

w(E) ~ n(E) exp(-E/T),

где n(E) - число конфигураций с энергией E. Последнее выражение можно переписать

w(E) ~ exp[S(E)-E/T],

где S(E) = ln n(E) - энтропия состояний с данной энергией. Поэтому в равновесии среди всех состояний системы чаще будут встречаться конфигурации, для которых велики w(E) и S(E)-E/T.

4. Модель Изинга

 

Модель Изинга --- математическая модель статистической физики, предназначенная для описания намагничивания материала.

Каждой вершине кристаллической решётки (рассматриваются не только трёхмерные, но и одно- и двумерные случаи) сопоставляется число, называемое "спином " и равное +1 или -1 ("поле вверх"/"поле вниз"). Каждому из 2^N возможных вариантов расположения спинов (где N --- число атомов решётки) приписывается энергия, получающаяся из попарного взаимодействия спинов соседних атомов:

где J --- энергия взаимодействия (в простейшем случае одна и та же для всех пар соседних атомов). Иногда также рассматривается внешнее поле h (часто полагаемое малым):

Затем, для заданной обратной температуры eta=1/k_B T на получившихся конфигурациях рассматривается распределение Больцмана: вероятность конфигурации полагается пропорциональной e^{-eta E(S)} , , и исследуется поведение такого распределения при очень большом числе атомов N.

Например, в моделях с размерностью, большей 1, имеет место фазовый переход: при достаточно низких температурах большая часть спинов ферромагнетика (J>0) будет ориентирована (с близкой к 1 вероятностью) одинаково, а при высоких почти наверняка спинов "вверх" и "вниз" будет почти поровну. Температура, при которой происходит этот переход (иными словами, при которой исчезают магнитные свойства материала), называется критической, или точкой Кюри.

В этой модели предполагается, что атомы располагаются неподвижно, не совершая колебаний, в узлах идеальной кристаллической решетки. Расстояния между узлами решетки постоянно, оно не зависит ни от температуры, ни от намагниченности, то есть в этой модели не учитывается теплового расширения твердого тела.

Взаимодействие между магнитными моментами в модели Изинга учитывается, как правило, лишь между ближайшими соседями. Считается, что величина этого взаимодействия также не зависит от температуры и намагниченности. Взаимодействие обычно (но не всегда) считается центральным и парным.

Однако даже в такой простой модели изучение фазового перехода ферромагнетик–парамагнетик встречает огромные математические трудности. Достаточно сказать, что точного решения трехмерной задачи Изинга в общем случае до сих пор не получено, а применение более-менее точных приближений в этой задаче приводит к большим вычислительным трудностям и находится на грани возможностей даже современной вычислительной техники.

5. Линейная модель Изинга с дальним взаимодействием

Двумерная модель Изинга с дальним взаимодействием до сих пор не решена. Поэтому представляет интерес рассмотрение поведения упрощенных моделей с дальним взаимодействием. Одной из таких моделей является линейная (одномерная) модель со взаимодействием ближайших и следующих за ближайшими соседей.

Для описания взаимодействия в такой модели введем матрицу с тремя индексами Wijl с элементами:

< i|W|j>|l>=exp(θ1σiσj)exp(θ2σiσj), θ1 =J1 /kT, θ2 =J2/kT, (1)

где J1 иJ2 -параметры взаимодействия ближайших и следующих за ближайшими соседей соответственно, k –постоянная Больцмана, Т –абсолютная температура, конфигурационные переменные σi ,σj ,σl независимо принимают значения ±1.

В стандартных обозначениях для многомерных матриц элементы матрицы (1) можно расположить в виде прямоугольной таблицы:

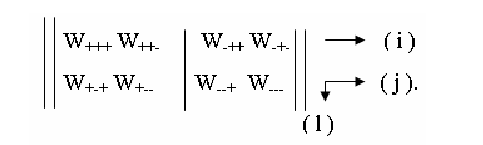
Стрелки указывают направление, в котором возрастают соотвецтвующие индексы. В качестве значений индексов мы выбрали значения конфигурационных переменных σi,σj,σl ,причем в двоичной системе счисления знаку плюс сопоставляем 0, знаку минус сопоставляем 1.