Навигация
1.1 Скорость света
Мировая линия фотона, называемая нулевой геодезической, определяется так, что![]() всегда равно нулю. Уравнение (1.1.5) показывает, что на нулевой геодезической в бесконечном удалении от начала
всегда равно нулю. Уравнение (1.1.5) показывает, что на нулевой геодезической в бесконечном удалении от начала
![]()
т. е. координатная скорость света в «пустом» пространстве равна ![]() , Однако в нашем евклидовом пространстве координатная скорость света не равна
, Однако в нашем евклидовом пространстве координатная скорость света не равна![]() . Приняв в
. Приняв в![]() имеем
имеем
![]() (1.1.6)
(1.1.6)
что эквивалентно
![]() (1.1.7)
(1.1.7)
Скорость света в произвольной точке х зависит от радиальной координаты и направления. В радиальном направлении скорость задается формулой
![]()
в то время как в тангенциальном направлении
![]()
и, следовательно,
![]()
1.2 Шварцшильдовы координаты
Рассмотрим преобразование пространственных координат
![]()
где![]() всегда равно
всегда равно![]() .
.
Дифференцируя это выражение и учитывая, что![]() получаем
получаем
![]()
откуда следует, что
![]()
и
![]()
Из формул![]() видно, что выражение (1.1.2) для интервала
видно, что выражение (1.1.2) для интервала![]() преобразуется к виду
преобразуется к виду
![]()
Где
![]()
Выражение ![]() — векторная форма метрики в стандартных координатах Шварцшильда; соответствующую скалярную форму в сферических координатах, как строгое решение уравнений Эйнштейна, впервые получил в 1916 г. К. Шварцшильд.
— векторная форма метрики в стандартных координатах Шварцшильда; соответствующую скалярную форму в сферических координатах, как строгое решение уравнений Эйнштейна, впервые получил в 1916 г. К. Шварцшильд.
Мы показали, что общее выражение (1.1.2) с помощью формул (1.1.3) и (1.1.4) может быть приведено к шварцшильдовой форме (1.1.12) путем чисто алгебраического преобразования соотношения (1.1.8). Таким образом, уравнения, выведенные с использованием метрики Шварцшильда, можно преобразовать к некоторой общей сферически симметричной метрике.
1.3 Изотропные координаты
Рассмотрим систему координат, определяемую формулой
![]()
В соответствии с (1.1.3), получаем
![]()
Дифференцируя (1.1.14) по![]() , находим
, находим
![]()
Следовательно, по (1.1.4) имеем
![]()
или
![]()
и выражение (1.1.2) для элемента![]() принимает вид
принимает вид
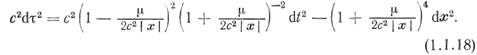
Это выражение известно как изотропная форма метрики Шварцшильда, поскольку, приняв в![]() , можно найти, что координатная
, можно найти, что координатная
скорость света в точке х, задаваемая формулой
![]()
одинакова во всех направлениях.
2. УРАВНЕНИЯ ГЕОДЕЗИЧЕСКИХ
Можно показать (см. Приложение В), что уравнения, определяющие геодезические, выводятся из обычных уравнений Эйлера — Лагранжа, которые в координатах Шварцшильда имеют вид
![]()
![]()
где![]() — лагранжиан,
— лагранжиан,
![]()
а точка сверху обозначает дифференцирование по![]()
Уравнение (1.2.1) дает непосредственно
![]()
Или
![]()
где![]() — постоянная интегрирования.
— постоянная интегрирования.
Формула (1.2.2) приводит к следующему выражению, вывод которого содержится в Приложении В:
![]()
Умножая (1.2.2) векторно на![]() , получаем
, получаем
![]()
вследствие того что![]() Таким образом,
Таким образом,
![]()
где Н — постоянная, а h — постоянный единичный вектор. Из последнего уравнения следует, что геодезическая лежит в плоскости, перпендикулярной h, а угловой момент по отношению к собственному времени остается неизменным. Угловой момент постоянен только в координатах Шварцшильда. В произвольной метрике, для которой ![]() уравнение (1.2.6) имеет вид
уравнение (1.2.6) имеет вид
![]()
правая часть которого не является постоянной, поскольку x — функция![]()
При этих условиях (1.2.6) эквивалентно уравнению
![]()
и, следовательно, уравнение геодезической (1.2.5) в координатах Шварцшильда принимает вид
![]()
Похожие работы
... интерпретации, в СТО нет ничего, кроме описания пространственно-временных свойств безмассовых полей в различных ИСО. Этот вывод, примененный к общей теории относительности, не затрагивая математической структуры ОТО, кардинальным образом изменяет ее интерпретацию, позволяя переосмыслить традиционный геометрический подход в теории гравитации ( [2], c. 28-39). 3. К ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ В ...
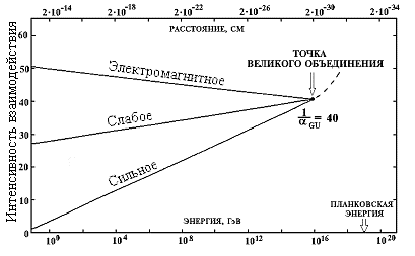
... представляют собой проявление одного и того же фундаментального принципа. Эйнштейн опередил свое время. В то время, когда он жил, еще не было известно сильное и слабое взаимодействие, поэтому он так и не смог выстроить Единую Теорию Поля. Больше того, его поиски в то время были мало понятны большинству физиков - почти все из них были озабочены разработкой новой дисциплины - квантовой механикой. ...
... Вселенной. 5. Проблемы ОТО 5.1 Проблема энергии Так как энергия, с точки зрения математической физики, представляет собой величину, сохраняющуюся из-за однородности времени[53], а в общей теории относительности, в отличие от специальной, вообще говоря, время неоднородно[~ 4], то закон сохранения энергии может быть выражен в ОТО только локально, то есть в ОТО не существует такой ...
... о биологической причинности. Ряд феноменов, которые витализм считал специфическими для биологических объектов (способность к саморегуляции, усложнение строения, достижение одного результата разными способами) рассматриваются в современном естествознании как типичные проявления процессов самоорганизации любых достаточно сложных систем, а не только живых. Н.Бор: “ни один результат биологического ...


0 комментариев