Навигация
7.2. ВЗВЕДЕНИЕ УДАРНИКА
При движении затворной рамы 1 (рисунок 7.2) в крайнее заднее положение она воздействует на ударник 5 взводя его при этом в месте контакта возникают сила ![]() и сила трения
и сила трения ![]() . При движении затворной рамы по внутренней поверхности затвора возникают сила
. При движении затворной рамы по внутренней поверхности затвора возникают сила ![]() и сила трения
и сила трения ![]() , а при взведении ударника возникает сила
, а при взведении ударника возникает сила ![]() и сила трения
и сила трения ![]() . Ударник на затворную раму действует с силами, равными соответственно
. Ударник на затворную раму действует с силами, равными соответственно ![]() и
и ![]() , направленными в противоположную сторону.
, направленными в противоположную сторону.
Приложим к основному звену потерянную силу ![]() , и к ударнику -
, и к ударнику - ![]() и запишем следующие зависимости, проектируя силы на направление движения основного звена 1:
и запишем следующие зависимости, проектируя силы на направление движения основного звена 1:
Для ударника:
![]() (7.2.1)
(7.2.1)
![]() (7.2.2)
(7.2.2)
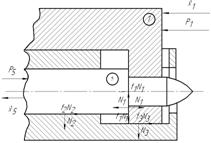
Рисунок 7.2. Взведение ударника.
Из уравнения (7.2.1) определяем ![]() :
:
![]() (7.2.3)
(7.2.3)
Для затворной рамы:
![]() (7.2.4)
(7.2.4)
![]() (7.2.5)
(7.2.5)
Из уравнения (7.2.4) определяем ![]()
![]() :
:
![]() (7.2.6)
(7.2.6)
Из уравнения (7.2.5) определяем ![]() и подставляем в уравнение (7.2.6):
и подставляем в уравнение (7.2.6):
![]() (7.2.7)
(7.2.7)
Поделив уравнения (7.2.7) на (7.2.3) получим:
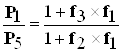 (7.2.8)
(7.2.8)
Так как
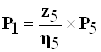 ,
,
то
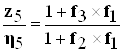 (7.2.9)
(7.2.9)
Зная выражение для коэффициента передачи сил, легко найти значение передаточного отношения. Коэффициент передачи сил равен передаточному отношению, если связи идеальны. Тогда при ![]()
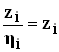 . (7.2.10)
. (7.2.10)
Для нашего механизма при ![]()
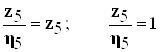 (7.2.11)
(7.2.11)
Учитывая, что ![]() определяем коэффициент приведения масс:
определяем коэффициент приведения масс:
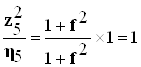 (7.2.12)
(7.2.12)
7.3. ВЗВЕДЕНИЕ ЗАДЕРЖКИ УДАРНИКА
При движении ударника 1 (рисунок 7.3) в крайнее заднее положение он воздействует на задержку ударника 8 взводя его при этом в месте контакта возникают сила ![]() и сила трения
и сила трения ![]() . При движении ударника по внутренней поверхности затвора возникают сила
. При движении ударника по внутренней поверхности затвора возникают сила ![]() и сила трения
и сила трения ![]() .
.
Приложим к основному звену потерянную силу ![]() , и к задержке ударника -
, и к задержке ударника - ![]() и запишем следующие зависимости, проектируя силы на оси
и запишем следующие зависимости, проектируя силы на оси ![]() и
и ![]() :
:
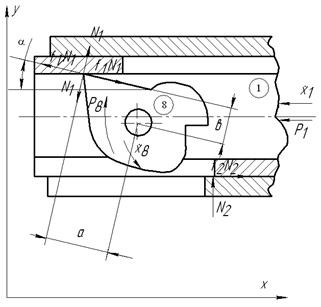
Рисунок 7.3. Взведение задержки.
Для ударника:
![]() (7.3.1)
(7.3.1)
![]() (7.3.2)
(7.3.2)
Из уравнения (7.3.2) определяем ![]() :
:
![]() (7.3.3)
(7.3.3)
Подставляем полученное выражение (7.3.3) в уравнение (7.3.1):
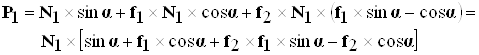 (7.3.4)
(7.3.4)
Для предохранителя ударника:
![]() (7.3.5)
(7.3.5)
Определяем из уравнения (7.3.5) ![]() :
:
![]() (7.3.6)
(7.3.6)
Поделив уравнения (7.3.6) на (7.3.3) получим:
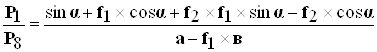 (7.3.7)
(7.3.7)
Так как
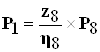 , то
, то
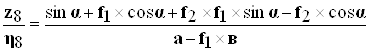 (7.3.8)
(7.3.8)
Зная выражение для коэффициента передачи сил, легко найти значение передаточного отношения. Коэффициент передачи сил равен передаточному отношению, если связи идеальны. Тогда при ![]()
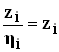 . (7.3.9)
. (7.3.9)
Для нашего механизма при ![]()
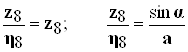 (7.3.10)
(7.3.10)
Учитывая, что ![]() определяем коэффициент приведения масс:
определяем коэффициент приведения масс:
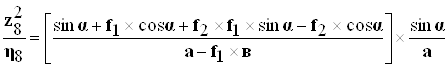 (7.3.11
(7.3.11
0 комментариев