Построение эконометрической модели и исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка

Министерство образования Республики Беларусь

Белорусский Государственный Университет

Экономический факультет

Кафедра Экономической и институциональной экономики

Курсовой проект

По дисциплине «Эконометрика и прогнозирование»

На тему

«Построение эконометрической модели и исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка»

Выполнила

Студентка третьего курса

Отделения «Экономическая теория»

Волкова Ольга Александровна

Научный руководитель:

Абакумова Юлия Георгиевна

Минск, 2008 г.

Содержание

Введение

Теоретический раздел

Аналитический раздел

Построение базовой регрессионной модели и оценка её качества

Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка

Устранение гетероскедастичности в модели

Заключение

Список использованных источников

Введение

Вся история развития человечества неразрывно связана с изменениями динамики численности и воспроизводства населения. Современные очень высокие темпы роста численности населения мира в решающей степени определяются темпами его увеличения в развивающихся странах.

Современный «взрыв» населения в развивающихся странах имеет существенные особенности. Главная особенность заключается в том, что если в Европе быстрый рост населения был обусловлен в первую очередь социально-экономическими изменениями, т.е. следовал за экономическим ростом и изменениями в социальной сфере, то в развивающихся странах мы наблюдаем прямо противоположную картину: быстрый рост населения значительно опережает их экономическое и социальное развитие, усугубляя тем самым и без того ложные проблемы занятости, социальной сферы, обеспечения продовольствием, экологии.

Наряду с наблюдаемым во второй половине XX века демографическим взрывом проявился и демографический кризис, затронувший в первую очередь развитые страны мира.

Суть современного демографического кризиса заключается не только в резком ухудшении развития народонаселения, что выражается в резком уменьшении темпов роста численности населения в развитых странах, а в некоторых из них и снижении этого показателя за нулевую отметку, но и в определенном кризисе института семьи, в некотором ухудшении качества развития населения, в демографическом старении.

Наблюдаемая в развитых странах мира тенденция к резкому падению рождаемости значительно ниже уровня, обеспечивающего простое воспроизводств населения, ведет к значительному демографическому старению, сокращению трудовых ресурсов и увеличению «экономической нагрузки» на экономически активное население, на старение населения или увеличение доли пожилых и старых людей.

Итак, изменение показателя общей численности населения происходит под воздействием целого ряда прямых и косвенных факторов. В своей работе я бы хотела рассмотреть влияние показателей рождаемости, смертности и численности пожилого населения в разных странах мира на общую численность населения этих стран.

Такой выбор обусловлен, в первую очередь, целью моей работы – проверка регрессионной модели на гетероскедастичность (т.к. эта проблема в большей степени присуща пространственным данным и редко встречается во временных рядах).

Таким образом построенная мною модедь содержит следующие объясняющие переменные:

X₁ – численность рожденных детей за 2007г. (чел.),

X₂ – численность умерших за 2007г. (чел),

Х₃ – численность населения в возрасте от 65 лет и старше (чел.), и объясняемую переменную:

Y – общая численность населения на начало 2008г. (чел.).

Статистические данные по странам взяты за период 2007г, влияющие на общую численность населения начала 2008г. (Таблица 1)

Страны	Общая численность населения на начало года	X1- численность рожненных детей за 2007г.	X2 - смертность за 2007г.	X3 - численность населения старше 65 лет за 2007г.
Бельгия	10666866	120663	374.0553	1824034.086
Болгария	7640238	75349	693.2108	1321761.174
Чехия	10381130	114632	355.3592	1484501.59
Дания	5475791	64082	256.328	837796.023
Германия	82221808	682700	2594.26	16279917.98
Эстония	1340935	15775	78.875	229299.885
Ирландия	4419859	70623	261.3051	490604.349
Греция	11214992	110048	418.1824	2085988.512
Испания	45283259	488335	1806.8395	7562304.253
Франция	63753140	816500	3102.7	10328008.68
Италия	59618114	563236	2140.2968	11864004.69
Кипр	794580	8529	52.8798	97733.34
Латвия	2270894	23273	202.4751	388322.874
Литва	3366357	32346	190.8414	525151.692
Люксембург	483799	5477	9.8586	67731.86
Венгрия	10045000	97600	575.84	1597155
Мальта	410584	3871	25.1615	56660.592
Нидерланды	16404282	180882	741.6162	2378620.89
Австрия	8331930	76250	282.125	1408096.17
Польша	38115641	387873	2327.238	5107495.894
Португалия	10617575	102492	348.4728	1836840.475
Румыния	21528627	214728	2576.736	3207765.423
Словения	2025866	19636	60.8716	322112.694
Словакия	5400998	54424	331.9864	642718.762
Финляндия	5300484	58729	158.5683	874579.86
Швеция	9182927	103421	258.5525	1597829.298
Великобритания	61185981	770651	3467.9295	9789756.96
Турция	70586256	1361000	29533.7	4658692.896
Исландия	314321	4508	6.3112	36775.557
Норвегия	4737171	58459	181.2229	691626.966
Швейцария	7591414	74440	290.316	1229809.068

Табл. 1

Теоретический раздел

При практическом проведении регрессионного анализ модели с помощью МНК необходимо обращать внимание на проблемы, связанные с выполнимостью свойств случайных отклонений модели, т.к. свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса-Маркова), т.к. при их нарушении МНК может давать оценки с плохими статистическими свойствами.

Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений: т.е. D( ε_i ) = D( ε_j ) = σ² для любых наблюдений i и j. Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).

Наличие гетероскедастичности может привести к снижению эффективности оценок, полученных по МНК, к смещению дисперсий, к ненадежности интервальных оценок, получаемых на основе соответствующих t- и F-статистик. Таким образом, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключения по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно можно признать статистически значимыми коэффициенты, которые таковыми не являются. Причиной гетероскедастичности могут быть выбросы (резко выделяющиеся наблюдения), ошибки спецификации модели, ошибки в преобразовании данных, ассиметрия распределения какой-либо из объясняющих переменных. Чаще всего, появление проблемы гетероскедастичности можно предвидеть и попытаться устранить этот недостаток еще на этапе спецификации. Однако обычно приходиться решать эту проблему уже после построения уравнения регрессии. Не существует какого-либо однозначного метода определения гетероскедастичности. Существует довольно большое количество тестов и критериев, наиболее популярными и наглядными из которых являются: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфельда-Квандта и тест Уайта. Моя работа посвящена исследованию поледних двух тестов.

Тест Уайта

Алгоритм этого теста заключается в том, что сперва оценивается исходная модель и определяются остатки ε_i , затем строится вспомогательно уравнение регрессии и определяется его коэффициент детерминации, произведение n*R^2 сравнивается со значением χ^2- распределения и делается вывод о наличии или об отсутствии гетероскедастичности.

Тест Парка

Парк в свою очередь предложил следующую функциональную зависимость:

Алгоритм теста:

1) Оцениваем исходное уравнение и определяем e_i.

2) Оцениваем уравнение

Проверяем статистическую значимость коэффициента β уравнения на основе статистики

Если β значим, то гетероскедастичность. Если нет, то гомоскедастичность.

Тест Бреуша-Пагана-Годфри

1)  Оценивается исходная модель и определяются остатки

Строится оценка:

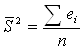
2)  Оценивается регрессия

 

Если

При установлении присутствия гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Сначала можно попробовать устранить возможную причину гетероскедастичности, скорректировав исходные данные, затем попробовать изменить спецификацию модели, а в случае, если не помогут эти меры, использовать метод взвешенных наименьших квадратов.

Далее в работе проведем довольно полный анализ базовой модели, включая непосредственно тесты на обнаружение гетероскедастичности.

Аналитический раздел