Построение базовой регрессионной модели и оценка её качества

1. Построение базовой регрессионной модели и оценка её качества

По данным Таблицы 1 построим исходную модель с помощью пакета Eviews3.1. Получим следующее уравнение построенной модели:

Где:

Population – общая численность населения на начало 2008г. (чел.),

Birth – численность рожденных детей за 2007г. (чел.),

Mortality – численность умерших за 2007г. (чел),

Old – численность населения в возрасте от 65 лет и старше (чел.).

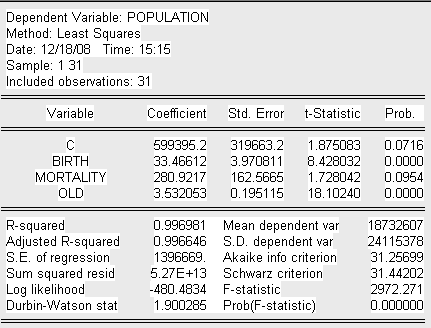
Проверим на значимость коэффициенты уравнения регрессии. Для этого оценим t-статистику:

Используем в данном случае уровень значимости . Тогда критическое значение t-статистики соответственно:

Значения t-статистик рассматриваемых переменных больше критического значения (критерий Стьюдента), следовательно делаем вывод о их значимости. По анализу исследованных t-статистик и коэффициента детерминации R-квадрат делаем предварительный вывод об адекватности построенной модели.

Продолжая оценивать общее качество модели, используем критерий Фишера:

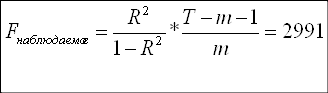
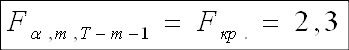
Н0: R-квадрат=0

Н1: R-квадрат>0

Так как F-наблюдаемое больше F-критического, принимаем гипотезу Н1, согласно которой модель адекватна. Поскольку значение F-наблюдаемого велико, можно сделать предположение о наличии мультиколлинеарности, что будет проверено мною в дальнейшем.

Оценим также распределение остатков в модели:

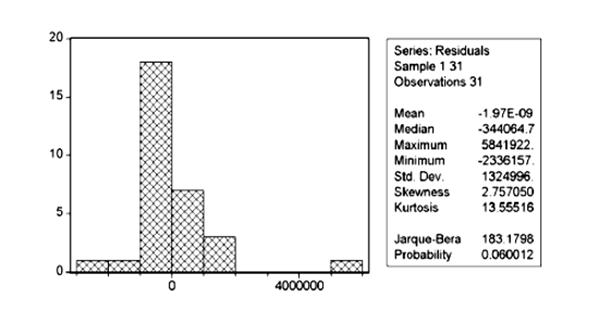
P (J-B) = 0,06, следовательно присутствует нормальное распределение остатков.

Проверим модель на присутствие автокорреляции. Для этого будем использовать тесты Бреуша-Годфри и Дарбина-Уотсона.

1) Первоначально воспользуемся тестом Бреуша-Годфри и оценим модель на присутствие автокорреляции по трем лагам:

Запишем значение  распределения для последующего сравнения с Obs* R-squared:

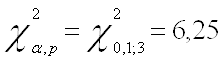
Приведем результаты теста с lag = 1:

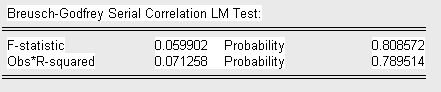
с lag = 2:

с lag = 3:

Сделаем выводы об отсутствии серийной корреляции, так как во всех трех случаях Obs* R-squared меньше

а P-вероятность статистики Бреуша-Годфри больше уровня значимости

()

2) Воспользуемся также тестом Дарбина-Уотсона:

Приведем значение статистики:

Значения критических точек

при уровне значимости :

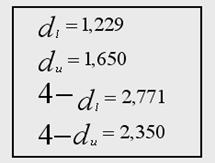
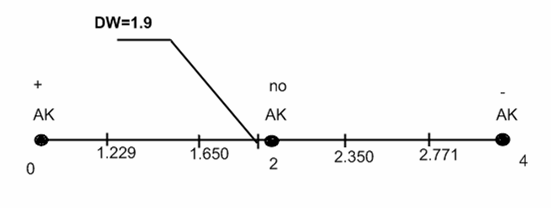
Делаем вывод об отсутствии автокорреляции, т.к. значение статистики D-W в данном случае близко к 2.

Выполним проверку регрессионной модели на мультиколлинеарность.

Построим корреляционную матрицу коэффициентов:

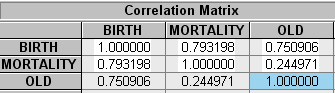
Найдем частные коэффициенты корреляции:

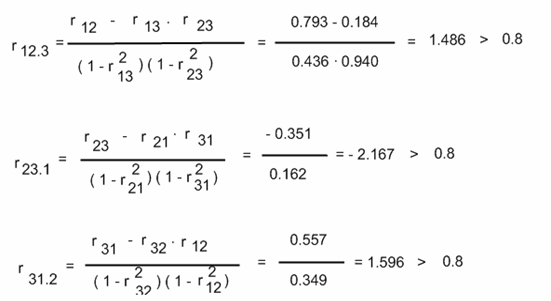
Делаем вывод о наличии высокой зависимости (коллинеарности) между переменными в каждом из трех случаев. Следовательно в модели присутствует мультиколлинеарность. Эта проблема оказывает определенное влияние на качество модели, однако ее устранение не является обязательным этапом, поэтому перейдем к дальнейшему исследованию качества регрессионной модели.

2. Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка

Переходим непосредственно к основной теме курсвой - проверяем модель на наличие гетероскедастичности. Для этого первоначально проведем тест Вайта и оценим его результаты:

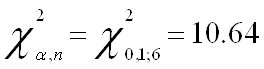
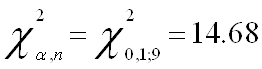
Т.к. значение P- вероятности в обоих случаях теста Уайта (no cross terms/ cross terms) меньше уровня значимости

() и Obs*

R-squared превышает

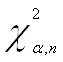
то принимаем гипотезу о наличии гетероскедастичности в модели.

Дополнительно можно использовать графический анализ ряда остатков, который подтверждает вывод о наличии гетероскедастичности, т.к. график имеет выбросы и не укладывается в полосу постоянной ширины, параллельную оси ОХ (-1000000,1000000).

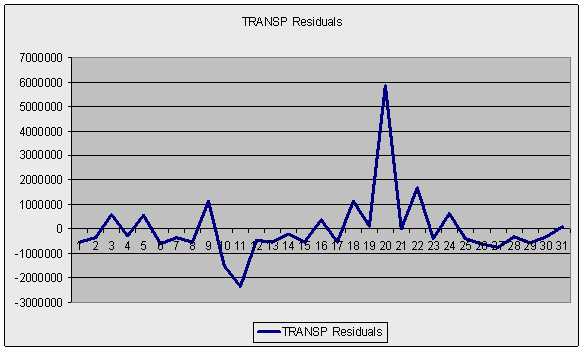
Таким образом, в этой модели мы имеем две проблемы – мультиколлинеарность и гетероскедастичность, в связи с чем нельзя доверять статистическим выводам и оценкам качества регрессионной модели. Продолжим дальнейший анализ модели с помощью теста Парка. Данный тест не предполагает особой свободы выбора и мы строим три регрессионные модели натуральных логарифмов остатков базовой модели на натуральные логарифмы каждой объясняющей переменной отдельно.

Представим вспомогательную модель 1 теста Парка:

Запишем уравнение вспомогательной модели 1:

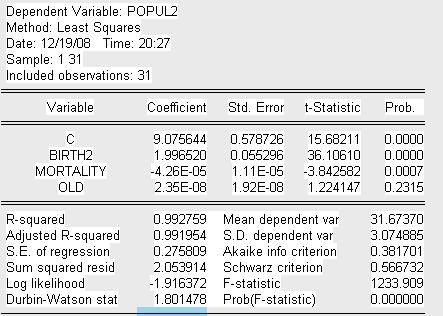
Где:

POPUL2=ln (population^2)

BIRTH2=ln(birth).

Оценим значимость коэффициентов уравнения регрессии. Для этого оценим t-статистику:

Найдем критическое значение t-статистики на уровне значимости

()

После проведенного теста можно сделать вывод о наличии гетероскедастичности по переменной Birth в следствие того, что коэффициент  при данной переменной является значимым.

Представим вспомогательную модель 2 теста Парка:

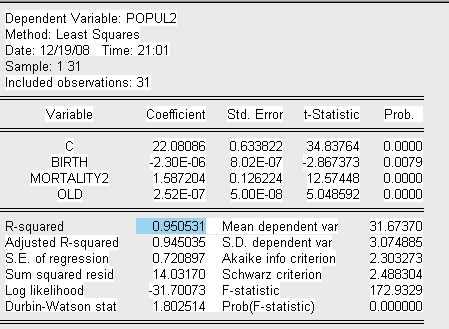
Где:

POPUL2=ln (population^2)

MORTALITY2=ln(mortality).

Запишем уравнение вспомогательной модели 2:

Оценим значимость коэффициентов уравнения регрессии. Для этого оценим t-статистику. Найдем критическое значение t-статистики на уровне значимости ()

После проведенного теста можно сделать вывод о наличии гетероскедастичности по переменной Mortality в следствие того, что коэффициент  при данной переменной является значимым.

Представим вспомогательную модель 3 теста Парка:

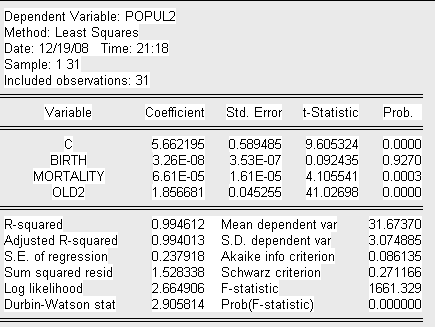
Где:

POPUL2=ln (population^2)

OLD2=ln(old).

Запишем уравнение вспомогательной модели 2:

Оценим значимость коэффициентов уравнения регрессии. Для этого оценим t-статистику. Найдем критическое значение t-статистики на уровне значимости ()

После проведенного теста можно сделать вывод о наличии гетероскедастичности по переменной Old в следствие того, что коэффициент  при данной переменной является значимым.

Оценив каждую переменную по тесту парка в отдельности подтверждаем выводы сделанные ранее по тесту Вайта о гетероскедастичности исходной модели.

Теперь используем тест Бреуша-Пагана для окончательного подтвержения гетероскедастичности. Для начала строим временной ряд квадратов остатков, деленных на величину

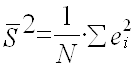
а затем строим для него саму регрессионную модель.

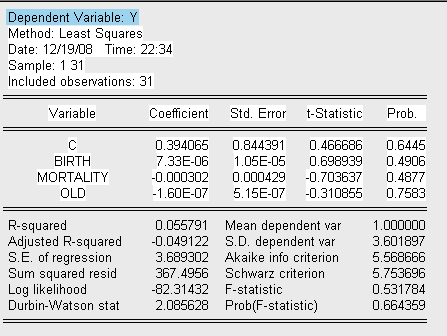
Находим необходимые для анализа параметры вспомогательной регрессии:

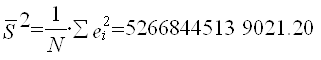
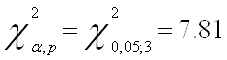
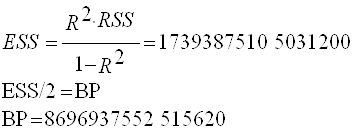
Делаем вывод об очевидном присутствии в модели гетероскедастичности, так как

>>

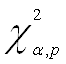
Устранение гетероскедастичности в модели

После проведения тестов Вайта, Бреуша-Пагана-Годфри и Парка было выявлено очевидное наличие проблемы гетероскедастичности остатков в базовой модели регрессии. Приступим к ее устранению при помощи веса, выбранного соответственно тесту Бреуша-Пагана. Предпологаем форму выявленной гетероскедастичности:

Вес:

Оцененная с помощью метода взвешанных наименьших квадратов базовая регрессия выглядит следующим образом:

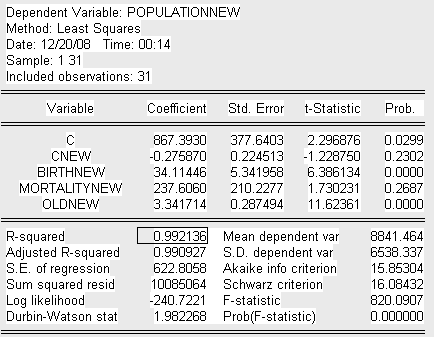
Получим следующее уравнение построенной модели-NEW:

Где переменные, скорректированные на вес:

PopulationNEW – общая численность населения на начало 2008г. (чел.),

cNEW – константа базовой модели, деленная на вес,

BirthNEW – численность рожденных детей за 2007г. (чел.),

MortalityNEW – численность умерших за 2007г. (чел),

OldNEW – численность населения в возрасте от 65 лет и старше (чел.).

Проверим на значимость коэффициенты уравнения регрессии. Для этого оценим t-статистику. Используем в данном случае уровень значимости . Тогда критическое значение t-статистики соответственно:

Если значения t-статистик рассматриваемых переменных больше критического значения (критерий Стьюдента), следовательно делаем вывод о их значимости. Лишь одна переменная, являющаяся в прошлой базовой модели константой в данном случае незначима, что логично, ведь она не имеет реального смысла, т.е. не описывает реальным образом объясняемую переменную. По анализу исследованных t-статистик и коэффициента детерминации R-квадрат делаем предварительный вывод об адекватности построенной модели.

Продолжая оценивать общее качество модели, используем критерий Фишера:

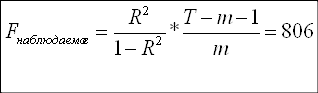
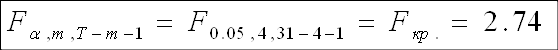
Н0: R-квадрат=0

Н1: R-квадрат>0

Так как F-наблюдаемое больше F-критического, принимаем гипотезу Н1, согласно которой модель адекватна.

Проверим модель на присутствие автокорреляции. Для этого будем использовать тесты Бреуша-Годфри и Дарбина-Уотсона.

1) Первоначально воспользуемся тестом Бреуша-Годфри и оценим модель на присутствие автокорреляции по трем лагам:

Запишем значение  распределения для последующего сравнения с Obs* R-squared:

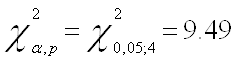
Приведем результаты теста с lag = 1:

с lag = 2:

с lag = 3:

Сделаем выводы об отсутствии серийной корреляции, так как во всех трех случаях Obs* R-squared меньше

а P-вероятность статистики Бреуша-Годфри больше уровня значимости

()

2) Воспользуемся также тестом Дарбина-Уотсона:

Приведем значение статистики:

Значения критических точек

при уровне значимости :

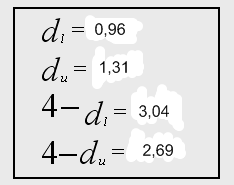
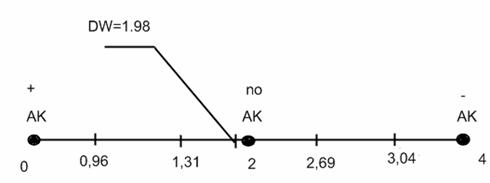
Делаем вывод об отсутствии автокорреляции, т.к. значение статистики D-W в данном случае близко к 2.

Проверим скорректированную модель на наличие гетероскедастичности с помощью теста Вайта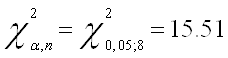

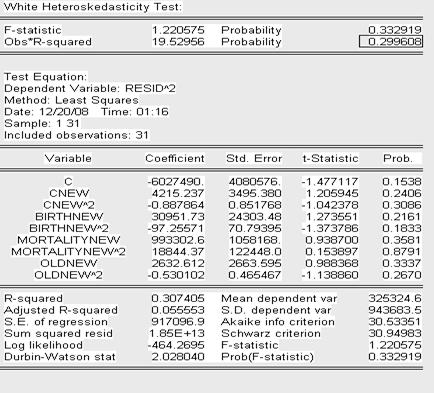
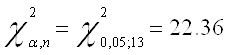
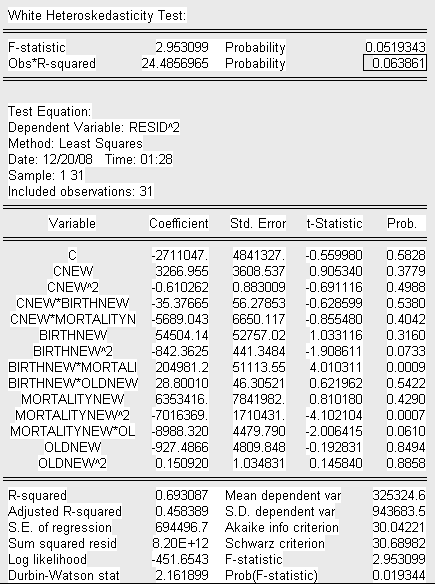
Т.к. значение P- вероятности в обоих случаях теста Уайта (no cross terms/ cross terms) больше уровня значимости

()

и Obs* R-squared превышает

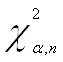
то принимаем гипотезу об отсутствии гетероскедастичности в модели (гомоскедастичность).

Заключение

В моей курсовой работе я построила регрессионную модель по реальным данным. Я разбиралась с моделью зависимости общей численности населения от показателей рождаемости, смертности и численности пожилого населения, их влиянием друг на друга и на объясняемую переменную. Так как целью моей работы являлось проверить, как работают на практике тесты Уайта и Бреуша-Пагана-Годфри и Парка, то я использовала пространственные данные, которые позволяют наиболее наглядно проиллюстрировать проблему гетероскедастичности и способы ее устранения.

В работе достаточно наглядно продемонстрирована работа тестов для выявления гетероскедастичности, также удалось решить задачу с выбором веса для ВНК.

В ходе курсовой работы мне удалось скорректировать модель с помощью метода взвешенных наименьших квадратов, правильно подобрав вес при помощи теста Бреуша-Пагана, поскольку тест Вайта, к примеру, не дает нам точного ответа на вопрос о весе для ВНК. Построенная в конце моего исследования модель-NEW значима и является качественной, остатки ее в свою очередь гомоскедастичны.

Список использованных источников:

1.  Бородич С.А. Вводный курс эконометрики: Учеб. пособие. – Мн.; БГУ, 2000. – 209, 227, 245 с.

2.  Бородич С.А. Эконометрика: Учеб. пособие. – Мн.; Новое знание, 2006. – 237, 238 с.

3.  Доугерти К. Введение в эконометрику: Пер. с англ. – М.; ИНФРА-М, 1997.

4.  Данные Eurostat http://epp.eurostat.ec.europa.eu/potal.