Сущность и классификация экономико-математических моделей
Методики моделирования программы развития сельскохозяйственного предприятия в работах ученых экономистов
<=X1<= X
Порядок пополнения запасов (или срок выполнения заказа). Речь идет об интервале времени между моментом размещения заказа и его поставкой
Постановка экономико-математической задачи
Обоснование исходной информации задачи
Планируемое поголовье лошадей соответствует фактическому;
Навигация
Методики моделирования программы развития сельскохозяйственного предприятия в работах ученых экономистов
Методика математического моделирования программы развития сельскохозяйственного предприятия
67449
знаков
19
таблиц
0
изображений
1.3 Методики моделирования программы развития сельскохозяйственного предприятия в работах ученых экономистов
В экономических исследованиях издавна применялись простейшие математические методы. В хозяйственной жизни широко используются геометрические формулы. Так, площадь участка поля определяется путем перемножения длины на ширину или объем силосной траншеи - перемножением длины на среднюю ширину и глубину. Существует целый ряд формул и таблиц, облегчающих хозяйственным работникам определение тех или иных величин.[Кравченко 6].
В 60-е годы нашего столетия развернулась дискуссия о математических методах в экономике. Например, академик Немчинов выделял пять базовых методов исследования при планировании:
1) балансовый метод;
2) метод математического моделирования;
3) векторно-матричный метод;
4) метод экономико-математических множителей (оптимальных общественных оценок);
5) метод последовательного приближения.[немчинов].
В то же время академик Канторович выделял математические методы в четыре группы:
- макроэкономические модели, куда относил балансовый метод и модели спроса;
- модели взаимодействия экономических подразделений (на основе теории игр);
- линейное моделирование, включая ряд задач, немного отличающихся от классического линейного программирования;
- модели оптимизации, выходящие за пределы линейного моделирования (динамическое, нелинейное, целочисленное, и стохастическое программирование). [Контрович].
По широте применения различных методов в реальных процессах планирования несомненным лидером является метод линейной оптимизации, который был разработан академиком Канторовичем в 30-е годы ХХ-го века. Чаще всего задача линейного программирования применяется при моделировании организации производства. Вот как по Канторовичу выглядит математическая модель организации производства:
В производстве участвуют M различных производственных факторов (ингредиентов) - рабочая сила, сырье, материалы, оборудование, конечные и промежуточные продукты и др. Производство использует S технологических способов производства, причем для каждого из них заданы объемы производимых ингредиентов, рассчитанные на реализацию этого способа с единичной эффективностью, т.е. задан вектор ak = (a1k, a2k,..., amk ), k = 1,2...,S, в котором каждая из компонент aik указывает объем производства соответствующего ( i-го ) ингредиента, если она положительна; и объем его расходования, если она отрицательна ( в способе k ).
Выбор плана означает указание интенсивностей использования различных технологических способов, т.е. план определяется вектором x = (x1, x2,..., xS ) c неотрицательными компонентами [Контрович].
Обычно на количества выпускаемых и затрачиваемых ингредиентов накладываются ограничения: произвести нужно не менее, чем требуется, а затрачивать не больше, чем имеется. Такие ограничения записываются в виде
s
S a ikxk > bi ; i=1,2,...,m.
k=1
Если i > 0, то неравенство означает, что имеется потребность в ингредиенте в размере i, если i < 0,то неравенство означает, что имеется ресурс данного ингредиентов размере - i =¦ i¦. Далее предполагается, что использование каждого способа, связанного с расходом одного из перечисленных ингредиентов или особо выделенного ингредиента в количестве Ck при единичной интенсивности способа k. В качестве целевой функции принимается суммарный расход этого ингредиента в плане.
s
f(x) = S ckxk.
k=1
Теперь общая задача линейного программирования может быть представлена в математической форме. Для заданных чисел aik, ck, и bi найти
s
min S ckxk
k=1
при условиях
k > 0, k = 1,2,...,s [1]
s
S aikxk > bi, i = 1,2,...,m [2]
k=1
План, удовлетворяющий условиям [1] и [2], является допустимым, а если в нем, кроме того, достигается минимум целевой функции, то этот план оптимальный.
Задача линейного программирования двойственна, то есть, если прямая задача имеет решение, (вектор x =( x1, x2,..., xk)), то существует и имеет решение обратная задача основанная на транспонировании матрицы прямой задачи. Решением обратной задачи является вектор y = ( y1, y2... ,ym) компоненты которого можно рассматривать как объективно обусловленные оценки ресурсов, т.е. оценки, показывающие ценность ресурса и насколько полно он используется. [Контрович]
На основе объективно обусловленных оценок американским математиком Дж. Данцигом - был разработан симплекс-метод решения задач оптимального программирования. Этот метод весьма широко применяется. Алгоритм его весьма детально проработан, и даже составлены прикладные пакеты программ, которые применяются во многих отраслях планирования.
Его идея состоит в следующем: вначале достигается опорное решение поставленной задачи, т.е. допустимый вариант, удовлетворяющий всем ограничениям. Затем, проделывая ряд последовательных шагов, сводящихся к выполнению элементарных алгебраических преобразований, получают новое решение. Оно лучше или, по крайней мере, не хуже предшествующего. После конечного числа шагов (итераций) либо устанавливают неразрешимость задачи, либо опорный план является оптимальным.
Необходимо отметить, что симплекс метод работает только для системы линейных уравнений в каноническом виде, в которой должна быть предварительно записана исходная задача.
Решение задачи включает поиск опорного и нахождение оптимального решения. Признаки опорного решения – это наличие положительных свободных членов. В случае его отсутствия поступаем следующим образом:
1 – выбираем любой отрицательный свободный член;
2 – находим любой отрицательный коэффициент в строке отрицательного свободного члена;
3 – проводя деление коэффициентов столбца свободных членов на соответствующие коэффициенты столбца с выбранным отрицательным элементом, находим наименьшее положительное значение, которое укажет на разрешающий коэффициент.
После выбора разрешающего элемента симплексное преобразование выполняется по следующим правилам:
1. Новый коэффициент вместо разрешающегося равен 1, деленной на разрешающийся коэффициент. При этом новыми будут называться коэффициенты следующей симплексной таблицы по отношению к предыдущей;
2. Новые коэффициенты строки разрешающегося элемента равны предыдущим, деленным на разрешающий;
3. Новые коэффициенты столбца разрешающегося элемента равны предыдущим, деленным на разрешающий элемент, взятый с противоположным знаком;
4. Новые коэффициенты, не стоящие в строке или столбце разрешающегося элемента, равны частному от деления разности произведения коэффициентов главной и побочной диагоналей на разрешающий элемент.
Все результаты расчетов элементов заносятся в симплекс-таблицу. [Колеснев]
Несмотря на широту применения метода линейного программирования, он учитывает лишь три особенности экономических задач - большое количество переменных, ограниченность ресурсов и необходимость целевой функции. Конечно, многие задачи с другими особенностями можно свести к линейной оптимизации, но это не дает нам права упустить из виду другой хорошо разработанный метод математического моделирования - динамическое программирование. По сути, задача динамического программирования является описанием многошаговых процессов принятие решений. Задача динамического программирования можно сформулировать следующим образом :
имеется некоторое количество ресурса х, которое можно использовать N различными способами. Если обозначить через хi количество ресурса, используемое i-m способом, то каждому способу сопоставляется функция полезности (хi), выражающая доход от этого способа. Предполагается, что все доходы измеряются в одинаковых единицах и общий доход равен сумме доходов, полученных от использования каждого способа.
Теперь можно поставить задачу в математической форме. Найти
max y1(x1)+ y2(x2)+ ... + yn(xn)
(общий доход от использования ресурсов всеми способами) при условиях:
- выделяемые количества ресурсов неотрицательны;
[1] x1 > 0,..., xN > 0
- общее количество ресурсов равно x .
[2] x1 + x2 + ... + xN = x
Для этого общей задачи могут быть построены рекуррентные соотношения
¦1(x) = max {j1(x1)},
Похожие работы
... углекислотные огнетушители ОУ-ОУ-5, пенные, ОП-5. 4.2 Мероприятия по улучшению условий и безопасности труда В результате анализа состояния охраны труда в ОАО «Смолевичский райагросервис» предлагаем провести следующие мероприятия: · согласно положения «О планировании разработке мероприятий по охране труда», утвержденного постановлением Министерства труда Республики Беларусь от 23.10.2000 ...
... эффективности использования ресурсов предприятия 2.1 Постановка экономико-математической задачи Сельскохозяйственное предприятие представляет собой социально-экономическую систему с определенными соотношениями и пропорциями ее подразделений и взаимосвязями с другими предприятиями АПК. Рассматриваемая модель специализации и сочетания отраслей - комплексная. Она учитывает все составляющие ...
... использовать наличные и дополнительно вовлекаемые производственные ресурсы и получить наивысший экономический эффект [2]. В результате решения экономико-математической задачи оптимизации производственной структуры сельскохозяйственного предприятия определяют: состав и размеры основных и дополнительных отраслей хозяйства; посевные площади различных культур и поголовье скота; объемы производства ...
... к нормальной категории. Результаты решения параметрической задачи, полученные для четырех рассмотренных вариантов, представлены в таблице 11. Таблица 11 – Результаты моделирования устойчиво земледелия сельскохозяйственного предприятия южной лесостепи Параметры модели Варианты модели Общие показатели Среднегодовая прибыль, тыс.руб. 222927 23841 21286 17346 Площадь, га: пара 2466 2378 ...
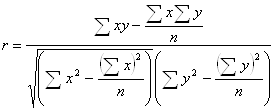
0 комментариев