Навигация
Теорема Гаусса і її використання
3. Теорема Гаусса і її використання
У випадках розрахунків напруженості електричного поля не- точкових зарядів, виникають певні труднощі. В таких випадках напруженість електричного поля розраховують за допомогою методу суперпозиції. Для цього, просторово розміщені заряди ділять на точкові й методом інтегрування (принцип суперпозиції), знаходять відповідну напруженість. Покажемо це на прикладах:
Приклад 1. Визначити напруженість електричного поля біля безмежної, рівномірно зарядженої площини з поверхневою густиною зарядів (рис. 6.7).
Скористаємось формулою напруженості точкового заряду (6.2.6)
dE = 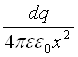 , (6.3.1)
, (6.3.1)
де dq – це заряд заштрихованої безмежно малої ділянки поверхні; x – відстань від цієї ділянки до точки А, в якій розраховується напруженість електричного поля Е.
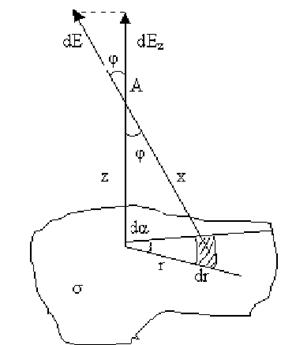
З рисунка видно, що x2 = z2 + r2, а dq = rd dr, й dEz = dEcos.
З урахуванням цих позначень одержуємо:
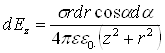 . (6.3.2)
. (6.3.2)
Але оскільки соs = ![]() , тому
, тому
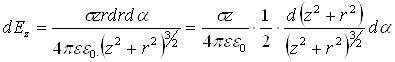 .
.
Інтегруємо цей вираз у межах: для r від 0 до ![]() ; для від 0 до 2, одержимо:
; для від 0 до 2, одержимо:
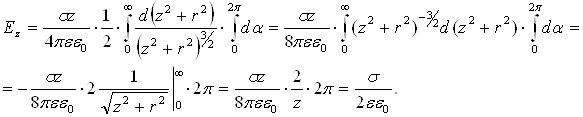
З розрахунків видно, що напруженість електричного поля біля безмежної, рівномірно зарядженої площини з поверхневою густиною зарядів , визначається досить простою формулою і не залежить від відстані до самої площини
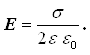 (6.3.3)
(6.3.3)
Приклад 2. Визначити напруженість електричного поля на відстані а від тонкої, досить довгої, рівномірно зарядженої, із лінійною густиною зарядів нитки або циліндра (рис 6.8).
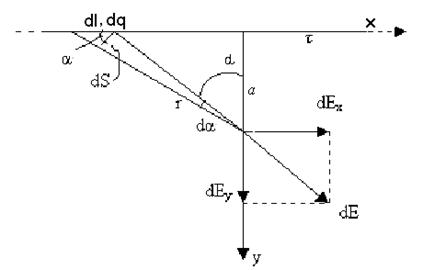
Рис. 6.8
Скористаємось формулою (6.2.6)
dE = ![]()
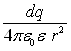 .
.
З рисунка видно, що: dq = dl і dS = rd, а також dS = dl·cos.
З урахуванням цих залежностей одержуємо величину точкового заряду:
dq = ![]() . (6.3.4)
. (6.3.4)
Тоді напруженість електричного поля у напрямі осі у Ey – буде дорівнювати
dEy= dEcos = 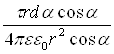 =
= 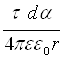 .
.
Величину радіуса-вектора r виразимо через відстань а і кут :
r = 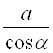 .
.
З урахуванням останнього одержимо:
dEy = 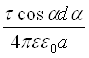 . (6.3.5)
. (6.3.5)
Інтегруємо останній вираз у межах зміни від 0 до ![]() , помноживши весь вираз на 2 (враховується друга, симетрична частина нитки).
, помноживши весь вираз на 2 (враховується друга, симетрична частина нитки).
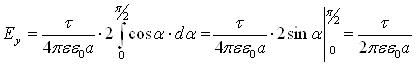 .
.
Таким чином одержано досить просту залежність напруженості електричного поля біля довгої, рівномірно зарядженої нитки або циліндра:
Е = 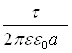 . (6.3.6)
. (6.3.6)
Паралельна складова напруженості Еx,завдяки симетричності нитки, буде дорівнювати нулю.
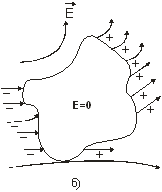
Знайдемо потік вектора ![]() напруженості електричного поля крізь замкнену поверхню ( рис. 6.9)
напруженості електричного поля крізь замкнену поверхню ( рис. 6.9)
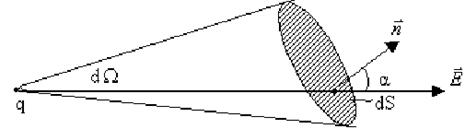
Рис. 6.9
![]() , (6.3.7)
, (6.3.7)
де ![]() - величина площі заштрихованої поверхні,
- величина площі заштрихованої поверхні, ![]() - нормаль до поверхні (одиничний вектор).
- нормаль до поверхні (одиничний вектор).
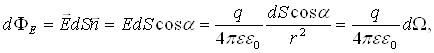
де ![]() - тілесний кут.
- тілесний кут.
Площа поверхні кулі ![]() (тут
(тут ![]() є тілесним кутом).
є тілесним кутом).
Таким чином одержуємо:
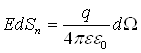 . (6.3.8)
. (6.3.8)
Інтегруємо цей вираз у межах замкнутої поверхні і повного тілесного кута для цієї поверхні, тобто
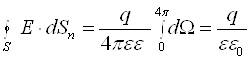 .
.
Одержаний вираз носить назву теореми Гаусса
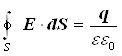 . (6.3.9)
. (6.3.9)
Якщо замкнута поверхня охоплює систему зарядів, теорема Гаусса набуде вигляду
![]() . (6.3.10)
. (6.3.10)
Потік вектора напруженості електричного поля крізь довільну замкнуту поверхню дорівнює алгебраїчній сумі всіх зарядів у середині цієї поверхні, поділених на 0.
Покажемо на прикладах, як використовується теорема Гаусса у найпростіших випадках.
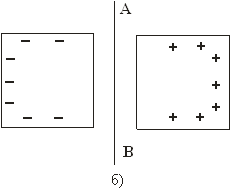
Приклад 1. Електричне поле біля безмежної, рівномірно зарядженої, із поверхневою густиною зарядів σ, площини ( рис. 6.10).
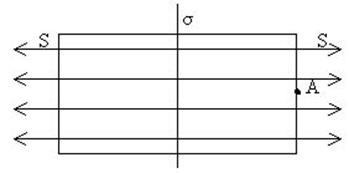
Рис. 6.10
На рисунку заряджена площина спроектована перпендикулярно до площини листка. Замкнена поверхня є циліндром із площею торців S. Потік вектора напруженості в даному випадку слід розрахувати лише крізь торці. Лінії напруженості електричного поля паралельні до бокової поверхні, а тому потоку не створюють, тобто
![]() . (6.3.11)
. (6.3.11)
За теоремою Гаусса
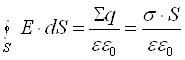 . (6.3.12)
. (6.3.12)
Прирівнявши праві сторони (6.3.11) і (6.3.12) одержимо:
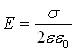 .
.
Цей висновок збігається з формулою (6.3.3).
Приклад 2. Електричне поле на відстані a від довгої, рівномірно зарядженої з лінійною густиною зарядів τ, нитки (рис. 6.11).
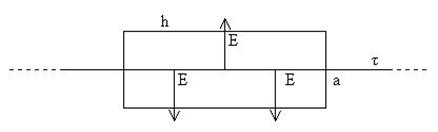
Рис. 6.11
На рисунку замкнуту поверхню вибрано у вигляді циліндра радіусом а і довжиною h. Потік силових ліній слід розглядати лише крізь бокову поверхню, так як торці перпендикулярні до нитки й паралельні до напрямку силових ліній електричного поля. (Потік крізь торці в цьому випадку дорівнює нулю).
![]() . (6.3.13)
. (6.3.13)
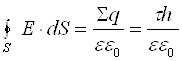 . (6.3.14)
. (6.3.14)
Прирівнюємо праві частини (6.3.13) і (6.3.14), одержимо
![]() =
=![]() .
.
Звідки
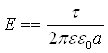 , (6.3.15)
, (6.3.15)
що збігається з формулою (6.3.6)
Висновок. Теорема Гаусса значно спрощує розрахунки, але має дуже вузькі рамки використання. Більш загальним, універсальним методом розрахунків напруженості електричного поля є метод суперпозиції, який у кінцевому випадку зводиться до інтегрування.
Похожие работы
... cell – електролітична комірка. 13. Electromagnetic induction – електромагнітна індукція. 14. Electron – електрон. 15. Electroscope – електроскоп. 16. Electrostatic – електростатика. 17. Emanation – ви промінювання. 18. Energy density – густина енергії. 19. Energy – енергія. 20. Equipotential surface – еквіпотенціальна поверхня. ...
... ? 2.27 У якому напрямку при теплообміні двох тіл передається теплова енергія? Чи можна створити вічний двигун? 2.28 Чи залежить внутрішня енергія тіла від температури? 2.29 1, 2 та 3 закони термодинаміки. 2.30 Як зміниться температура газу у циліндрі при його різкому стисканні поршнем? Чому? 2.31 Запишіть формулу визначення роботи газу при його розширенні. Чи може газ виконувати механічну ...
... 2. Савельев И.В. Курс физики, т.1, Курс общей физики.-М.: 1989. § 9-12 3. Трофимова Т.И. Курс физики,-М.: Высшая школа, 1985, 432 с. § 83, 86 План лекції з навчальної дисципліни ФІЗИКА Тема ЗАКОНИ ПОСТІЙНОГО СТРУМУ ОРГАНІЗАЦІЙНО-МЕТОДИЧНІ ВКАЗІВКИ ДО ПРОВЕДЕННЯ ЛЕКЦІЇ При вивченні постійного електричного струму, необхідно враховувати, що основні поняття постійного струму курсантам ві ...
... ж) жінки, які працюють у сільськогосподарському виробництві та виховали п'ятеро і більше дітей, - незалежно від віку і трудового стажу, в порядку, що визначається Кабінетом Міністрів України; · з) водії міського пасажирського транспорту (автобусів, тролейбусів, трамваїв) і великовагових автомобілів, зайнятих у технологічному процесі важких і шкідливих виробництв: · чоловіки - після ...
0 комментариев