Навигация
Для трьох будь-яких елементів групи вірним є сполучний закон, або закон асоціативності: (А ´ В) ´ С = А (В ´ С)
16287
знаков
6
таблиц
2
изображения
2. Для трьох будь-яких елементів групи вірним є сполучний закон, або закон асоціативності: (А ´ В) ´ С = А (В ´ С).
3. Для кожного елементу множини існує обернений елемент, який належить тій чи іншій множині: А · А–1 = Е.
4. В кожній групі є операція ідентичності Е, яка відповідає повороту на 360°. В цьому випадку для будь-якої операції виконується співвідношення: А ´ Е = Е ´ А = А.
Ці чотири правила називаються груповими аксіомами.
З метою визначення усіх симетричних перетворень об’єкту відповідної точкової групи симетрії користуються так званим квадратом Кейлі, що являє собою таблицю взаємного множення всіх пар симетричних перетворень. Операції симетрії записуються у верхньому рядку квадрата і в лівому його стовбчику. Добутки операцій записують у клітинках перетину рядів і стовбчиків таблиці. Для прикладу наведемо квадрат Кейлі для точкової групи С2v(mm2), (L22P)
Визначимо набір операцій симетрії – (4) – 1 (Е), 2z, mx, my.
| 1 | 2z | mx | my | |
| 1z | 1 | 2z | mx | my |
| 2z | 2z | 1 | my | mx |
| mx | mx | my | 1 | 2z |
| my | my | mx | 2z | 1 |
Добуток будь-яких двох операцій симетрії дорівнює третій операції симетрії, що належить цій же групі.
Квадрат Кейлі для точкової 32 (L33L2) – 6 операцій симетрії.
| E | 31 | 32 | 2x | 2y | 2u | |
| Е | E | 31 | 32 | 2x | 2y | 2u |
| 31 | 31 | 32 | E | 2y | 2u | 2x |
| 32 | 32 | E | 31 | 2u | 2x | 2y |
| 2х | 2x | 2u | 2y | E | 32 | 31 |
| 2у | 2y | 2x | 2u | 31 | E | 32 |
| 2u | 2u | 2y | 2x | 32 | 31 | E |
Якщо міє елементами двох груп є взаємно-однозначна відповідність (добуток двох будь-яких елементів одної групи відповідає добутку двох елементів іншої групи, вони називаються ізоморфними.
Всі симетричні операції групи симетрії складають її симетричне зображення. Наприклад, в групу симетрії mmmbL23PC входять 8 операцій симетрії: Е, 2х, 2у, 2z, C(
), mx, my, mz. Порядок групи 8. Вони складають симетричне зображення групи.
У загальному вигляді зображення Г групи G подається у вигляді сукупності матриць, що відповідають всім операціям симетрії цієї групи.
Розглянемо зображення операцій симетрії точкової групи С2v на одиничний вектор 
, направлений вздовж осі х. Точкова група С2v має чотири операції симетрії: Е, С2, mx, my.
Результати перетворення координат вектора прийнято представляти за допомогою таблиць характерів. Якщо напрямок вектора при проведенні операцій симетрії не змінюється, то характер позначається +1, якщо змінюється, то –1.
1) Операція Е не змінить напрям вектора, тому характер цієї операції симетрії позначився +1.
2) 2z – поворот вектора на 180° вздовж осі z змінить координату вектора на протилежну. Характер цієї операції позначається –1.
3) Операція my (площина перпендикулярна до осі у); відбиття у цій площині не змінив напрямок вектора ; характер операції +1.
4) Операція mx (площина симетрії перпендикулярна осі х); відбиття у цій площині змінить напрямок вектора на протилежний. Характер операції симетрії –1.
Результати перетворення координат вектора прийнято представляти за допомогою таблиці характерів.
Розглянемо характери операцій симетрії вектора хуz в точковій групі С2v.
1) Е не змінить напрямок вектора хуz. Характер операції симетрії в цьому випадку представляється як сума коефіцієнтів хуz = 1 + 1 + 1 = 3.
2) 2z координату х і у змінить на протилежні, а z залишиться без зміни: –1–1+1 = –1.
3) Операції mx: х = х, у = – у, z = z; +1–1+1 = +1.
4) Операція mу: х = – у, у = у, z = z; –1+1+1 = +1.
| Е | 2z | mx | my |
| 1 | –1 | 1 | –1 |
| 1 | –1 | 1 | +1 |
| 1 | +1 | +1 | +1 |
| 3 | –1 | +1 | +1 |
Повне або приведене представлення цих операцій теж можемо представити у таблиці:
Е 2z mx my
3 –1 +1 +1.
Приведене представлення можна розкласти на суму неприведених представлень.
Симетрія молекул і нормальні коливання. Будь-яка молекула відноситься до певної точкової групи, тобто володіє певним набором елементів симетрії. Повна сукупність операціїй симетрії приводиться в таблицях типів симетрії і характерів представлень.
При коливаннях молекул можливі тільки певні комбінації властивостей симетрії зміщеної від рівноважної конфігурації.
Нормальні коливання називаються симетичними (s) по відношенню до даної операції симетрії, якщо при її виконанні вектори зміщень атомів не змінюють знак і абсолютне значення (домножуються на +1).
Антисиметричне коливання (аs) відносно операції симетрії є таким, коли при її виконанні знак зміщень змінюється на протилежний (домножується на –1).
Нормальне коливання, яке є симетричним відносно всіх операцій симетрії даної точкової групи називається повносиметричним.
Всі інші типи нормальних коливань неповносиметричні: два (Е) або три (F) вироджені.
При невироджених коливаннях операції симетрії переводять одну форму коливань в іншу, тобто вектори зміщень домножуються на числа не всі рівні 1 або всі нерівні 1.
Повна характеристика типу симетрії нормального коливання описується його відношенням до всіх операцій симетрії даної точкової групи.
Невироджені типи симетрії позначаються символами А і В. При цьому буквою А позначають коливання симетрії відносно виділеної головної осі, орієнтованої вершиною В-коливання антисиметричні відносно такої осі.
Підстрочні індекси g і u при А і В позначають симетричні і антисиметричні коливання по відношенню до операції інверсії в центрі (с). Підстрочні цифрові індекси 1 і 2 симетричний і антисиметричний тип коливань по відношенню до операції відбиття у вертикальній площині σv.
Надстрочні індекси – один штрих (¢) або два штриха (²) при буквах – позначають симетричний і антисиметричний типи коливань відносно відбиття в горизонтальній площині σh перпендикулярної головної осі симетрії.
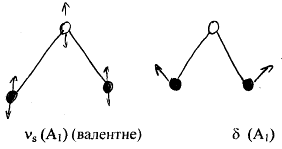
3N-6 = 3 · 3 – 6 = коливання.
(С2 σ1 σ2; Е) – С2v.
ns – симетричне валентне;
d – деформаційне.
Таблиця типів симетрії і характерів незвідних представлень групи С2v
| С2v | Е | С2(z) | σv(xz) | σv(yz) |
| A1 | 1 | 1 | 1 | 1 |
| A2 | 1 | 1 | –1 | –1 |
| B1 | 1 | –1 | 1 | –1 |
| B2 | 1 | –1 | –1 | 1 |
Коливання атомів у молекулі, що супроводжується зміною довжини зв’язків, називають валентними, а коливання, що супроводжуються зміною валентних кутів – деформаційними. Якщо при коливаннях центр між молекулами не зміщується, то такі коливання називають нормальними.
Похожие работы
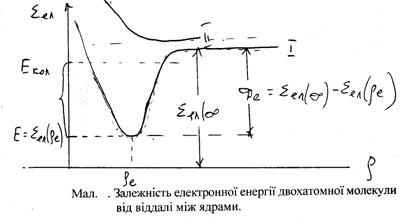
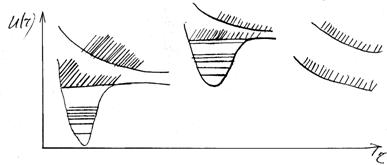
... в основному легкий. Наприклад, у зв’язку С–Н маса атома С у 12 раз більше маси атома Н, тому атом С залишається практично у спокої, а коливається Н. Електронні спектри молекул До основних характеристик кожного електронного стану молекули відносяться енергія, хвильова функція, степінь виродження, мультиплетність і час життя. Енергія молекули в заданому стані є функцією ядерної конфігурації, ...
... · NA, де r – питома вага речовини; М – молярна маса речовини = . Якщо врахувати орієнтаційний дипольний момент молекул у зовнішньому електричному полі, то рівняння Клаузиуса-Масотті набуває вигляду = . Це рівняння називають рівнянням Дебая. Поведінка речовин у змінному електричному полі. Рефракція. При дії на молекули діелектрика змінного поля поляризація залежить від зміни поля. ...
... з атомів одного елемента. Хімічною сполукою (складною речовиною) називають індивідуальну речовину, молекули якої складаються з двох або більше елементів. Таким чином, елементарною часткою в класичній теорії будови речовини є атом. А атоми в свою чергу формують хімічні частки – молекули. Тому важливим питанням у класичній теорії будови речовини є питання про будову молекул. На час створення ...
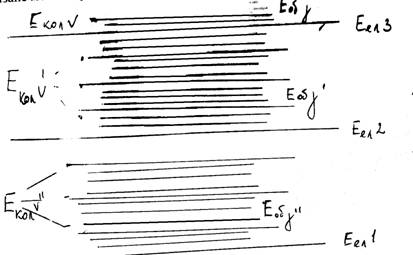
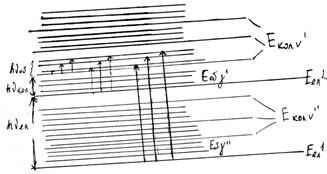
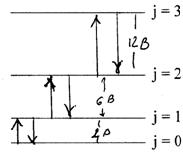
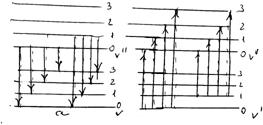
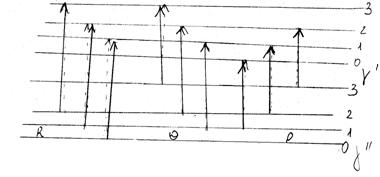
... в інший. Як уже вказувалося, при електронному збудженні молекули Еел збільшується; це приводить до збільшення моменту інерції і до зменшення обертової постійної. Тому В¢ < В². При електронних переходах в загальному випадку для обертового квантового числа у має місце звичайне правило відбору для моментів кількості руху: Dу = 0; ±1. Для зміни обертової енергії при електронно-коливних ...
0 комментариев