Финансовая математика

вариант 1

1.  В чем заключается принцип неравноценности денег?

Сумма денег независимо от их происхождения и назначения в финансовых операциях обязательно связываются с некоторыми моментами или интервалами времени. Фактор времени, особенно в долгосрочных финансовых операциях, играет не менее важную роль, чем размеры самих денежных сумм.

Необходимость учета этого фактора выражается в виде принципа неравноценности денежных сумм, относящихся к различным моментам времени, даже если эти суммы одинаковы. Неравноценность двух одинаковых денежных сумм, относящихся к разным моментам времени, определяются тем, что любую сумму денег можно инвестировать и получить доход от этих инвестиций. Полученный доход можно реинвестировать и т.д.  В наиболее общем виде принцип неравноценности денег можно сформулировать так: сегодняшние деньги ценнее будущих, а будущие поступления менее ценны, чем современные.

2.  В каких случаях используются простые проценты?

Простые проценты чаще всего используются при краткосрочных (длительностью менее года) операциях. Проценты начисляются один раз в конце срока вклада.

В банковских договорах процентная ставка указывается за год. Для других периодов (например, месяца) нужно перевести срок вклада в дни использовать для расчета простых процентов следующую формулу:

Fv = Sv * ( 1 + R * (Td / Ty) ), где

Fv — итоговая сумма;

Sv — начальная сумма;

R — годовая процентная ставка;

Td — срок вклада в днях;

Ty — количество дней в году.

3.  Опишите дисконтирование по сложным процентам. Приведите примеры.

Дисконтирование стоимости (discounting) — процесс приведения будущей стоимости денежных средств (вклада) к их настоящей стоимости путем исключения из будущей суммы соответствующей величины процента (дисконта). Посредством такой финансовой операции достигают сопоставимости текущей стоимости предстоящих денежных потоков.

Сложный процент — сумма дохода, начисляемого в каждом интервале, которую не выплачивают, а присоединяют к основной сумме капитала (вклада) в последующем платежном периоде.

Современная величина и процентная ставка, по которой проводится дисконтирование, находятся в обратной зависимости: чем выше процентная ставка, тем при прочих равных условиях меньше современная величина.

В той же обратной зависимости находятся современная величина и срок финансовой операции: чем выше срок финансовой операции, тем меньше при прочих равных условиях современная величина.

Итак, рассмотрим использование при математическом дисконтировании сложных процентных ставок:

  (1)

Если проценты будут начисляться m раз в году, то формула (1) примет вид:

  (2)

Пример 1

Банк производит начисление процентов на внесенную сумму по сложной процентной ставке, равной 20 % в год. Какую сумму следует положить на депозит при условии, что вкладчик рассчитывает получить 10 000 тыс. руб. через 10 лет? Требуется рассмотреть два варианта начисления процентов — ежегодное и ежеквартальное.

При ежегодном начислении процентов по формуле (1):

PV = 10 000 / (1 + 0,2)¹⁰ = 1615,1 тыс. руб.

При ежеквартальном начислении процентов по формуле (2):

PV = 10 000 / (1 + 0,2 / 4)⁴⁰ = 1420,5 тыс. руб.

Использование сложной учетной ставки

Для расчета операции дисконтирования по сложной учетной ставке используется формула:

PV_n = FV_n(1 – d)ⁿ.  (3)

Пример 2

Владелец векселя номинальной стоимостью 500 тыс. руб. и периодом обращения 1,5 года предложил его банку сразу для учета, то есть за 1,5 года до погашения. Банк согласился учесть вексель по сложной учетной ставке 20 % годовых. Требуется определить дисконт, полученный банком, и сумму, выданную владельцу векселя.

Используя формулу (3), находим:

PV = 500 (1 – 0,2)^1,5 = 357,77 тыс. руб.

Дисконт банка составит: 500 – 357,77 = 142,23 тыс. руб.

Для данных условий определим сумму, которую получил бы владелец векселя, если бы банк произвел учет векселя по простой учетной ставке 20 %. Для этого используем формулу (5):

PV = 500 (1 – 0,2 × 1,5) = 350 тыс. руб.

Дисконт банка составит 500 – 350 = 150 тыс. руб.

Таким образом, банку выгоднее учитывать вексель по простой учетной ставке.

Если дисконтирование по сложной учетной ставке производится m раз в году, расчетная формула будет иметь следующий вид:

  (4)

Пример 3

Сохраним условия предыдущего примера, но пусть расчет дисконтирования производится ежеквартально, то есть m = 4.

По формуле (4) получим:

PV = 500 (1 – 0,2 / 4)⁶  = 367,55 тыс. руб.

Дисконт банка составит: 500 – 367,55 = 132,45 тыс. руб.

Доход банка при ежеквартальном дисконтировании будет меньше, чем при ежегодном дисконтировании, на: 142,23 – 132,45 = 9,78 тыс. руб.

При дисконтировании с начислением процентов за периоды менее года может использоваться понятие «эффективная сложная учетная ставка». Эффективная сложная учетная ставка, эквивалентная сложной учетной ставке при заданном значении m, определяется по формуле:

d^эф = 1 – (1 – d / m)^m. (5)

Пример 4

Долговое обязательство номинальной стоимостью 500 тыс. руб. должно быть погашено через пять лет. Сложная учетная ставка равна 20 % годовых. Начисление процентов ежеквартальное. Требуется определить настоящую величину стоимости обязательства и эффективную учетную ставку.

Используя формулы (4) и (5), получим:

PV = 500 (1 – 0,2 / 4)²⁰  = 179,243 тыс. руб.

d^эф = 1 – (1 – 0,2 / 4)⁴ = 0,18549, или 18,549 %.

Подставив значение 18,549 % в формулу (24), получим:

PV = 500 (1 – 0,18549)⁵ = 179,247 тыс. руб.

Расхождение между величинами настоящей суммы, рассчитанными по этим формулам, находятся в пределах точности расчета.

4.  Как определяется наращенная сумма ренты пренумерандо?

Рента пренумерандо отличается от обычной ренты числом периодов начисления процентов. Поэтому наращенная сумма ренты пренумерандо будет больше наращенной суммы обычной ренты в (1 + i) раз.

Такая рента реализуются сразу же после заключения контракта, т.е. первый платеж производится немедленно, а последующие платежи производятся через равные интервалы. Такие ренты (пренумерандо) также называются авансовыми, или причитающимися аннуитетами. Сумма членов такой ренты определяется по формуле:

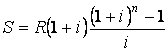  (1)

То есть сумма членов ренты пренумерандо больше наращенной суммы ренты постнумерандо в  раз, поэтому наращенная сумма ренты пренумерандо равна:

  (2)

где S - наращенная сумма постнумерандо.

5.  Как определить номинальную процентную ставку, обеспечивающую наращение реальной ценности денежных средств?

Реальная сумма (ценность) денежных средств — это оценка этой суммы с учетом изменения покупательной способности денег в связи с процессом инфляции.

Корректировка наращенной стоимости с учетом инфляции производится по формуле:

(1)

где — реальная будущая стоимость денег,

F_n — номинальная будущая стоимость денег с учетом инфляции.

Здесь предполагается, что темп инфляции сохраняется по годам.

Если r — номинальная ставка процента, которая учитывает инфляцию, то расчет реальной суммы денег производится по формуле:

, (2)

то есть номинальная сумма денежных средств снижается в (1+Т)ⁿ раза в соответствии со снижением покупательной способности денег.

В общем случае при анализе соотношения номинальной ставки процента с темпом инфляции возможны три случая:

1.  r = T: наращение реальной стоимости денежных средств не происходит, так как прирост их будущей стоимости ПОГЛОЩАЕТСЯ инфляцией

2.  r > T: реальная будущая стоимость денежных средств возрастает несмотря на инфляцию

3.  r < T: реальная будущая стоимость денежных средств снижается, то есть процесс инвестирования становится УБЫТОЧНЫМ.

Практические задания:

 

1.  Клиент поместил в банк 1000$ по ставке простого процента 12,5% на 9 лет и 5 месяцев. Вычислите общую сумму процентного дохода.

Дано:

PV=1000$

r=12,5%=0,125

n=9,5

I=?

Решение:

I = FV-PV = PV × r × n

I=1000$*0,125*9,5=1187,5$

Ответ:

Общая сумма процентного дохода за 9 лет 5 месяцев составит 1187,5$.