Расчет основных деталей и узлов

2. Расчет основных деталей и узлов

Для предварительного определения массы машин служит ГОСТ 19618-74 и типаж на эти машины. Ориентировочные массы отдельных узлов экскаватора определяются по соответствующим показателям машин-аналогов с учетом правил масштабности конструкций, установленных по теории подобия.

Для определения общих размеров машины и ориентировочных размеров ее узлов служат эмпирические формулы.

Dp = 1,75 * 1.8 = 3.15

bk = 0.9 * 0.7 = 0.63

hk = 0.5 * 0.7 = 0.35

Tk = 3.14 * 3.15 / 0.35 = 28.26

lk = 0.4 * 28.26 = 11.3

3. Расчет технико-экономических показателей машины

 

Производительность:

Эксплуатационная производительность роторных траншейных экскаваторов по выносной способности, м³/ч,

Q = 3600 nmqk_нk_в/k_р,

где n - частота вращения ротора, с^-1; m - число ковшей; q - вместимость ковша, м³; k_в - коэффициент использования машины по времени (0,7...0,85); k_н - коэффициент наполнения (0,9... 1,1); k_р - коэффициент разрыхления грунта (1,1…1,4).

Мощность:

Мощность, расходуемая на копание грунта, кВт,

Р = R_К*Q/3600,

где R_к - удельное сопротивление копанию (кПа), зависящее от категории разрабатываемого грунта; для грунтов I категории R_к ~ 100 кПА, II категории R_к ~ 200 кПА, III - R_к ~ 300 кПА, IV - R_к ~ 400 кПа.

Глубина отрываемой траншеи :

 

Rp – радиус ротора до режущих кромок;

Ho.p – разница уровней платформы экскаватора и оси вращения ротора;

4. Тестовый расчет

 

Производительность:

 

Q = (3600*n*m*qz*kv*kn)/kp = (3600*0.13*14*0.16*0.7*0.9)/1.1 = 600 m3/ч

 

Мощность необходимая для рытья траншеи:

 

P = (Rk*Q)/3600 = (100*600)/3600 = 16.6 кВm

 

5. Методы, применяемые для определения оптимального режима работы

 

5.1 Нахождение max значения производительности с помощью метода Фибоначчи

 

Предположим, что нужно определить минимум как можно точнее, т. е. с наименьшим возможным интервалом неопределенности, но при этом можно выполнить только n вычислений функции. Как следует выбрать n точек, в которых вычисляется функция? С первого взгляда кажется ясным, что не следует искать решение для всех точек, получаемых в результате эксперимента. Напротив, надо попытаться сделать так, чтобы значения функции, полученные в предыдущих экспериментах, определяли положение последующих точек. Действительно, зная значения функции, мы тем самым имеем информацию о самой функции и положении ее минимума и используем эту информацию в дальнейшем поиске.

Предположим, что имеется интервал неопределенности (x₁, x₃) и известно значение функции f(х₂) внутри этого интервала (см. рис. 5.1). Если можно вычислить функцию всего один раз в точке х*, то где следует поместить точку х₄ , для того чтобы получить наименьший возможный интервал неопределенности?

Положим x₂-x₁ = L и х₃ - x₂ = R, причем L > R, и эти значения будут фиксированы, если известны x₁, x₂, x₃. Если x₄ находится в интервале (x₁; x₂) , то:

1) если f(х₄) < f(x₂), то новым интервалом неопределенности будет (x₁; x₂) длиной x₂-x₁ = L;

2) если f(х₄) > f(х₂), то новым интервалом неопределенности будет (x₄; x₃) длиной х₃ - x₄.

 

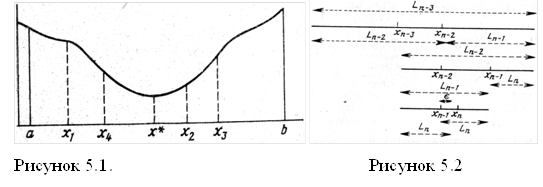
Поскольку не известно, какая из этих ситуаций будет иметь место, выберем x₄ таким образом, чтобы минимизировать наибольшую из длин х₃ - х₄ и х₂ - x₁. Достигнуть этого можно, сделав длины х₃ - x₄ и х₂ - x₁ равными, т. е. поместив х₄ внутри интервала симметрично относительно точки х₂, уже лежащей внутри интервала. Любое другое положение точки x₄ может привести к тому, что полученный интервал будет больше L. Помещая х₄ симметрично относительно х₂, мы ничем не рискуем в любом случае.

Если окажется, что можно выполнить еще одно вычисление функции, то следует применить описанную процедуру к интервалу (х_1, х₂), в котором есть значение функции, вычисленное в точке x₄, или к интервалу (x₄; x₃) , в котором уже есть значение функции, вычисленное в точке х₂. Следовательно, стратегия ясна с самого начала. Нужно поместить следующую точку внутри интервала неопределенности симметрично относительно уже находящейся там точке. Парадоксально, но, чтобы понять, как следует начинать вычисления, необходимо разобраться в том, как его следует кончать.

На n-м вычислении (рис. 5.2) n-ю точку следует поместить симметрично по отношению к (n-1)-й точке. Положение этой последней точки в принципе зависит от нас. Для того чтобы получить наибольшее уменьшение интервала на данном этапе, следует разделить пополам предыдущий интервал. Тогда точка х_n, будет совпадать с точкой х_п-1. Однако при этом мы не получаем никакой новой информации. Обычно точки х_п-1 и х_п отстоят друг от друга на достаточном расстоянии, чтобы определить, в какой половине, левой или правой, находится интервал неопределенности. Они помещаются на расстоянии є/2 по обе стороны от середины отрезка L_п-1; можно самим задать величину є или выбрать эту величину равной минимально возможному расстоянию между двумя точками. (Предположим, что в нашем примере инженер может регулировать температуру с интервалом в 1°С, поэтому є = 1.)

Интервал неопределенности будет иметь длину L_n, следовательно, L_п-1= 2 L_n – є (рис. 11, нижняя часть).

На предыдущем этапе точки х_п-1 и х_п-2 должны быть помещены симметрично внутри интервала L_п-2 на расстоянии L_п-1 от концов этого интервала. Следовательно,

 

L_п-2 = L_п-1 + L_п (рис. 5.2, средняя часть).

Из рисунка ясно, что на предпоследнем этапе х_п-2 остается в качестве внутренней точки.

Аналогично L_п-3 = L_п-2 + L_п-1 (рис. 5.2, верхняя часть)

В общем случае

 

L_j-1 = L_j+ L_j+1 при 1 < j < n.

Таким образом,

 

L_п-1 =2 L_п – ε,

L_п-2 = L_п-1+ L_п =3L_п – ε,

L_п-3 = L_п-2+ L_п-1 =5 L_п – ε_,

L_п-4 = L_п-3+ L_п-2 =8 L_п – εи т. д.

Если определить последовательность чисел Фибоначчи следующим образом:

F₀= 1, F₁ = 1 и F_k=F_k-1 + F_k-2 для k = 2,3, … , то

L_n-j=Fj₊₁^. L_n – F_j-1^. ε, j = 1,2, … , n-1

Если начальный интервал (а, b) имеет длину L₁ (= b - а), то

 

L₁=F_n^. L_n – ε ^. F_n-2,

т.е.

Следовательно, произведя n вычислений функции, мы уменьшим начальный интервал неопределенности в 1/F_n раз по сравнению с его начальной длиной (пренебрегая ε) , и это — наилучший результат.

Если поиск начат, то его несложно продолжить, используя описанное выше правило симметрии. Следовательно, необходимо найти положение первой точки, которая помещается на расстоянии L ₂ от одного из концов начального интервала, причем не важно, от какого конца, поскольку вторая точка помещается согласно правилу симметрии на расстоянии L₂ от второго конца интервала:

После того как найдено положение первой точки, числа Фибоначчи больше не нужны. Используемое значение е может определяться из практических соображений. Оно должно быть меньше L₁/F_n+1, в противном случае мы будем напрасно тратить время на вычисление функции. Таким образом, поиск методом Фибоначчи, названный так ввиду появления при поиске чисел Фибоначчи, является итерационной процедурой. В провесе поиска интервала (х₁, х₂) с точкой х₂, уже лежащей в этом интервале, следующая точка x₄ всегда выбирается такой, что х₃ - x₄ = x₂ - x₁ или х₄ - х₁ =х₃ - х₂, т. е. х₄ = x₁ - х₂ + х₃.

Если f(х₂) > f(х₄) и f(х₄) < f(х₂), то можно рассмотреть четыре случая, нахождения max функции методом Фибоначчи.

 

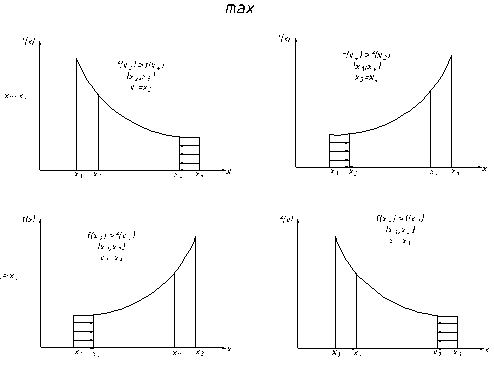
Рисунок 5.3. Четыре варианта расположения точек в интервале поиска max функции методом Фибоначчи

5.2 Определение min значения мощности методом золотого сечения

 

Не всегда можно заранее определить, сколько раз придется вычислять функцию. В методе Фибоначчи это нужно знать для определения L₂, т. е. положения начальной точки.

Метод "золотого сечения" почти столь же эффективен, как и метод Фибоначчи, однако при этом не требуется знать п — количество вычислений функции, определяемое вначале. После того как выполнено j вычислений, исходя из тех же соображений, что и ранее, записываем

 

L_j-1 = L_j+ L_j+1 .

 

Однако если п не известно, то мы не можем использовать условие L_n-1 = = 2L_n - ε. Если отношение последующих интервалов будет постоянным, т.е.

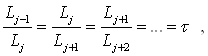
т. е. т = 1 + 1/τ.

Таким образом, τ ² - τ -1 = 0, откуда . Тогда

 и т. д.

Следовательно,

  т.е

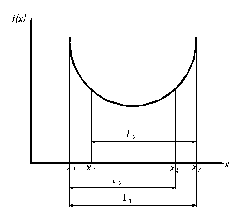
Рисунок 5.4 Поиск экстремума функции методом золотого сечения

В результате анализа двух рассмотренных значений функции будет определен тот интервал, который должен исследоваться в дальнейшем. Этот интервал будет содержать одну из предыдущих точек и следующую точку, помещаемую симметрично ей. Первая точка находится на расстоянии L₁/τ от одного конца интервала, вторая — на таком же расстоянии от другого. Поскольку , то видно, что поиск методом "золотого сечения" является предельной формой поиска методом Фибоначчи. Название "золотое сечение" произошло от названия отношения в уравнении. Видно, что L_j-1 делится на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т. е. равно так называемому "золотому отношению".

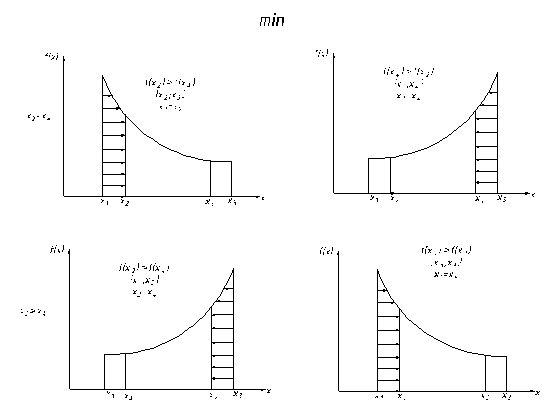
Рисунок 5.5. Четыре варианта расположения точек в интервале поиска min функции методом золотого сечения

6. Выводы и рекомендации

В процессе расчета оптимальных технико-экономических показателей работы многоковшового роторного траншейного экскаватора был проанализирован характер изменения его от частоты вращения вала n. По мнению наблюдателя определились следующие оптимальные значения технико-экономических показателей при n=0.145:

Qопт=780 м3/ч;

Pопт=21.22 кВт.

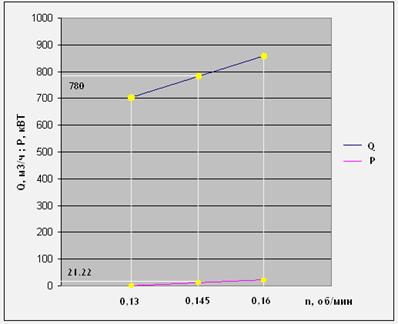
Зависимость графика Q(n) строго линейная, что позволяет увеличивать частоту вращения вплоть до значения, при котором производительность максимальна (указана в технической характеристике). Производительность может быть ограничена только потребляемой машиной мощностью изменяющейся в зависимости от частоты вращения и категории грунта.

График зависимости производительности Q и мощности Р от частоты вращения n.

7. Список литературы

 

1. конспект лекций

2. http://www.baurum.ru/_library/?cat=power_shovels&id=1209

3. Машины для земляных работ. Под общ. ред. чл.-кор. АН УССР проф. Ю. А. В е т р о в а. — 2-е изд., дораб. и доп. — Киев: Вища школа. Головное изд-во, 1981.— 384 с.

4.http://ru.wikipedia.org/wiki/Роторный_экскаватор

5.http://ru.wikipedia.org/wiki/Метод_золотого_сечения