Под случайной выборкой объема n понимают совокупность случайных величин ![]() , не зависимых между собой. Случайная выборка есть математическая модель проводимых в одинаковых условиях независимых измерений.
, не зависимых между собой. Случайная выборка есть математическая модель проводимых в одинаковых условиях независимых измерений.
Таблица 1
| 42,7; | 37,6; | 45,1; | 55,4; | 50,7; | 30,7; | 31,9; | 43,8; |
| 47,5; | 42,1; | 57,7; | 21,3; | 45,5; | 45,3; | 46,2; | 50,9; |
| 33,2; | 40,4; | 40,0; | 59,6; | 46,0; | 44,0; | 37,0; | 44,7; |
| 64,6; | 58,9; | 31,3; | 59,2; | 45,5; | 53,3; | 43,6; | 37,5; |
| 33,0; | 42,6; | 39,6; | 51,5; | 47,4; | 48,6; | 33,8; | 29,2; |
| 33,7; | 48,5; | 44,4; | 37,6; | 45,1; | 36,0; | 26,4; | 38,0; |
| 49,7; | 52,1; | 42,7; | 49,0; | 31,9; | 52,2; | 60,6; | 44,6; |
| 43,9; | 59,4; | 53,7; | 45,9. |
Упорядоченной статистической совокупностью будем называть случайную выборку величины в которой расположены в порядке возрастания ![]()
Таблица 2
| 21,3; | 26,4; | 29,2; | 30,7; | 31,3; | 31,9 | 31,9; | 33,0; |
| 33,2; | 33,7; | 33,8; | 36,0; | 37,0; | 37,5 | 37,6; | 37,6; |
| 38,0; | 39,6; | 40,0; | 40,4; | 42,1; | 42,6 | 42,7; | 42,7; |
| 43,6; | 43,8; | 43,9; | 44,0; | 44,4; | 44,6 | 44,7; | 45,1; |
| 45,1; | 45,3; | 45,5; | 45,5; | 45,9; | 46,0 | 46,2; | 47,4; |
| 47,5; | 48,5; | 48,6; | 49,0; | 49,7; | 50,7 | 50,9; | 51,5; |
| 52,1; | 52,2; | 53,3; | 53,7; | 55,4; | 57,7 | 58,9; | 59,2; |
| 59,4; | 59,6; | 60,6; | 64,6. |
![]() .
.
Определим шаг или длину интервала, по формуле Стерджесса
![]() , (1)
, (1)
![]() .
.
Таблица 3
|
|
|
|
|
|
| [18; 25) | 21,5 | 1 | 0,0167 | 0,0024 |
| [25; 32) | 28,5 | 6 | 0,1 | 0,0142 |
| [32; 39) | 35,5 | 10 | 0,1667 | 0,0238 |
| [39; 46) | 42,5 | 20 | 0,3333 | 0,0476 |
| [46; 53) | 49,5 | 13 | 0,2167 | 0,0309 |
| [53; 60) | 56,5 | 8 | 0,1333 | 0,0190 |
| [60; 67) | 63,5 | 2 | 0,0333 | 0,0048 |
|
| 60 | 1 |
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() - частота;
- частота;
![]() - относительная частота;
- относительная частота;
![]() - плотности относительных частот.
- плотности относительных частот.
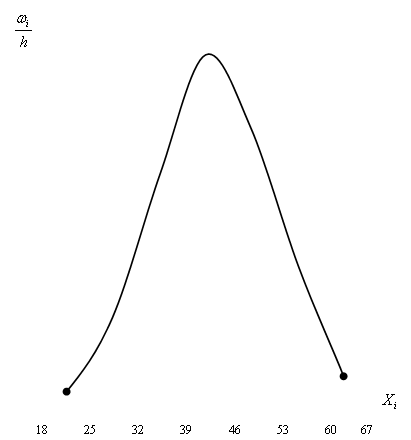
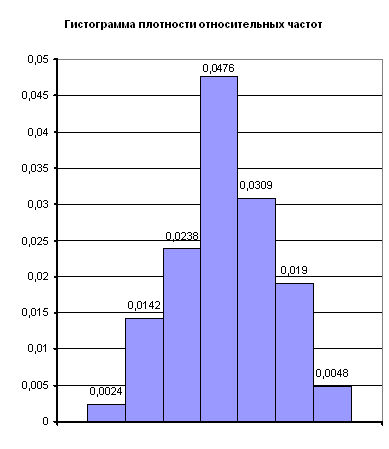
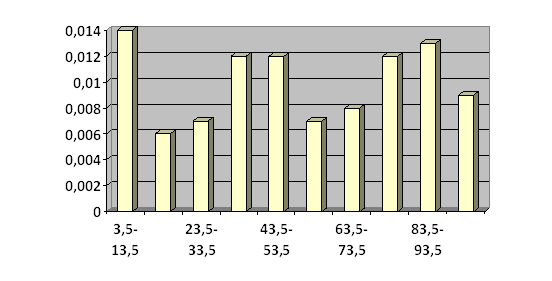
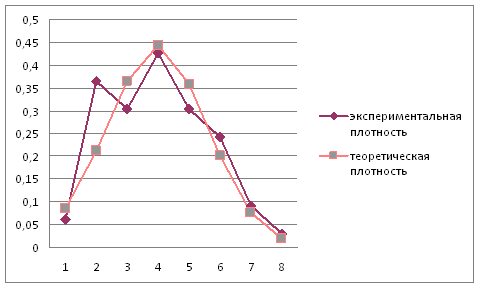
Рис. 1. Гистограмма плотности относительных частот
По построенной гистограмме (рис.1) можно предположить, что данное распределение подчиняется нормальному закону. Для подтверждения выдвинутой гипотезы проведем оценку неизвестных параметров, для мат. Ожидания
![]() , (2)
, (2)
![]() .
.
для несмещенной оценки дисперсии
![]() , (3)
, (3)
![]()
Функция плотности имеет вид
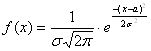 , (4)
, (4)
где ![]() ,
,
![]() .
.
Пользуясь приложением 3 в учебнике Вентцель Е.С. - "Теория вероятностей" - М.: Высшая школа, 1998., получим значения ![]()
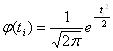 (5)
(5)
![]() (6)
(6)
![]()
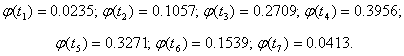
![]()
![]() . (7)
. (7)
Полученные значения занесем в таблицу 4
Таблица 4
|
|
|
| 21.5 | 0.0025 |
| 28.5 | 0.0114 |
| 35.5 | 0.0291 |
| 42.5 | 0.0425 |
| 49.5 | 0.0351 |
| 56.5 | 0.0165 |
| 63.5 | 0.0044 |
Найду соответствующие вероятности для каждого разряда
Из ТВ для нормальной случайной величины ![]()
![]() (8)
(8)
Значения функции Лапласа, находим в приложении 2, учебника Вентцель Е.С., Овчаров Л.А., теория вероятностей и её инженерные приложения. Учеб. пособие для вузов. - 2-е изд., стер. - М.: Высш. шк., 2000.
![]()
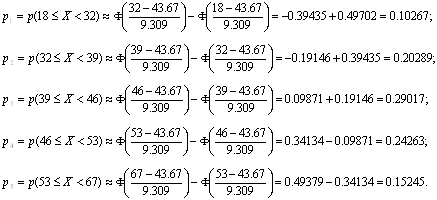
Таблица 5
|
|
|
|
|
| |
|
| 7 | 10 | 20 | 13 | 10 |
|
| 0,12567 | 0, 20289 | 0,29017 | 0,24263 | 0,15245 |
|
| 7,5402 | 12,1734 | 17,4102 | 14,5578 | 9,1470 |
|
| -0,5402 | -2,1734 | 2,5898 | -1,5578 | 0,8530 |
|
| 0,2918 | 4,7237 | 6,7071 | 2,4267 | 0,7276 |
|
| 0,0387 | 0,3880 | 0,3852 | 0,1667 | 0,079 |
![]() . (9)
. (9)
![]() - расчетное
- расчетное
Найдем число степеней свобод
![]() (10)
(10)
Где k=5; s=3;
r=2
Для ![]()
Получили:
![]() .
.
Гипотеза о нормальном распределении генеральной совокупности, из которой сформирована выборка, не противоречит экспериментальным данным.
4. Нахождение доверительного интервала4.1 Оценка математического ожидания ![]()
4.2 Оценка дисперсии ![]() .
.
4.3 Среднеквадратичное отклонение оценки
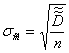 , (11)
, (11)
![]() .
.
4.4 По функции Лапласа, определим t
![]() ;
;
![]() (12)
(12)
где![]()
![]() .
.
4.5 Точность оценки
![]() (13)
(13)
![]()
4.6 Доверительный интервал ![]()
![]()
При достаточно большом числе выборок, ![]() из них имеет такие доверительные интервалы. А в 5% оценив параметры математического может выходить за пределы доверительного интервала.
из них имеет такие доверительные интервалы. А в 5% оценив параметры математического может выходить за пределы доверительного интервала.
Похожие работы
... После того, как найдены значения функции плотности для каждого разряда, нанесем их прямо на гистограмму, получая тем самым кривую функции плотности 7 Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона В качестве меры расхождения между статистическим и гипотетическим (теоретическим) распределениями возьмем критерий Пирсона К = ч2. Пирсон доказал, что ...
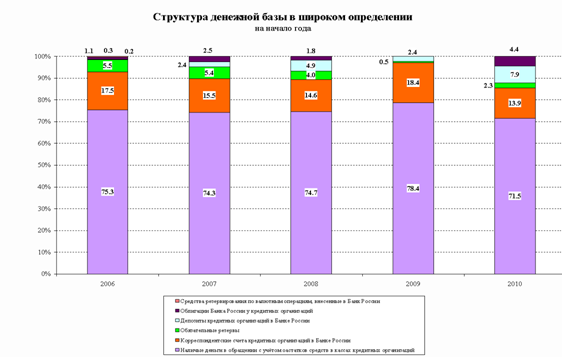
... денежными системами и нередко заимствуя их отдельные элементы, российское денежное хозяйство всегда сохраняло определенное своеобразие, связанное с особенностями и потребностями народного хозяйства страны. [2] Предметом изучения статистики денежного обращения является количественная характеристика массовых явлений в сфере денежного обращения. Денежное обращение - это движение денег во внутреннем ...
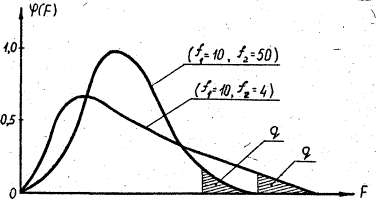
... дисперсию, то при условии однородности оценок дисперсий целесообразно принять в качестве ее оценки среднее арифметическое несмещенных оценок дисперсий 1.9. Критерий Пирсона Нормальный закон распределения характеризуется плотностью вероятности вида где M{X}, ____ — соответственно математическое ожидание и дисперсия случайной величины. согласованности изучаемого распределения с ...
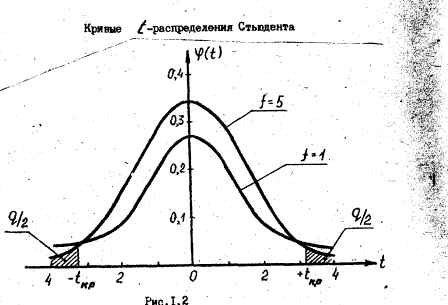
... Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы Цель математической обработки результатов эксперимента; Виды измерений; Типы ошибок измерения; Свойства случайных ошибок; Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является ...
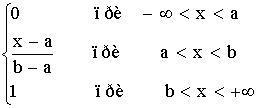
0 комментариев