Навигация
Проектный и проверочный расчёт зубчатых передач
5. Проектный и проверочный расчёт зубчатых передач
Расчёт тихоходной ступени редуктора.Материал колеса и шестерни – сталь 45 улучшение. Таким образом, учитывая, что термообработка зубчатых колёс – улучшение, по таблице 3.1 имеем:
для шестерни: ![]() ,
, ![]() ,
, ![]() ;
;
для колеса: ![]() ,
, ![]() ,
, ![]() ;
;
где ![]() – твёрдость рабочей поверхности зубьев,
– твёрдость рабочей поверхности зубьев, ![]() и
и ![]() – предел прочности материала на растяжение и предел текучести материала.
– предел прочности материала на растяжение и предел текучести материала.
Определим коэффициенты приведения на контактную выносливость ![]() и на изгибную выносливость
и на изгибную выносливость ![]() по таблице 4.1 лит. 1, учитывая режим работы №0:
по таблице 4.1 лит. 1, учитывая режим работы №0: ![]() ;
; ![]() .
.
Определим число циклов перемены напряжений. Числа циклов ![]() перемены напряжений соответствуют длительному пределу выносливости. По графику 4.3 определяем числа циклов на контактную и изгибную выносливость соответственно:
перемены напряжений соответствуют длительному пределу выносливости. По графику 4.3 определяем числа циклов на контактную и изгибную выносливость соответственно: ![]() ,
, ![]() ,
, ![]() .
.
Определим суммарное число циклов перемены напряжений для шестерни и колеса соответственно: ![]()
![]() , где
, где ![]() и
и ![]() – частота вращения шестерни и колеса соответственно;
– частота вращения шестерни и колеса соответственно; ![]() – число вхождений в зацепление зубьев шестерни или колеса соответственно за один его оборот.
– число вхождений в зацепление зубьев шестерни или колеса соответственно за один его оборот.
Так как ![]() , то принимаем
, то принимаем ![]() .
.
Так как ![]() , то принимаем
, то принимаем ![]() .
.
Найдём эквивалентное число циклов перемены напряжений для расчёта на изгибную выносливость: ![]() ,
, ![]() , где
, где ![]() – коэффициенты приведения на изгибную выносливость;
– коэффициенты приведения на изгибную выносливость; ![]() – суммарное число циклов перемены напряжений для шестерни или колеса.
– суммарное число циклов перемены напряжений для шестерни или колеса.
Так как ![]() , то принимаем
, то принимаем ![]() .
.
Так как ![]() , то принимаем
, то принимаем ![]() .
.
Определим допускаемые напряжения для расчётов на выносливость. По таблице 4.3 находим, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() – для шестерни и
– для шестерни и ![]() ,
, ![]() ,
, ![]() ,
, ![]() – для зубчатого колеса,
– для зубчатого колеса,
где ![]() и
и ![]() – длительный предел контактной выносливости и коэффициент безопасности;
– длительный предел контактной выносливости и коэффициент безопасности; ![]() и
и ![]() – длительный предел изгибной выносливости и коэффициент безопасности; Найдём предельные допускаемые контактные и изгибные напряжения:
– длительный предел изгибной выносливости и коэффициент безопасности; Найдём предельные допускаемые контактные и изгибные напряжения: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() – предел текучести материала колеса или шестерни;
– предел текучести материала колеса или шестерни;
Определим допускаемые контактные напряжения и напряжения изгиба при неограниченном ресурсе передачи:  ,
,  ,
, 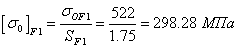 ,
,  , где
, где ![]() и
и ![]() – длительный предел контактной выносливости и коэффициент безопасности;
– длительный предел контактной выносливости и коэффициент безопасности; ![]() и
и ![]() – длительный предел изгибной выносливости и коэффициент безопасности.
– длительный предел изгибной выносливости и коэффициент безопасности.
Проверим передачу на контактную выносливость и изгибную выносливость:  ,
, 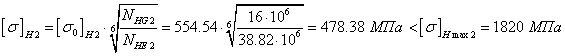 ,
, 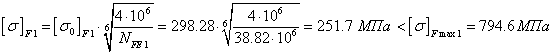 ,
,  .
.
Выбираем допускаемое контактное напряжение как меньшее из значений: ![]() .
.
![]()
Принимаем ![]()
Определим предварительное значение межосевого расстояния:
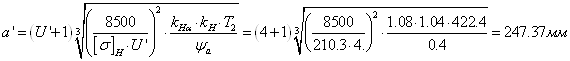
где ψа = 0,4 – коэффициент ширины тихоходной ступени.
![]() =4– передаточное число ступени редуктора;
=4– передаточное число ступени редуктора;
![]() = 210.3 МПа – допускаемое контактное напряжение;
= 210.3 МПа – допускаемое контактное напряжение;
![]() =1.04 – коэффициент, учитывающий распределение нагрузки между зубьями, определяем по рис. 6.2;
=1.04 – коэффициент, учитывающий распределение нагрузки между зубьями, определяем по рис. 6.2;
![]() =422.4Н м– крутящий момент на валу колеса;
=422.4Н м– крутящий момент на валу колеса;
![]() – коэффициент нагрузки на контактную выносливость, определяется следующим образом.
– коэффициент нагрузки на контактную выносливость, определяется следующим образом.
Найдём коэффициенты нагрузки на контактную и изгибную выносливость по формулам:
![]() и
и ![]() ,
,
где ![]() и
и ![]() – коэффициенты концентрации нагрузки по ширине зубчатого венца;
– коэффициенты концентрации нагрузки по ширине зубчатого венца;
![]() и
и ![]() – коэффициенты динамической нагрузки (учитывают внутреннюю динамику передачи).
– коэффициенты динамической нагрузки (учитывают внутреннюю динамику передачи).
![]() - для прирабатывающихся зубьев при постоянной нагрузке;
- для прирабатывающихся зубьев при постоянной нагрузке;
Коэффициент ![]() определяется по табл. 5.4 в зависимости от вида передачи (в данном случае цилиндрическая косозубая). Находим, что
определяется по табл. 5.4 в зависимости от вида передачи (в данном случае цилиндрическая косозубая). Находим, что ![]() и
и ![]() . Теперь находим значения коэффициентов нагрузки
. Теперь находим значения коэффициентов нагрузки
![]() и
и ![]() .
.
Принимаем а = 250 мм
Определяем рабочую ширину колеса:
![]() .
.
Ширина шестерни: ![]() .
.
Вычислим модуль передачи по формуле:
 ,где
,где ![]() =215.7МПа–изгибное напряжение на колесе;
=215.7МПа–изгибное напряжение на колесе; ,
, 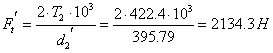 . Тогда
. Тогда  . Из стандартного ряда значений
. Из стандартного ряда значений ![]() по ГОСТ 9563–60 выбираем значение
по ГОСТ 9563–60 выбираем значение ![]() .
.
Определим минимально возможный угол наклона зуба ![]() .
.
Рассчитываем предварительное суммарное число зубьев: ![]() . Округляем это число и получаем
. Округляем это число и получаем ![]() .
.
Определяем действительное значение угла ![]() и сравниваем его с минимальным значением:
и сравниваем его с минимальным значением:
![]() .
.
Найдём число зубьев шестерни ![]() и колеса
и колеса ![]() , учитывая что минимальное число зубьев для косозубой цилиндрической передачи
, учитывая что минимальное число зубьев для косозубой цилиндрической передачи ![]() ;
; ![]() .
.
Найдём фактическое передаточное число передачи: ![]() . Таким образом отклонение фактического передаточного числа данной ступени редуктора от номинального значения
. Таким образом отклонение фактического передаточного числа данной ступени редуктора от номинального значения ![]() .
.
Проверим зубья колёс на изгибную выносливость. Для колеса получим:![]() где
где ![]() – коэффициент нагрузки при расчёте на изгибную выносливость;
– коэффициент нагрузки при расчёте на изгибную выносливость;
![]() – коэффициент, учитывающий распределение нагрузки между зубьями, выбираем по табл. 6.4;
– коэффициент, учитывающий распределение нагрузки между зубьями, выбираем по табл. 6.4;
![]() – коэффициент, учитывающий форму зуба, находится по табл. 6.2 лит. 1;
– коэффициент, учитывающий форму зуба, находится по табл. 6.2 лит. 1;
![]() – коэффициент, учитывающий наклон зуба.
– коэффициент, учитывающий наклон зуба.
Сравниваем полученное значение напряжения с допускаемым напряжением при расчёте на изгиб зубьев колеса: ![]() .
.
Для шестерни:  ,
,
где ![]() и
и ![]() – коэффициенты, учитывающие форму зуба, определяются по табл. 6.2.
– коэффициенты, учитывающие форму зуба, определяются по табл. 6.2.
Сравним полученное значение напряжения с допускаемым напряжением при расчёте на изгиб зубьев шестерни: ![]() .
.
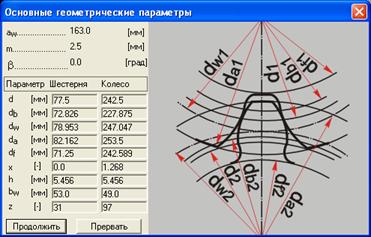
Определим диаметры делительных окружностей шестерни и колеса соответственно.
![]() ,
, ![]() ,
,
где ![]() – модуль зубчатых колёс;
– модуль зубчатых колёс;
![]() – угол наклона зуба;
– угол наклона зуба;
Вычислим диаметры окружностей вершин зубьев ![]() и впадин зубьев
и впадин зубьев ![]() .
.
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Материал колеса и шестерни – сталь 45. Таким образом, учитывая, что термообработка зубчатых колёс и шестерни – улучшение, имеем:
для шестерни:, ![]() ;
;
для колеса:, ![]() ;
;
где ![]() – твёрдость рабочей поверхности зубьев,
– твёрдость рабочей поверхности зубьев, ![]() – предел текучести материала.
– предел текучести материала.
Определим твёрдость зубьев шестерни и колеса:
![]() ;
;
![]() .
.
Определим коэффициенты приведения на контактную выносливость ![]() и на изгибную выносливость
и на изгибную выносливость ![]() по таблице 4.1., учитывая режим работы №3:
по таблице 4.1., учитывая режим работы №3: ![]() ;
; ![]() .
.
Определим число циклов перемены напряжений.
Определим суммарное число циклов перемены напряжений для шестерни и колеса соответственно:
![]() ,
, ![]() ,
,
где ![]() –ресурс передачи;
–ресурс передачи; ![]() и
и ![]() – частота вращения шестерни и колеса соответственно;
– частота вращения шестерни и колеса соответственно; ![]() =
=![]() =1 – число вхождений в зацепление зубьев шестерни или колеса соответственно за один его оборот.
=1 – число вхождений в зацепление зубьев шестерни или колеса соответственно за один его оборот.
Числа циклов ![]() перемены напряжений соответствуют длительному пределу выносливости. По графику 4.3. определяем числа циклов на контактную и изгибную выносливость соответственно:
перемены напряжений соответствуют длительному пределу выносливости. По графику 4.3. определяем числа циклов на контактную и изгибную выносливость соответственно:
![]() ,
, ![]() ,
, ![]() .
.
Определим эквивалентное число циклов перемены напряжений для расчёта на контактную выносливость:
![]()
![]() ,
,
где ![]() – коэффициенты приведения на контактную выносливость;
– коэффициенты приведения на контактную выносливость; ![]() – суммарное число циклов перемены напряжений для шестерни или колеса.
– суммарное число циклов перемены напряжений для шестерни или колеса.
Так как ![]() , то принимаем
, то принимаем ![]() и
и ![]() , то
, то
![]() .
.
Определим эквивалентное число циклов перемены напряжений для расчёта на изгибную выносливость:
![]() ,
,
![]() ,
,
где ![]() – коэффициенты приведения на изгибную выносливость;
– коэффициенты приведения на изгибную выносливость; ![]() – суммарное число циклов перемены напряжений для шестерни или колеса.
– суммарное число циклов перемены напряжений для шестерни или колеса.
Так как ![]() и
и ![]() , то принимаем
, то принимаем ![]() .
.
Определим допускаемые напряжения для расчётов на выносливость. По таблице 4.3 находим
для шестерни:
![]() ,
,
![]()
![]() ,
, ![]()
для зубчатого колеса:
![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,
где ![]() и
и ![]() – длительный предел контактной выносливости и коэффициент безопасности;
– длительный предел контактной выносливости и коэффициент безопасности; ![]() и
и ![]() – длительный предел изгибной выносливости и коэффициент безопасности;
– длительный предел изгибной выносливости и коэффициент безопасности; ![]() – твёрдость зубьев шестерни или колеса.
– твёрдость зубьев шестерни или колеса.
Определим предельные допускаемые контактные и изгибные напряжения:
![]() ,
,
![]()
![]() ,
,
![]()
где ![]() – предел текучести материала колеса или шестерни;
– предел текучести материала колеса или шестерни; ![]() –твёрдость зубьев шестерни или колеса.
–твёрдость зубьев шестерни или колеса.
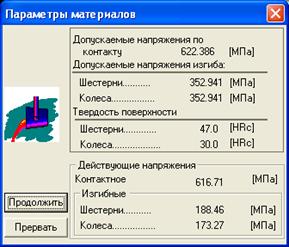
Проверим передачу на контактную выносливость:
 ,
, 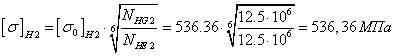 ,
,  ,
,  .
.
Принимаем допускаемое контактное напряжение как меньшее значение:
![]()
![]()
![]() .
.
Определим коэффициенты нагрузки на контактную и изгибную выносливость по формулам:
![]() и
и ![]() ,
,
где ![]() и
и ![]() – коэффициенты концентрации нагрузки по ширине зубчатого венца;
– коэффициенты концентрации нагрузки по ширине зубчатого венца; ![]() и
и ![]() – коэффициенты динамической нагрузки (учитывают внутреннюю динамику передачи).
– коэффициенты динамической нагрузки (учитывают внутреннюю динамику передачи).
Относительная ширина зубчатого венца находится по формуле
![]() ,
,
![]() =4.5 – передаточное число данной ступени редуктора.
=4.5 – передаточное число данной ступени редуктора.
По таблице 5.2. и 5.3, схемы 2 расположения зубчатых колёс относительно опор и варианта соотношения термических обработок “a” находим ![]() ,
, ![]()
Тогда
![]()
![]()
Значения ![]() определяются по табл. 5.6
определяются по табл. 5.6
Коэффициент ![]() определяется по табл. 5.4 в зависимости от вида передачи.
определяется по табл. 5.4 в зависимости от вида передачи.
Принимаем 8-ю степень точности изготовления передачи находим, что
![]() и
и ![]() .
.
Теперь находим значения коэффициентов нагрузки
![]()
![]()
Определим коэффициент ширины быстроходной ступени ![]()
![]()
Определяем рабочую ширину колеса:
![]() .
.
Ширина шестерни: ![]() .
.
Вычислим модуль передачи по формуле:
 ,
,
где ![]() =257.1 МПа – изгибное напряжение на колесе;
=257.1 МПа – изгибное напряжение на колесе;  ,
,  . Тогда
. Тогда  . Из стандартного ряда значений
. Из стандартного ряда значений ![]() по ГОСТ 9563–60 выбираем значение
по ГОСТ 9563–60 выбираем значение ![]() .
.
Определим минимально возможный угол наклона зуба ![]() .
.
Рассчитываем предварительное суммарное число зубьев: ![]() . Округляем это число и получаем
. Округляем это число и получаем ![]() .
.
Определяем действительное значение угла ![]() и сравниваем его с минимальным значением:
и сравниваем его с минимальным значением:
![]() .
.
Найдём число зубьев шестерни ![]() и колеса
и колеса ![]() , учитывая, что минимальное число зубьев для косозубой цилиндрической передачи
, учитывая, что минимальное число зубьев для косозубой цилиндрической передачи ![]() ;
; ![]() .
.
Найдём фактическое передаточное число передачи: ![]() . Таким, образом отклонение фактического передаточного числа данной ступени редуктора от номинального значения
. Таким, образом отклонение фактического передаточного числа данной ступени редуктора от номинального значения ![]() .
.
Проверим зубья колёс на изгибную выносливость. Для колеса получим:![]() где
где ![]() – коэффициент нагрузки при расчёте на изгибную выносливость;
– коэффициент нагрузки при расчёте на изгибную выносливость;
![]() – коэффициент, учитывающий распределение нагрузки между зубьями, выбираем по табл. 6.4;
– коэффициент, учитывающий распределение нагрузки между зубьями, выбираем по табл. 6.4;
![]() – коэффициент, учитывающий форму зуба, находится по табл. 6.2 лит. 1;
– коэффициент, учитывающий форму зуба, находится по табл. 6.2 лит. 1;
![]() – коэффициент, учитывающий наклон зуба.
– коэффициент, учитывающий наклон зуба.
Сравниваем полученное значение напряжения с допускаемым напряжением при расчёте на изгиб зубьев колеса: ![]() .
.
Определим диаметры делительных окружностей шестерни и колеса соответственно.
![]() ,
, ![]() ,
,
где ![]() – модуль зубчатых колёс;
– модуль зубчатых колёс;
![]() – угол наклона зуба;
– угол наклона зуба;
Проверка
Вычислим диаметры окружностей вершин зубьев ![]() и впадин зубьев
и впадин зубьев ![]()
![]() ;
;![]() ;
; ![]() ;
; ![]() .
.
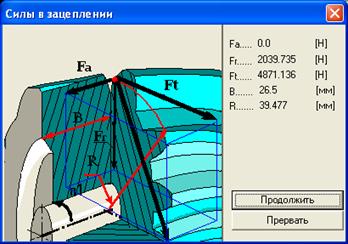
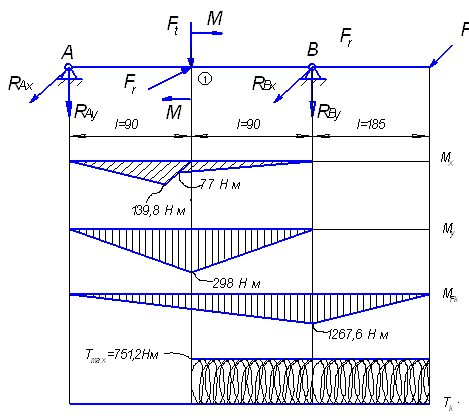
Определим силы, действующие на валы зубчатых колёс.
Окружную силу на среднем находим по формуле:
![]() Н,
Н,
Осевая сила на шестерне:
![]() Н,
Н,
Радиальная сила на шестерне:
![]() Н
Н
Определим диаметр быстроходного вала шестерни: ![]() , где
, где ![]() – момент на быстроходном валу. Примем
– момент на быстроходном валу. Примем ![]() . Сравним этот диаметр с диаметром вала электродвигателя, при этом должно выполняться условие
. Сравним этот диаметр с диаметром вала электродвигателя, при этом должно выполняться условие ![]() – условие выполняется.
– условие выполняется.
Определим диаметр посадочной поверхности подшипника:![]() . Примем dк = 30мм. Диаметр вала под колесо
. Примем dк = 30мм. Диаметр вала под колесо ![]() . Рассчитаем диаметр буртика для упора подшипника:
. Рассчитаем диаметр буртика для упора подшипника: ![]() . Примем d бк = 32мм.
. Примем d бк = 32мм.
Определим диаметры промежуточного вала: ![]() , где Т2 – момент на промежуточном валу. Примем dк = 35 мм. Для найденного диаметра вала выбираем значения:
, где Т2 – момент на промежуточном валу. Примем dк = 35 мм. Для найденного диаметра вала выбираем значения: ![]() – приблизительная высота буртика,
– приблизительная высота буртика, ![]() – максимальный радиус фаски подшипника,
– максимальный радиус фаски подшипника, ![]() – размер фасок вала. Диаметр вала под колесо
– размер фасок вала. Диаметр вала под колесо ![]() . Примем диаметр dк =38. Диаметр буртика для упора колеса
. Примем диаметр dк =38. Диаметр буртика для упора колеса ![]() . Принимаем dбк = 42мм.
. Принимаем dбк = 42мм.
Определим диаметр тихоходного вала: ![]() , где
, где ![]() – момент на тихоходном валу. Примем
– момент на тихоходном валу. Примем ![]() . Для найденного диаметра вала выбираем значения:
. Для найденного диаметра вала выбираем значения: ![]() – приблизительная высота буртика,
– приблизительная высота буртика, ![]() – максимальный радиус фаски подшипника,
– максимальный радиус фаски подшипника, ![]() – размер фасок вала. Определим диаметр посадочной поверхности подшипника:
– размер фасок вала. Определим диаметр посадочной поверхности подшипника: ![]() . Так как стандартные подшипники имеют посадочный диаметр, кратный
. Так как стандартные подшипники имеют посадочный диаметр, кратный ![]() -ти, то принимаем
-ти, то принимаем ![]() . Рассчитаем диаметр буртика для упора подшипника:
. Рассчитаем диаметр буртика для упора подшипника: ![]() . Пусть
. Пусть ![]() .
.
Похожие работы
... частот вращения валов привода Номинальные частоты вращения валов в заданном приводе определяют с учётом выполненной разбивки общего передаточного отношения по ступеням передаточного механизма привода. Частота вращения вала 1 (входного вала редуктора): n1 = nД, (1.8) n1 = 700 мин-1. Частота вращения вала 2 (промежуточного вала привода): , ...
расчете учитываем к.п.д. привода, частоту вращения, мощность двигателя, крутящий момент на тихоходном валу. В зависимости крутящего момента и диаметра вала из справочника выбираем подходящую муфту. Для дальнейшей разработки и изготовления редуктора необходимо наглядное представление о нем. Для этого чертятся чертежи, по которым можно точно определить месторасположения каждой детали. По ...
... М1 и М2; =0,99 - коэффициент полезного действия подшипников. Частота вращения на валах определяется по формулам: Где - частоты вращения на I, II, III валах привода, об/мин =1430 об/мин - частоты вращения вала электродвигателя; - передаточное отношение редуктора. Момент на валах определяется по формулам: где - моменты на I, II, III валах , Нм Номер вала P, кВт n, об/мин Т, ...
7,2*0,98= =7,05 кВт n3=n2/Uпр=151/4,4= =34 мин - 1 Т3=9550*Р3/n3=9550*7,05/34=1980 Нм Р4=Р3*nт=7,05*0,98=6,91 n4= n3 =34 мин - 1 Т4=9550*Р4/n4=9550*6,91/34=1940 Нм 1.4 Выбор материала и определение допускаемых напряжений быстроходной ступени Таблица 2. Колесо Z2 Шестерня Z1 Сталь 40Х улучшение НВ2=269…302 НВ2ср=285 σT = 750 МПа ...
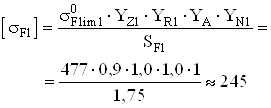
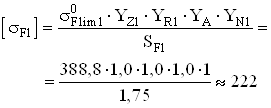

0 комментариев