Навигация
372 МПа < 511 МПа < 639 МПа
Расчет размеров прямозубой передачи
Кн = 1.4 – коэффициент нагрузки
- коэффициент зубчатого колеса
Ка = 450
Межосевое расстояние:
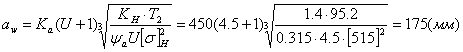
aW принимаем = 160 (мм) из числа стандартных длин
Выбираем нормальный модуль
, принимаем m = 2.
Определяем количество зубьев на шестерне и колесе
; 
.
Определяем делительный диаметр
; 
,
Диаметр выступов
; 
Диаметры впадин
; 
Ширина колеса
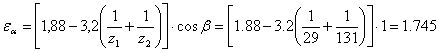
Окружная скорость
Проверочный расчет
Коэффициенты нагрузки
Где 
коэффициенты внутренней динамической нагрузки
коэффициенты концентрирования напряжения
коэффициенты распределения нагрузки между зубьями
Проверка по контактным напряжениям
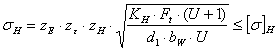
коэффициент металла для стали = 190
коэффициент учета сумарной длины контактных линий = 2,5
Расчет размеров косозубой передачи
Кн = 1.3 – коэффициент нагрузки
- коэффициент зубчатого колеса
Ка = 410
Межосевое расстояние:
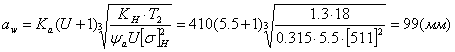
aW принимаем = 100 из числа стандартных длин
Выбираем нормальный модуль
, принимаем m = 1.25
Определяем количество зубьев на шестерне и колесе
; 
.
Принимаем количество зубьев z1 = 30, z2 = 165
Определяем делительный диаметр
; 
Диаметр выступов
; 
Диаметры впадин
; 
Ширина колеса
; 
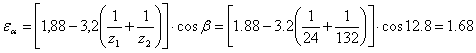
Окружная скорость
Проверочный расчет
Коэффициенты нагрузки
Где коэффициенты внутренней динамической нагрузки
коэффициенты концентрирования напряжения
коэффициенты распределения нагрузки между зубьями
Проверка по контактным напряжениям
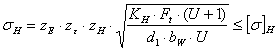
коэффициент металла для стали = 190
коэффициент учета суммарной длины контактных линий = 2,42
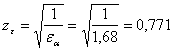
Проверка по усталостным напряжениям изгиба
Допускаемое напряжение изгиба для косозубой передачи
YR = 1 – коэффициент шероховатости
YA = 1
принимаем = 1.
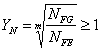, m =6 – для улучшенных сталей, m = 9 – для закаленных сталей.
- число циклов
берем 
; 
берем 
; 
Для шестерни
Для колеса
Допускаемое напряжение изгиба для прямозубой передачи
YR = 1 – коэффициент шероховатости
YA = 1
принимаем = 1.
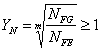, m =6 – для улучшенных сталей, m = 9 – для закаленных сталей.
- число циклов
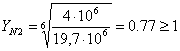берем ; 
берем ; 
Для шестерни
Для колеса
Рабочие напряжения изгиба для колеса прямозубой передачи
-коэффициент формы зуба
– коэффициент перекрытия зубьев в зацеплении
– коэффициент угла наклона
; 
; b = 50,4 мм; m = 2;
Проверка на контактную статическую прочность
Проверка изгибной статической прочности
Рабочие напряжения изгиба для шестерни прямозубой передачи
-коэффициент формы зуба
– коэффициент перекрытия зубьев в зацеплении
– коэффициент угла наклона
; ; b = 50,4 мм; m = 2;
Проверка на контактную статическую прочность
Проверка изгибной статической прочности
Рабочие напряжения изгиба для колеса косозубой передачи
-коэффициент формы зуба
– коэффициент перекрытия зубьев в зацеплении
– коэффициент угла наклона
; 
; b = 31,5 мм; m =1.25; х=0
Проверка на контактную статическую прочность
Проверка изгибной статической прочности
Рабочие напряжения изгиба для шестерни косозубой передачи
-коэффициент формы зуба
– коэффициент перекрытия зубьев в зацеплении
– коэффициент угла наклона
; ; b = 31,5 мм; m =1.25; х=0
Проверка на контактную статическую прочность
Проверка изгибной статической прочности
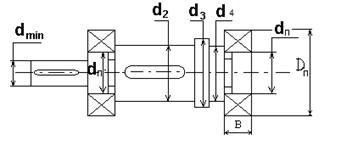
Ориентировочный расчет валов
Диаметр вала определим в зависимости от крутящего момента и напряжений вала при кручении
Для быстроходного вала:
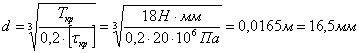
Выбираем диаметр вала d=22 мм
Для промежуточного вала:
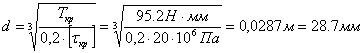
Выбираем диаметр вала d=30 мм
Для тихоходного вала:
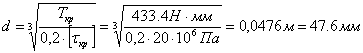
Выбираем диаметр вала d=50 мм
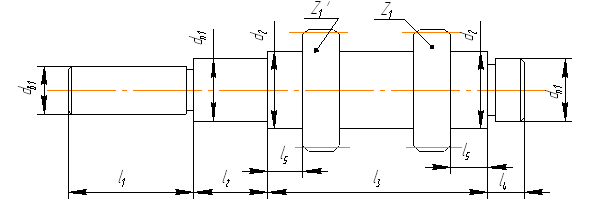
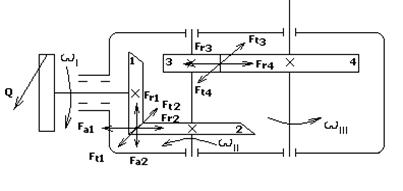
Расчет валов
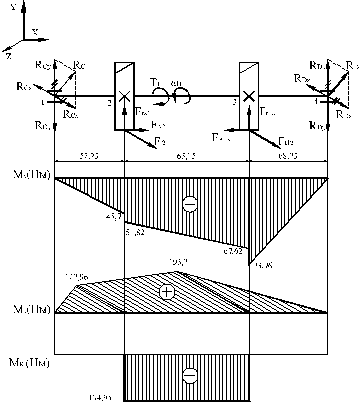
Быстроходный вал
окружное усилие на шестерне
Осевая сила на шестерне
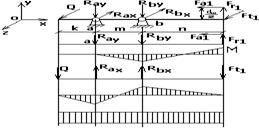
В плоскости ZoY
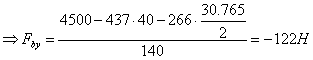
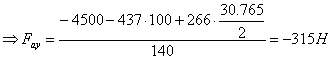В плоскости XoY
В т. С 
В т. А 
В т. D 
В т. D 
В т. B 
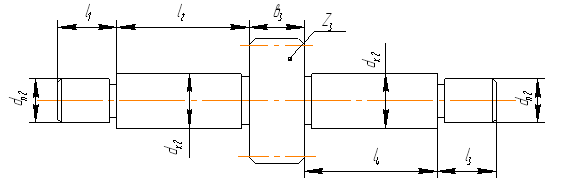
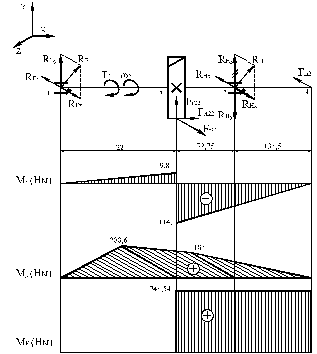
Промежуточный вал
окружное усилие на колесе
Окружное усилие на шестерне
Осевая сила на колесе
В плоскости ZoY
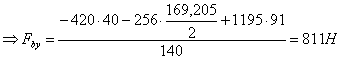
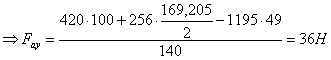
В плоскости XoY
;
;
;
;
;
;
;
;
;
В т. С 
В т. А 
В т. B
В т. D 
В т. С 
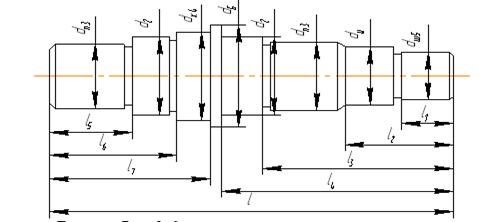
Тихоходный вал
окружное усилие на шестерне
В плоскости ZoY
В плоскости XoY
В т. С 
В т. А 
В т. D 
В т. B
Расчёт подшипников
Быстроходный вал в точке А
d=25; D=62; B=17; C=22500; C0=11400
; 
;
;
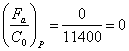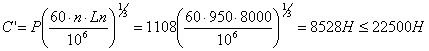Быстроходный вал в точке B
d=25; D=52; B=15; C=14000; C0=6950
; 
;
;
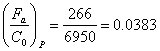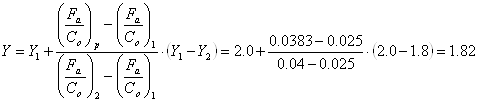
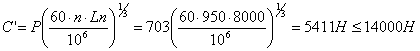Промежуточный вал в точке А
d=30; D=62; B=16; C=19500; C0=10000
; 
;
;
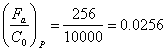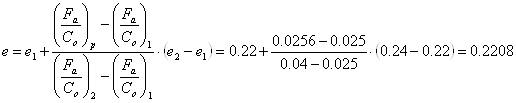
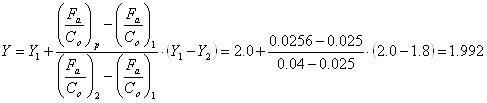
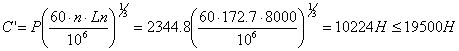Промежуточный вал в точке В
d=30; D=62; B=16; C=19500; C0=10000
; 
;
;
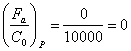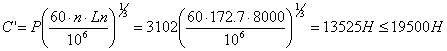Тихоходный вал в точке А
d=50; D=90; B=20; C=35100; C0=19800
; 
;
;
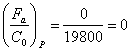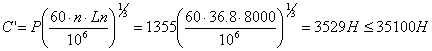Тихоходный вал в точке В
d=50; D=90; B=20; C=35100; C0=19800
; 
;
;
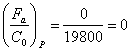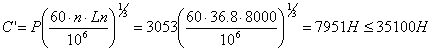
Похожие работы
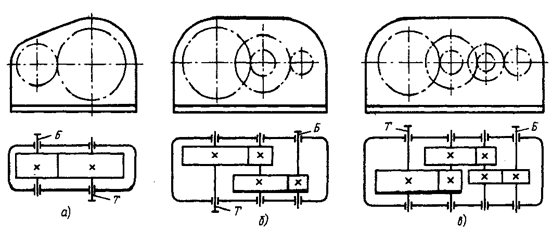
... при проектировании машины, т.е. соответствия этого выбора действующей нормативной документации (НД). 3. Построение компоновки цилиндрического двухступенчатого редуктора Задачей курсовой работы является построение и параметризация компоновочного чертежа многоступенчатого редуктора, поэтому кинематические расчеты производиться не будут и за основу взята модель ранее спроектированного редуктора. ...
... a2= m(z1+z2)/2= 0,3(24+49)/2= 10,95 a3= m(z1+z2)/2= 0,3(24+54)/2= 11,7 a4= m(z1+z2)/2= 0,3(24+55)/2= 11,85 a5= m(z1+z2)/2= 0,3(24+68)/2= 13,8 Определим ширину венца: b= (3…15)m= 10·0,3= 3 Определим высоту зуба: h= 2,5m= 2,5·0,3= 0,75 5. Разработка конструкций редуктора Разработка конструкции состоит в расчете и выборе его элементов: зубчатые колеса, валы, подшипники и корпуса. ...
... 405,6 Напряжение на изгиб σF, Н/мм2 114,7 110,7 Межосевое расстояние аw, мм 240 Угол наклона зубьев b, ° 10,14 Фактическое передаточное число редуктора uф 4,56 Модуль передачи m 2,5 3.3. Расчет нагрузок привода Силы в зацеплении первой ступени Определим окружную силу. , (34) Н Определим радиальную силу. , ...
... w и Т заносятся в таблицу 3.1. Примечание. Для одноступенчатого редуктора крутящий момент определяется по формуле , [Н·м]; , [Н·м]; [Н·м]; , [Н·м]. [Н·м]. Расчет клиноременной передачи Расчет клиноременной передачи проводим исходя из ранее рассчитанной мощности электродвигателя, Рэд и принятого передаточного отношения клиноременной передачи iр.п.=2. Определение сечения ремня ...
0 комментариев