Параметрическая оптимизация

3 Параметрическая оптимизация

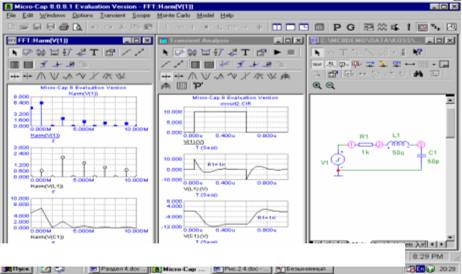
Параметрическая оптимизация выполняется в программе МС7 методом Пауэлла (Powell) в любом из видов анализа: анализ переходных процессов, малосигнальный АС-анализ и расчет характеристик на постоянном токе DC. Проиллюстрируем последовательность действий при оптимизации на примере схемы OPT4.CIR из каталога ANALYSIS\OPTIMIZE, изображенной на рис. 3. Задача приведенного примера состоит в том, чтобы изменяя параметры схемы R1, C1, L1 в процессе проведения оптимизации добиться максимально близкого расположения амплитудно-частотной характеристики к 6 заданным точкам (частота, амплитуда).

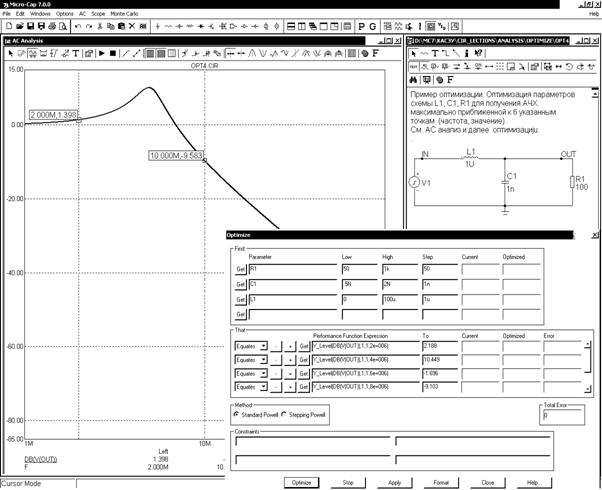
Рис. 3. Пример оптимизации схемы Opt4.cir

Сначала в меню Analysis выберем режим АС и нажмем на клавишу Run (F2) и затем на клавишу F8, чтобы вывести маркеры для считывания с графиков численных значений (рис. 3). Заметим, что на частотах 2 и 10 МГц переменная db(V(Out)) равна 1,398 и -9,583 дБ соответственно.

После этого нажатием на кнопку  (Ctrl+F11) открывают диалоговое окно, показанное на рис. 3 внизу справа.

В этом диалоговом окне вводится следующая информация.

Find:

Parameter — выбор оптимизируемых параметров;

Low — минимальное значение оптимизируемого параметра (вводится);

High — максимальное значение оптимизируемого параметра (вводится);

Step — шаг изменения оптимизируемого параметра (вводится при выборе метода Stepping Powell);

Current — текущее значение оптимизируемого параметра (индицируется);

Optimized — поиск наиболее подходящего значения оптимизируемого параметра (индицируется);

That — выбор критерия(ев) оптимизации.

Method — выбор метода оптимизации:

Standard Powell — стандартный метод оптимизации Пауэлла,

Stepping Powell — согласно этому методу параметры изменяются от значения Low до значения High с шагом Step. На каждом шаге изменения параметров применяется стандартный метод Пауэлла.

Total Error — корень квадратный из суммарной ошибки (разности между целевой функцией и ее фактической величиной); выводится когда выбрано поле Equates в группе THAT.

Constraints — ограничения типа неравенств и равенств, записываемые на четырех строках, например, PD(R1)<=100m, V(Out)>=1.2, VCE(Q1)*IC(Q1)<=200m

Optimize — начало оптимизации.

Stop — остановка оптимизации.

Apply — изменение на схеме значения параметров в соответствии с результатами оптимизации.

Format — выбор формы представления чисел.

Close — завершение режима оптимизации.

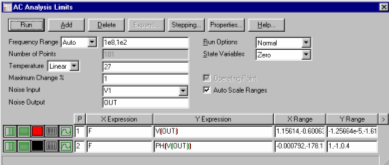
В приведенном примере требуется изменением L1, C1, R1 добиться такого вида АЧХ, чтобы она максимально близко проходила возле 6 заданных точек (частота, амплитуда в дБ): (2e6, 2.188), (4e6, 10.449), (6e6,-1.696), (8e6,-9.103), (10e6, -13.939), (20e6,-27.134). Это означает, что корень квадратный из суммы квадратов отклонений полученной АЧХ от заданных значений в заданных точках принимает минимальное значение. В соответствии с заданной целевой функцией и заполняются поля группы THAT в окне OPTIMIZE (см. рис. 4.18, 4.19). Например Y_Level(DB(V(OUT)),1,1,2e+006) обозначает значение кривой оптимизируемой характеристики (АЧХ в дБ) при значении независимой переменной (частоты) равной 2E6 Hz. Выбор Equates означает, что оптимизация идет для наилучшего удовлетворения условию равества коэффициента передачи в дБ заданному значению 2.188.

Отметим, что в группе THAT вместо Equates может быть выбрано Minimize или Maximize, тогда оптимизация выполняется с целью достижения минимального (максимального) значения кривой Y в выбранной точке X. См. примеры OPT1…OPT3 из каталога Analysis\Optimize.

Заполнение полей группы FIND в рассматриваемом примере осуществляется в соответствии с оптимизируемыми параметрами R1, C1, L1 (поля Parameter) и заданными диапазонами их изменения (поля Low и High).

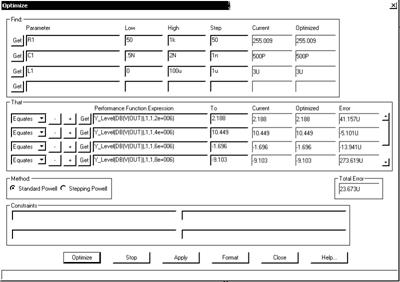
Рис. 4. Вид окна Optimize после проведения оптимизации

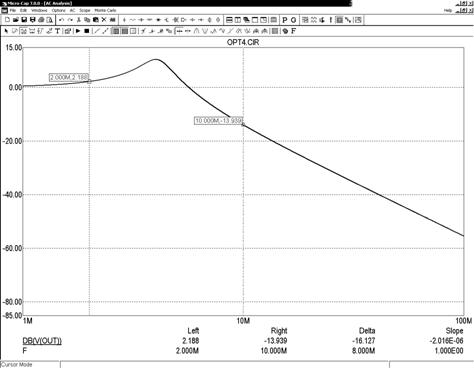
Рис. 5. Вид АЧХ схемы после оптимизации

После заполнения диалогового окна нажатием на панель Optimize выполняют оптимизацию (см. рис. 4) и затем при необходимости нажатием на панель Apply переносят найденные оптимальные значения параметров на схему. Выполняемый после таких действий анализ выведет характеристики схемы при полученных оптимальных значениях параметров (см. рис. 5). По его результатам пользователь может проверить соответствие выполненной оптимизации техническому заданию.

4 Статистический анализ по методу Монте-Карло

При выборе режимов моделирования Transient, AC или DC становится доступен подрежим Monte Carlo для расчета характеристик цепей при случайном разбросе параметров:

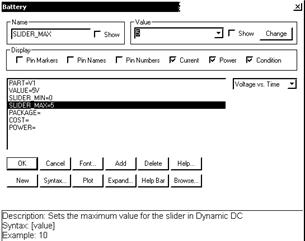
Options — установка параметров метода Монте-Карло (см. рис. 6);

Add Histogram — добавление окна гистограмм (доступно после проведения моделирования);

Delete Histogram — удаление окна гистограмм (доступно после проведения моделирования);

Statistics — статистическая обработка результатов (доступно после построения гистограммы).

В диалоговом окне Monte Carlo Options (рис. 6, а), открываемом по команде Monte Carlo/Options, указывается количество статистических испытаний Number of Runs (не более 30000) и характер закона распределения случайных параметров, заданных значением LOT параметра модели: Uniform равномерное распределение, Gauss — гауссово, Worst Case — наихудший случай. Напомним, что в окне Global Settings задается отношение разброса случайных параметров к среднеквадратическому отклонению SD.

Гауссово распределение (Gauss) случайной величины x описывается уравнением:

,

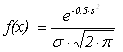Где , m — номинальное значение параметра, s — величина отклонения, указываемая после ключевого слова LOT (здесь абсолютное значение), x — значение случайной величины, f(x) — плотность вероятности принятия случайной величиной значения x.

Равномерное распределение (Uniform) — означает одинаковую вероятность принятия случайной величиной x любого значения внутри диапазона, определяемого параметром модели LOT.

а)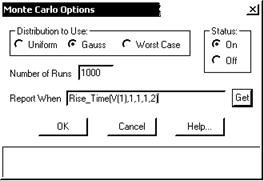

б)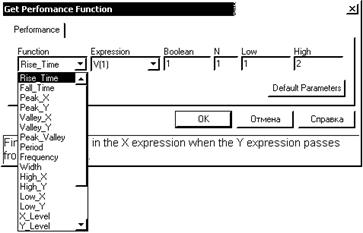

Рис. 6. Диалоговое окно Monte Carlo Options (а) и окно задания функций (б)

Наихудший случай (Worst case) соответствует равной вероятности (0.5) принятия случайной величиной минимально возможного и максимально возможного значения (см. пример CARLO2_LOT & DEV из каталога ANALYSIS\Monte Carlo).

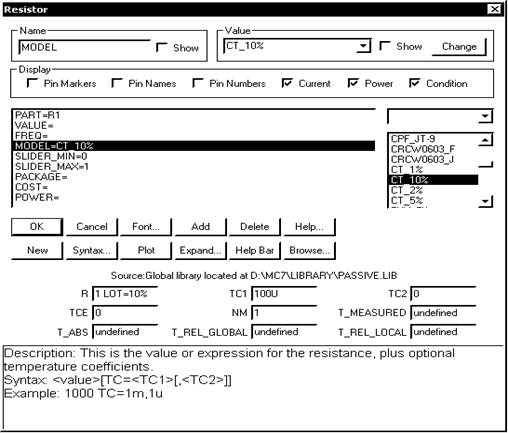
На строке Report When указывается условие, при выполнении которого выводится предупреждающее сообщение в тестовый файл результатов моделирования, имеющий расширение имени *.OUT. Имя указываемой на этой строке функции может быть выбрано в списке доступных функций (рис. 6, б), открываемом нажатием на клавишу Function. Перед выполнением расчетов по методу Монте-Карло следует поставить переключатель Status в положение On. Выделение параметров, имеющих случайный разброс, выполняется с помощью ключевых слов LOT и/или DEV.

Для расчета разброса значений параметров, имеющих разброс LOT и DEV, используются различные генераторы случайных чисел. В свою очередь параметры, имеющие признак DEV, получают независимые случайные значения, а имеющие признак LOT — коррелированные случайные значения в пределах параметров одного элемента. Ключевые слова LOT и DEV помещаются после номинального значения параметра и имеют формат:

[LOT=<paзброс>[%]][DEV=<paзбpoc>[%]]

Указывается либо абсолютное, либо относительное значение разброса в процентах (в последнем случае надо ввести знак %).

Примеры:

.model VIN SIN (F=10kHz A=10mV LOT=10% DC=0 PH=0 RS=1)

.model KT316B NPN (IS=2.8f LOT=5% BF=75 LOT=5% DEV=20%)

.MODEL IND1 IND (L=1.0 LOT=10% )

.MODEL CAP2 CAP (C=1.0 LOT=10% )

.MODEL RMOD RES (R=1 LOT=10%)

Во втором примере параметр BF имеет некоррелированный разброс DEV=20% и, кроме того, разброс LOT = 5%, коррелированный с изменением параметра IS.

  

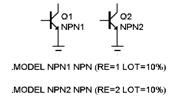
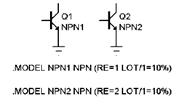
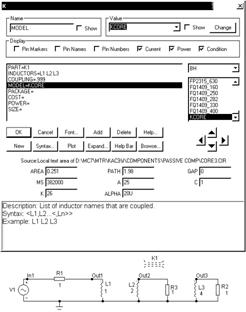
Рис. 7. Использование LOT и DEV

В примере рис. 7, а RE транзистора Q1 имеет случайный разброс независимый от случайного разброса RE транзистора Q2 (они создаются разными генераторами случайных чисел). В примере рис. 7, б сопротивления RE обоих транзисторов Q1 и Q2 имеют коррелированный разброс, однако их значения не будут одинаковыми из-за различия номиналов. В примере 4.22, в случайные разбросы RE (в пределах заданного диапазона LOT) обоих транзисторов коррелированы, однако в целом разбросы не связаны из-за использования различных генераторов для DEV. DEV задает относительное изменение параметра в процентах в сторону увеличения или уменьшения после вычисления случайной величины по значению LOT в соответствии с заданным законом распределения (См. пример CARLO2_LOT & DEV).

 

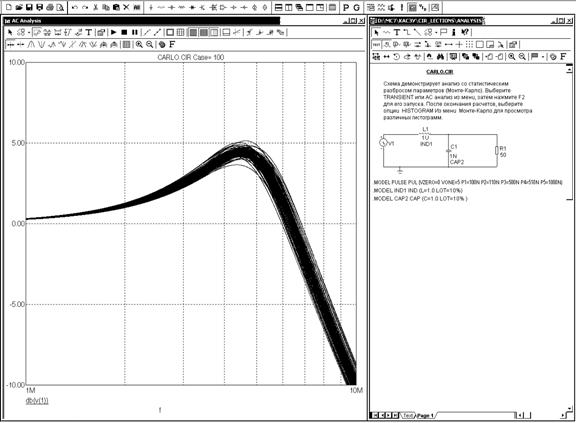
Рис. 8. Семейство реализаций переходного процесса при случайных назависимых разбросах индуктивности и емкости

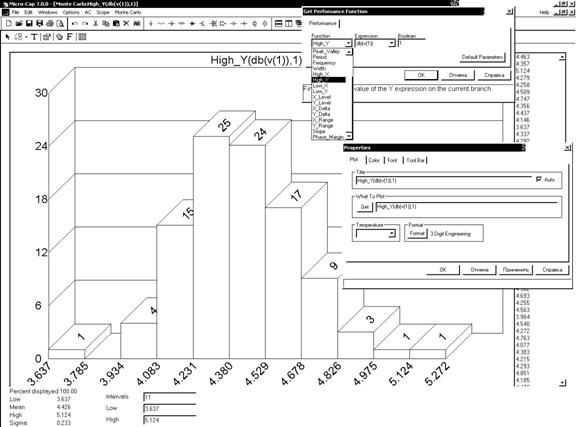
Рис. 9. Окно построения гистограмм

Допустим, что в режимах Transient, AC или DC анализируется некоторая функция цепи y=f(x), где х — независимая переменная (время, частота, входное постоянное напряжение или ток), у — зависимая переменная (узловой потенциал, входное сопротивление и т. п.). Для каждой реализации процесса у(х) рассчитывается глобальная характеристика F (the collaction function), например максимальное значение реализации F=max{y(x)} (вводится HIGH_Y). Название характеристики F вводится, на строке Report When (см. рис. 6, а) или выбирается из окна Functions (рис. 6, б), открываемого нажатием на клавишу GET (см. рис. 6, а).

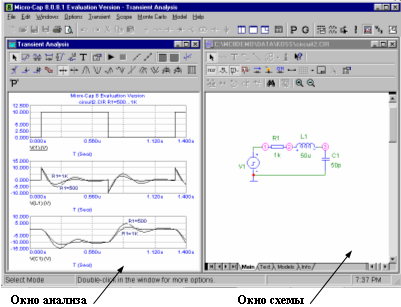
После установки параметров начинают моделирование выбором пункта Run в меню моделирования выбранного типа или нажатием F2. Реализации характеристик цепи у(х) выводятся на экран дисплея в виде семейства графиков, как в качестве примера показано на рис. 8 при расчете частотных характеристик резонансного контура.

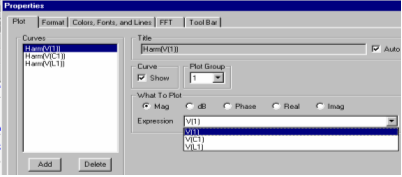
Статистическая обработка результатов моделирования производится по команде Monte Carlo/Histograms/Add Histograms. Ее результаты представляются в виде гистограммы, примерный вид которой показан на рис. 9. Двойной щелчок курсором мыши, расположенном в окне гистограмм, открывается диалоговое окно задания параметров Properties (закладка Plot), оно же открывается в начале выполнения команды Add Histograms. В нем в строке Function (вызываемой нажатием клавиши GET) указывается имя анализируемой функции F, а в строке Expression — имя характеристики цепи у (см. рис. 9).

На графике гистограммы по горизонтальной оси откладываются значения характеристики F, по вертикали — вероятности в процентах.

Значения характеристики F во всех реализациях выведены в окне в правой части экрана. Ниже гистограмм располагается окно, в котором можно задать количество интервалов разбиения области определения анализируемой характеристики F (Intervals) и значения ее границ (Low, High).

В нижней части экрана слева помещается следующая статистическая информация: Low — минимальное значение характеристики, Mean — ее среднее значение, High — максимальное значение, Sigma — среднеквадратическое отклонение случайной величины F.

Результаты статистической обработки заносятся также в текстовый файл после выбора подкоманды Monte Carlo/Statistics. Текстовая информация размещается в файлах, имеющих то же имя, что и имя схемы, и расширения имени .АМС, .DMC, .ТМС в зависимости от вида анализа. Примеры статистического анализа см. в схемных файлах CARLO, CARL02, CARLO4 подкаталога Analysis\Monte Carlo.

5 Анимация и трехмерные графики

Режим анимации есть один из способов просмотра результатов моделирования. После нажатия в режиме Analysis на кнопку  (Animate) выводится диалоговое окно, в котором выбирается способ построения графиков:

Don't wait — выключение режима анимации (построение графиков без дополнительной задержки), обеспечивается максимальная скорость построения графиков;

Wait for Key Press -- задержка построения очередной точки графиков до нажатия указанной комбинации клавиш CTRL+<пробел>;

Wait for time Delay — включение режима анимации, при котором очередная точка графиков строится с указанным запаздыванием (по умолчанию установлено запаздывание 0,5 с).

Для построения примера трехмерного графика загрузим пример 3D1.cir из каталога PROBE_3D и в режиме Transient выполним моделирование переходных процессов. После этого выполним команду Transient/3D Window/Add 3D Plot и в открывшемся диалоговом окне выберем переменные, откладываемые по осям X, Y и Z (можно просто выбрать DROP vs T vs R1). Затем нажатием клавиши ОК построим трехмерный график — в рассматриваемом примере это зависимость выходной функции Drop от времени Т и сопротивлении R резистора R1. Выходная переменная указывается в виде выражения, указываемого на двумерном графике в графе Y Expression. См. также пример 3D2.cir из каталога PROBE_3D.

Заключение

Все перечисленные выше режимы анализа являются разновидностями анализа по постоянному току и выполняются при исключении из схемы конденсаторов и закорачивании катушек индуктивности.

Перечисленные достоинства делают пакет программ MicroCAP-7 весьма привлекательным для моделирования электронных устройств средней степени сложности. Удобство в работе, нетребовательность к ресурсам компьютера и способность анализировать электронные устройства с достаточно большим количеством компонентов позволяют успешно использовать этот пакет в учебном процессе. В данной работе рассмотрены лишь основные сведения, необходимые для начала работы с пакетом и анализа большинства электронных схем, изучаемых в специальных дисциплинах и используемых при курсовом и дипломном проектировании. В случае необходимости дополнительные (и более подробные) сведения могут быть получены из встроенной подсказки системы (вызывается клавишей <F1> или через меню HELP/Contens).

Список литературы

1.  Разевиг В.Д. Схемотехническое моделирование с помощью Micro-CAP 7. — Горячая линия-Телеком, 368 с. 621.38 Р-17 /2003 – 9 аб, 2 чз

2.  Разевиг В.Д. Система моделирования Micro-Cap 6. – М.: Горячая линия-Телеком, 2001. — 344 с., ил.

3.  Разевиг В.Д. Система сквозного проектирования электронных устройств Design Lab 8.0. – Москва, «Солон», 1999. 004 Р-17 /2003 – 1 аб/ 2000 – 11 аб, 5 чз

4.  Micro-Cap 7.0 Electronic Circuit Analysis Program Reference Manual Copyright 1982-2001 by Spectrum Software 1021 South Wolfe Road Sunnyvale, CA 94086