Навигация
Основні поняття та загальна схема структури математичних здібностей
2.1 Основні поняття та загальна схема структури математичних здібностей
Перш ніж визначити основні поняття, з якими ми будемо мати справу надалі, необхідно відзначити, що математичні здібності можуть мати свій вираз на, різних рівнях діяльності. Поняття математичні здібності ми трактуватимемо в двох аспектах:
а) як творчі (наукові) здібності − здатності до наукової математичної діяльності, що дає нові і об'єктивно значущі для людства результати, досягнення, цінний в суспільному відношенні продукт;
б) як учбові здібності − здібності до вивчення (навчанню, засвоєнню) математики (в даному випадку шкільного курсу математики), швидкого і успішного оволодіння відповідними знаннями, уміннями, навиками.
Зрозуміло, якщо розглядати питання в загальному плані, то можна сказати, що здібності в порівнянні з уміннями і навиками в більшості випадків формуються і змінюються повільніше, насилу, є стійкішими утвореннями. Але ставити цей принцип в основу розрізнення вказаних категорій все-таки неможливо, оскільки розрізнення по параметрах «більше - менше», «швидше - повільніше» абсолютно беззмістовно і якісно невизначено.
У дослідженні математичних здібностей виходити з іншого розуміння істоти здібностей і умінь, навиків. Початковим при цьому був факт, що при аналізі здібностей завжди мають на увазі якості, особливості людини, що виконує ту або іншу діяльність, а при аналізі умінь і навиків − якості, особливості діяльності, яку здійснює людина. У основі визначення поняття «здатність» в будь-якому радянському підручнику психології, майже в будь-якій праці, що стосується психології здібностей, завжди лежить характеристика індивідуально-психологічних особливостей людини. З іншого боку, всі визначення навиків, умінь виходять з поняття дії
Здібності - це не навики і уміння, а ті індивідуально-психологічні особливості, від яких заві легке і успішне оволодіння уміннями і навиками у відповідній діяльності.
Загальна схема структури математичних здібностей в шкільному віці представляється таким чином (розглядати її будемо, як і раніше, виходячи з основних етапів вирішення завдань):
1. Отримання математичної інформації
а) Здібність до формалізованого сприйняття математичного матеріалу, схоплювання формальної структури завдання.
2. Переробка математичної інформації
а) Здібність до логічного мислення у сфері кількісних і просторових стосунків, числовою і знаковою символіки. Здатність мислити математичними символами.
б) Здібність до швидкого і широкого узагальнення математичних об'єктів, стосунків і дій.
в) Здібність до згортання процесу математичного, міркування і системи відповідних дій. Здатність мислити згорнутими структурами
г) Гнучкість розумових процесів в математичній діяльності
д) Прагнення до ясності, простоти, економності ірраціональності рішень.
е) Здібність до швидкої скованої перебудови спрямованості розумового процесу перемиканню з прямого на зворотний хід думки (оборотність розумового процесу при математичному міркуванні).
3. Зберігання математичної інформації
а) Математична пам'ять (узагальнена пам'ять на, математичні стосунки, типові характеристики, схеми і доказів, методи вирішення завдань і принципи підходу до них.)
4. Загальний синтетичний компонент
а) Математична спрямованість розуму.
Виділені компоненти тісно зв'язані, впливають один на одного і утворюють в своїй сукупності єдину систему, цілісну структуру, своєрідний синдром математичної обдарованості, математичний склад розуму.
Не входять в структуру математичної обдарованості .те компоненти, наявність яких в цій структурі не обов'язково (хоча і корисно). У цьому сенсі вони є нейтральними по відношенню до математичної обдарованості. Проте їх наявність або відсутність в структурі (точніше, ступінь розвитку) визначають тип математичного складу розуму. Не є обов'язковими в структурі математичної обдарованості наступні компоненти:
Швидкість розумових процесів як тимчасова характеристика. Індивідуальний темп роботи не грає вирішального значення. Математик може роздумувати неквапливо, навіть поволі, але дуже докладно і глибоко.
Обчислювальні здібності (здібності до швидких і точних обчислень, часто в думці). Відомо, що є люди, здатні проводити в думці складні математичні обчислення (майже миттєве зведення в квадрат і куб тризначних чисел, витягання кубічного кореня з шестизначних чисел), але не уміючі вирішити скільки-небудь складного завдання. Відомо також, що існували і існують феноменальні «лічильники», не що дали математиці нічого, а видатний французький математик А. Пуанкаре писав про себе, що без помилки не може зробити навіть додавання.
Пам'ять на цифри, числа, формули. Як указував академік А. Н. Колмогоров, багато видатних математиків не володіли видатною пам'яттю такого роду.
Здібність до просторових уявлень.
Здатність наочно представити абстрактні математичні стосунки і залежності.
Слід підкреслити, що схема структури математичних здібностей має на увазі математичні здібності школяра. Не можна заздалегідь, до спеціального вивчення, сказати, якою мірою її можна вважати за загальну схему структури математичних здібностей, якою мірою її можна віднести до обдарованих математиків, що цілком склалися.
Зрозуміло, конкретний зміст структури здібностей неабиякою мірою залежить від методів навчання, оскільки вона складається в процесі навчання. Але встановлені нами компоненти за всіх умов повинні входити в цю структуру. Неможливе прсдставіть наприклад, щоб при якій-небудь системі навчання здібність до узагальнення або математична пам'ять не входили в структуру математичних здібностей.
Аналізуючи схему структури математичної обдарованості, ми можемо відмітити, що певні моменти в характеристиці перцептивні, інтелектуальні і мнемічні сторони математичної діяльності мають загальне значення. Наприклад, формалізоване сприйняття завдання − це сприйняття узагальнене, згорнуте, гнучке; математична пам'ять − це пам'ять на узагальнені, згорнуті і гнучкі системи. Якщо ми говоримо про формалізоване (узагальненому) сприйняття умов завдання, то можна говорити і про формалізоване (узагальненому) рішення, про формалізоване (узагальненому) запам'ятовування. Тому розгорнену схему структури можна представити і в іншій, надзвичайно стислій формулі: математична обдарованість характеризується узагальненим, згорнутим і гнучким мисленням у сфері математичних стосунків, числової і знакової символіки і математичним складом розуму. Ця особливість математичного мислення приводить до збільшення швидкості переробки математичної інформації і, отже, економії нервово-психічних сил. В термінах асоціативної теорії це звучало б так: математичні здібності − це здібності до освіти на математичному матеріалі узагальнених, згорнутих, гнучких, і оборотних асоціацій і їх систем. Вказані здібності різною мірою виражені у здібних, середніх і нездібних учнів. У здатних за деяких умов такі асоціації утворюються «з місця», при мінімальній кількості вправ. У нездібних же вони утворюються з надзвичайною працею. Для середніх же що вчаться необхідною умовою поступового утворення таких асоціацій є система спеціально організованих вправ, тренування. Провівши первинний аналіз математичних, здібностей, отримавши уявлення про їх структуру, ми не вважаємо що на цьому дослідження компонентів математичних здібностей може бути закінчене. Необхідне поглиблення вивчення кожного компоненту з метою проникнути в його природу; виявити його фізіологічні основи.
Похожие работы
... чинників на розвиток творчих здібностей учнів. 1.2 Теоретичне обґрунтування проблеми розвитку творчих здібностей учнів 7-9 класів на уроках фізики на засадах моніторингового підходу Формування й розвиток творчих здібностей учнів виступають сьогодні однією з актуальних проблем української системи освіти. Розвиток та виховання здібних і талановитих дітей відповідає потребі формування творчого ...
... і правила, формули, тотожності, а також означення і теореми у програмі - послідовності кроків розв'язування задач відповідних видів. 2.3 Проблемні задачі як засіб розвитку творчих здібностей учнів На уроках математики практикують різні прийоми, щоб формувати в дітей критичне та логічне, творче мислення. Розв’язуючи задачу, дають такі завдання - змінити умову таким чином, щоб вона розв’ ...
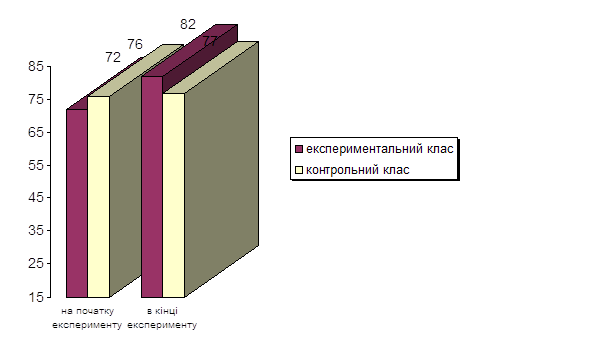
... ійований підхід, значно вищий, ніж у контрольному, причому особливо відрізняються результати розв’язання додаткового завдання. Ми пояснюємо це цілеспрямованою роботою диференційованого підходу у процесі навчання молодших школярів розв’язувати текстові задачі, яка проводилася відповідно до завдань формуючого експерименту, що привело до позитивних зрушень у розвитку мислення школярів. 2.3 Аналіз ...
... ійна підготовка майбутніх учителів початкових класів в умовах інформаційного суспільства. Предмет дослідження – формування інформаційної культури майбутнього вчителя початкових класів у процесі професійної підготовки. Мета дослідження полягає у визначенні теоретичних і методичних засад формування ІК як основної складової професійної культури майбутнього вчителя початкових класів і засобу полі ...




0 комментариев