Поняття про здібності
Задатки як природні передумови здібностей і таланту та їх відмінність
Розвиток здібностей
Основні поняття та загальна схема структури математичних здібностей
Вікові особливості формування та розвитку математичних здібностей
Про статеві відмінності в характеристиці математичних здібносте
Розвиток творчих здібностей учнів та дослідження
Навигация
Розвиток творчих здібностей учнів та дослідження
Формування та розвиток математичних здібностей
78051
знак
0
таблиц
0
изображений
2.4 Розвиток творчих здібностей учнів та дослідження
Коли йдеться про зміст шкільного курсу математики, то, звичайно, мають на увазі засвоєння учнями певної системи математичних знань, умінь і навичок. Але не можна зводити все математичне навчання в шкоді до передачі учням визначеної суми знань і навичок. Це обмежувало б роль математики в загальній освіті. Тому перед школою стоїть важливе завдання математичного розвитку учнів.
Математичні здібності — це здатність утворювати на математичному матеріалі узагальнені, згорнуті, гнучкі й обернені асоціації та їх системи. До складових математичних здібностей слід віднести:
а) здатність до формалізації математичного матеріалу, відокремлення форми від змісту, абстрагування від реальних ситуацій і їх кількісних відношень та просторових форм; оперування структурами відношень і зв'язків;
б) здатність до узагальнення матеріалу;
в) здатність до оперування числовою і знаковою символікою;
г) здатність до логічних міркувань, пов'язаних з потребою доводити, робити висновки; здатність до скорочення процесу міркувань;
д) здатність до переходу від прямого до оберненого ходу думки;
е) гнучкість мислення незалежно від впливу шаблонів.
Математика сприяє виробленню особливого виду пам'яті − пам'яті, спрямованої на узагальнення, творення логічних схем, формалізованих структур, виховує здатність до просторових уявлень. Наявність математичних здібностей в одних учнів і недостатня розвинутість їх в інших вимагає від учителя постійного пошуку, шляхів формування і розвитку таких здібностей у школярів. Рівневі диференціації з урахуванням психології математичних здібностей учнів збільшує можливості роботи вчителя. Такий підхід створює умови для розвитку здібностей учнів, які мають природжені задатки до занять математикою, і забезпечує посильною роботою учнів, які не мають таких задатків. Виконуючи посильні завдання, учень отримує впевненість у своїх силах.
Усі задачі поділяються на три типи:
а) задачі, які розв'язую для кращого засвоєння теорії;
б) тренувальні вправи, мета яких − виробити навички;
в) задачі, за допомогою яких розвиваються математичні здібності учнів.
Розв'язування задач − це робота дещо незвичайна, адже вона є розумовою. А щоб навчитися будь-якій роботі, треба спочатку добре вивчити той матеріал, над яким доведеться працювати, ті інструменти, з допомогою яких буде виконуватись робота.
Отож, для того щоб навчити учнів розв'язувати задачі, потрібно розібратись в тому, що вони собою являють, як побудовані, з яких частин складаються, що потрібно знати, щоб розв'язати ту чи іншу задачу. Учні п'ятого класу вже знають, що під математичною задачею розуміють будь-яку вимогу обчислити, побудувати, довести що-небудь, пов'язане з числовими величинами або геометричними фігурами. Арифметичною задачею називають вимогу знайти числове значення деякої величини, якщо дано числове значення інших величин і залежність, яка зв'язує їх як між собою, так і з шуканою величиною. У початкових класах в основному розглядаються так звані сюжетні задачі, в яких описується кількісна сторона деяких явищ.
Сюжетну задачу, для розв'язання якої треба виконати дві чи більше пов'язаних між собою арифметичних дій, називають складеною. Щоб розв'язати складену задачу, пропонують учням спочатку скласти план розв'язування. План складається на основі аналізу задачі, який проводять від числових даних або від запитання. Аналізу задачі передує ґрунтовне вивчення умови і запитання задачі.
Наприклад, задача. Велосипедист їхав 4 години із швидкістю 12 км/год. Йому залишилося проїхати на 16 км менше, ніж він проїхав. Яку відстань потрібно було проїхати велосипедисту?
Аналіз від числових даних. Відомо, що велосипедист їхав 4 години із швидкістю 12 км/год. За цими даними можна дізнатися, яку відстань проїхав велосипедист. Для цього треба швидкість помножити на час. Знаючи відстань, яку вже проїхав велосипедист, і те, що залишилося проїхати на 16 км менше, можна знайти відстань, яку залишилося проїхати. Для цього відстань, яку вже проїхав велосипедист, треба зменшити на 16 км. Знаючи, скільки кілометрів залишилося їхати, можна знайти весь шлях. Для цього треба виконати додавання знайдених відстаней.
Аналіз від запитання. У задачі треба знайти весь шлях, який має проїхати велосипедист. Ми не можемо одразу відповісти на це запитання, бо не відомо, скільки велосипедист вже проїхав і скільки йому залишилося їхати. Щоб знайти пройдений шлях, треба знати швидкість і час руху. Це в задачі відомо. Помножимо швидкість на час і дізнаємося про пройдений шлях. Відстань, яку велосипедист ще має проїхати, можна також знайти. Для цього знайдену відстань треба зменшити на 16 км. Отже, план розв'язування задачі такий:
Скільки кілометрів проїхав велосипедист за 4 години?
Скільки кілометрів велосипедисту залишилося проїхати?
Яку відстань мав проїхати велосипедист?
Отже, підвищення ефективності навчання математики можна досягти, продуктивно реалізуючи всі дидактичні функції математичних задач. Велику роль відіграють задачі, які учні складають самі. Складання задачі часто вимагає роздумів, які під час розв'язку готових задач не потрібні. Тому складання задач сприяє розвитку творчого мислення учнів. Щоб вивчення математики викликало в учня задоволення, треба, щоб він заглибився у суть ідеї цієї науки, відчув внутрішній зв'язок усіх ланок міркувань, які дають можливість зрозуміти і саме доведення, і його логіку. Якщо учень хоча б раз досяг ясності в розумінні суті, проник у внутрішній зв'язок понять і логічних висновків, то йому буде важко задовільнитися потім заучуванням без. розуміння. І тоді він здійснятиме відкриття: процес власної думки вимагає значно менших зусиль і витрат часу, ніж вивчення напам'ять. Щоб привчити учнів самостійно мислити, викликати в них віру у власні сили і розумна також виховати впевненість у своїх можливостях, необхідно примусити їх пройти через певні труднощі, а не подавати все в готовому вигляді.
У системі розвиваючого навчання під час вивчення математики важливе місце посідає обчислювальна практика. На 5-6 класи припадає основний обсяг роботи обчислень з раціональними числами. У наступних класах ці навички розвиваються і закріплюються, зростає питома вага наближених обчислень, використовується прикидка, оцінювання результатів обчислень. Широке використання мікрокалькуляторів не зменшує ролі обчислень без них і особливо усного виконання дій. Адже, користуючись мікрокалькуляторами, треба вміти робити прикидку очікуваного результату й округлювати його до потрібної точності, замінюючи деякі операції усним виконанням, уміти проаналізувати здобуту інформацію.
Слід мати на увазі і розвиваючу функцію усних обчислень: вони активізують увагу і пам'ять учнів, спонукають їх до раціональної діяльності. Якщо в учнів середніх класів добре сформовані ці навички, це є запорукою того, що в старших класах розв'язування задач не буде викликати особливих труднощів. Уміння розв'язувати ту чи іншу задачу залежить від багатьох чинників. Але передусім необхідно навчитися розрізняти основні типи задач і уміти розв'язувати найпростіші з них. Задачі, що розв'язуються у шкільному курсі математики, можна умовно розподілити на такі типи задач:
а) задачі «на рух»;
б)задачі «на сумісну роботу»;
в) задачі «на планування»;
г) задачі «на залежність між компонентами арифметичних дій»;
д) задачі «на відсотки»;
е) задачі «на суміші»;
є) задачі «на розбавлення»;
ж) задачі «з буквеними коефіцієнтами”;
з) інші види задач.
Природа математичних здібностей
Математичні здібності не вроджені, а набуті в житті властивості, причому формування цих властивостей виникає на основі певних задатків. Роль задатків різноманітна, в залежності від того, про які здібності йде мова, − ця роль мінімальна у випадках розвитку звичайних здібностей до математики, і винятково велика, коли мова йде про математичні здібності вчених-математиків.
Виділяють деякі факти, які особливий інтерес для . а саме:
1) часто дуже раннє формування здібностей до математики, нерідко в не найкращих умовах і при відсутності на перших етапах систематичного і ціленаправленого навчання; 2) цікавість та схильність до вивчення математики, які також часто проявляються в ранньому віці; 3) велика працездатність в області математики, яка зв’язана з відносно малою втомою в процесі напружених занять з математики; і 4) математична направленість розуму, що характеризує дуже здібних до математики людей.
Все це дозволяє підкреслити гіпотезу про роль вроджених функціональних особливостей мозку у випадку особливо математично-здібної людини.
Досвід роботи вчителів показує, що для поліпшення розуміння, закріплення та відтворення інформації доцільно проводити такі уроки як: урок-змагання; урок-вікторина, урок - “круглий стіл”; урок-гра та ін. Щоб зацікавленість учнів до вивчення математики не знижувалась, доречно систематично проводити ігри з використанням інтерактивних технологій.
Позакласна робота з математики дуже важлива для пробудження в учнів інтересу до математики. Тому математичні вікторини, змагання, ігри, прес-конференції, вечори сприяють підвищенню математичної культури, розширюють і поглиблюють здобуті на уроках знання, показують застосування їх на практиці, розвивають мислення, математичні здібності, допомагають ввійти у світ наукових і технічних ідей.
Так при проведенні прес-конференції “Гранітна опора наук” учні 7-9 класів багато дізналися про значення математики в різних галузях людської діяльності. Така форма роботи сприяє розширенню кругозору учнів, розвиткові уміння самостійно й творчо працювати з навчальною, науково-популярною літературою, формуванню в дітей інтересу до математики, а також поглибленню знань.
Учням дуже подобається брати участь в іграх, правила яких максимально наближені до умов тих ігор, за якими вони мають можливість спостерігати з екранів телевізорів. Такими іграми є “Перший мільйон”, “Поле чудес”, “Слабка логіка” та інші.
Щоб розвинути творчі здібності учнів, поступово та систематично залучати до самостійної пізнавальної діяльності, щоб забезпечити співпрацю між учнями та учителем, традиційного уроку недостатньо. Саме тому для проведення досліду я вибрала урок-бізнес.
Учнів класу було поділено на три команди, і весь урок вони працювали за груповим методом. Кожна команда сиділа за окремим великим столом. Ідея уроку полягала в тому, що учні - гості, які приїхали у місто «Відсоток», а вчитель - бізнесмен, мешканець цього міста, знайомить їх з ними і його мешканцями. Під час цієї мандрівки з учнями трапляються цікаві пригоди вони витрачають і заробляють гроші, займаються бізнесом, а допомагають їм у цьому відсотки. Урок проводився в класі де учням були знайомі усі типи задач на відсотки. Цей урок вимагає гарної підготовки вчителя. Було намальовано яскраві плакати з написами об'єктів продажу, картки з задачами, підготовано гральний кубик. У проведенні уроку вчителеві допомагали учні цього класу − «працівники фірми». Учень начальник фінансів − вів банківські рахунки команд на одній з відкидних дощок, троє менеджерів по одному біля кожного з трьох столів − для виплати коштів, зароблених учнем окремо та для того, щоб кидати гральний кубик.
Під час проведення цього уроку спостерігається велика зацікавленість учнів, вони активні, збуджені, працюють із задоволенням це можна пояснити, мабуть, тим, що учні відчувають себе у ролі бізнесменів, мають змогу заробити і витратити власний капітал. Це урок - міні-модель сучасного життя, де без знань відсотків та їх застосування не обійтись. Тому ми бачимо і мотиваційний бік цього уроку. Під час підведення підсумків я відзначаю не тільки командну роботу певної групи учнів, але й індивідуальні відповіді.
Така організація учбової діяльності на уроці дає можливість реалізувати принципи диференціації навчання, оскільки гарантує участь кожного учня на тому чи іншому етапі уроку. Так, учні з низьким рівнем навчальних здібностей можуть забезпечити команді бали на І етапі уроку, а учні з високими здібностями − виступи із захистом творчих робіт. Другий етап уроку − “поле діяльності” для учнів з середніми навчальними здібностями.
Попрацювавши деякий час з групою учнів, я помітила, що одні учні більш здатні до математики, ніж інші. Тому я вирішила провести тест «Чи маєш ти математичні здібності?». Завдяки йому я підтвердила свої здогадки і продовжила роботу трішки інакше. Дану групку учнів я поділила на дві підгрупки. З учнями, які мали кращі здібності до математики я продовжувала роботу як і раніше, а в підгрупці, де слабші учні я почала більш розвивати в них математичні здібності використовуючи різноманітні задачі. Потім знову провела даний тест і помітила, що рейтинг піднявся. Це означає що мені вдалося розвинути в учнів математичні здібності.
Я ще раз переконалася, що з готовими здібностями діти не народжуються. Тому їх постійно потрібно розвивати. А засвоєння дітьми знань з математики, є необхідною основою для вдосконалення та розвитку їх початкових математичних здібностей.
Висновок
При розгляді даної теми, ми ще раз переконалися, що Здібності − властивості душі людини, що розуміються як сукупність усіляких психічних процесів і станів. При чому Математичні здібності — це здатність утворювати на математичному матеріалі узагальнені, згорнуті, гнучкі й обернені асоціації та їх системи.
Ми вже знаємо, що з готовими здібностями діти не народжуються. Вони народжуються лише з внутрішніми передумовами до розвитку здібностей — з задатками. Здібності завжди є продуктом розвитку дитини, продуктом її навчання і виховання. Будучи складними психічними властивостями, здібності починають розвиватись не зразу. Щоб у дитини в тій чи іншій галузі діяльності виявились здібності, для цього потрібні певний рівень фізичного та психічного розвитку, певні знання і життєвий досвід. В окремих випадках здібності виявляються досить рано. Математичні здібності також проявляються дуже рано, та нажаль не у кожної людини вони є. Їх також потрібно постійно розвивати.
Щоб розвинути творчі здібності учнів, поступово та систематично залучати до самостійної пізнавальної діяльності, щоб забезпечити співпрацю між учнями та учителем, традиційного уроку недостатньо.
Здібності дітей виявляються в допитливості, в їх інтересах і нахилах до тих чи інших форм діяльності. Перехід дітей від початкового виявлення здібностей до вищих ступенів їх розвитку має своєю передумовою загальний розвиток дітей, дальше зміцнення їх фізичних та розумових сил і засвоєння ними. Засвоєння дітьми знань з математики, є необхідною основою для вдосконалення та розвитку їх початкових математичних здібностей. Розвиток здібностей дітей вимагає від них також спеціальних знань, умінь та навичок, які набуваються тривалими вправами в тих чи інших спеціальних галузях діяльності.
Без правильно побудованого навчання, без наполегливої праці над собою навіть «вундеркінди», тобто діти з рано виявленими визначними здібностями, стають пустоцвітами. Розвитком здібностей треба систематично керувати.
Література
1. Божик Л.М. Як розвивати розумові здібності. Година темат. спілкування.// Позакласний час – 2000 - №25 (додаток) – с 11 – 14.
2. Вовченко О.І. Про здібності людини. Талант. Урок №1 з питань психології // Позакласний час – 2003 – березень №6 (додаток №1) – с 45 – 47.
3. Губенко О.В. Розвиваємо математичні здібності дитини готуючи її до школи (Поради психолога).//Обдарована дитина – 1999 - №4 с 42 – 47.
4. Завуч – 2001 –лютий (додаток) - №6 с 2 – 16.
5. Ігри, ребуси, тести / Упоряд. О.В. Лєбора. – Х.: Веста: Видавництво «Ранок», 2007. – с.209 – 210. – (сучасна школа).
6. Крутецький В.А. Психология математических способностей школьников. М., «Просвещение», 1968г
7. М’ясоїд П.А. Здібності // М’ясоїд П.А. Загальна психологія: навч.посібник. – К. – 1998. – с 416 – 436.
8. Обдарована дитина-2007-№7 с 46 – 49, с 20 – 29.
9. Обдарована дитина-2005-№1 с 27 – 31.
10. Обдарована дитина-2003-№3 с 2 – 9.
11. Олексієнко Л. Як розвивати розумові здібності. Бесіда психолога з дітьми.//Шкільний світ. – 2001 – червень (№23) с 6 – 7.
12. Психологічний журнал.-1996-№2 с 80 – 88.
13. Терлецька Л.Г. Загальна характеристика здібностей людини//Психологічна газета – 2004 – листопад №22 с 3 – 4.
14. Федик О. Здібності як об'єкт психологічного аналізу// Психологія і суспільство. – 2002 – №1 – с 28 – 34.
Додатки
Чи маєш ти математичні здібності?
Дай свій варіант відповіді
1. У дюжині 4 гарних яблука. А скільки поганих?
2. У ящику 48 яблук, у кожній дюжині тільки 8 поганих. Скільки гарних яблук у ящику?
3. Яке число більше від 50 настільки, наскільки воно менше від 60?
4. Ти з приятелем витратива половину грошей у буфеті, а половину з того, що залишилося, на проїзд. Після цього у вас залишилося 40 копійок. Скільки ви витратили в буфеті?
5. За скільки годин машина може проїхати відстань, що дорівнює 400 км, зі швидкістю 50 км за годину?
6. Яке число більше від 36 настільки, наскільки воно більше від 29?
7. Твій годинник поспішає на 4 хв за добу. Якщо він показує о пів на восьму, то скільки він буде показувати опівдні?
8. Сума В і С дорівнює 116. В менше за А на 3, але більше від С на 4. Чому дорівнює А?
9. З кожних 100 осіб семеро не люблять їсти банани. Скільки осіб не люблять їсти банани з 500?
10. Банкір придбав 3 акції по 10 грн, а продав по 6 грн. По 6 грн він продав так само кожну з акцій, яку купив по 5. Якщо його прибуток становить 8 грн, скільки акцій він продав по 5 грн?
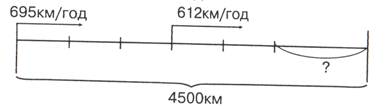
11. За який час літак пролетить відстань, що дорівнює 400 км, маючи швидкість 600 км за годину?
12. Якщо 6,5 м тканини коштують 26 грн, то скільки коштують 3,5 м тканини?
13. Якщо продуктів у супермаркеті вистачить для 300 покупців на 2 тижні, то на який час вистачить продуктів для 400 покупців?
14. Припустимо, що А, В, і С – числа. Д – сума цих чисел. Якщо від Д відняти А, чи буде це дорівнювати сумі В і С?
15. Припустимо, що А і В – числа. Д – різниця А і В. Якщо Д плюс А дорівнює В, то В більше за А?
16. 10 корів з’їдає за 10 днів 10 кг сіна. За скільки днів 1 корова з’їсть 1 кг сіна?
17. Продовж ряд чисел: 1, 1, 2, 6,
18. Впиши пропущені числа.
_ _ _ _
× 4
3 _ 3 2 _
19. Припустимо, що букви даного прикладу є числами. Якому числу відповідає кожна буква?
А 1 А
× 2 В
6 3 Д
О 2 О ч
О 8 Ю Д є
20. Припустимо, що букви даного прикладу є числами. Напиши відсутні букви.
5 Ж 4
× Ж 5 ж
2 К И Г
И К К 6 д
И И Ж 4 8 Г є
21. Серед 154 рукавичок зелених на 3 менше, аніж жовтих, але при цьому зелених на 5 більше, аніж синіх. Якщо всі рукавички зелені, жовті й сині, то скільки жовтих?
Ключ: Свої відповіді порівняйте з запропованими відповідями. За кожну співпавшу відповідь отримали 1 бал.
Відповіді:
1) 8; 2) 16;3) 55; 4) 80 копійок; 5) 8 год; 6 43; 7) на 1 хв 15 секунд; 8) 63; 9) 465; 10) 20 акцій; 11) за 40 хв; 12) 14 грн; 13) на 10 днів; 14) так; 15) так; 16) 10; 17) 24; 18) 7582·4=30 328; 19) А=2; Д=6; О=4; В=7; Ю=3; 20) Ж=4; Г=0; И=2; К=7; 21) 55.
Похожие работы
... чинників на розвиток творчих здібностей учнів. 1.2 Теоретичне обґрунтування проблеми розвитку творчих здібностей учнів 7-9 класів на уроках фізики на засадах моніторингового підходу Формування й розвиток творчих здібностей учнів виступають сьогодні однією з актуальних проблем української системи освіти. Розвиток та виховання здібних і талановитих дітей відповідає потребі формування творчого ...
... і правила, формули, тотожності, а також означення і теореми у програмі - послідовності кроків розв'язування задач відповідних видів. 2.3 Проблемні задачі як засіб розвитку творчих здібностей учнів На уроках математики практикують різні прийоми, щоб формувати в дітей критичне та логічне, творче мислення. Розв’язуючи задачу, дають такі завдання - змінити умову таким чином, щоб вона розв’ ...
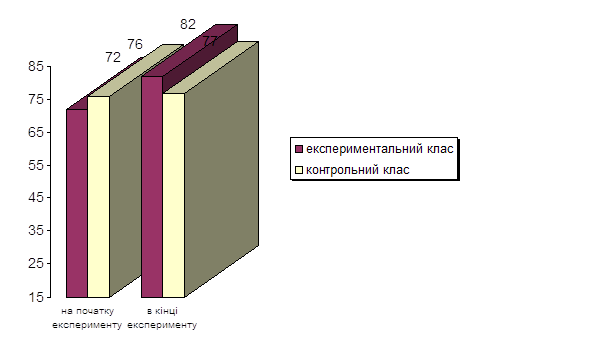
... ійований підхід, значно вищий, ніж у контрольному, причому особливо відрізняються результати розв’язання додаткового завдання. Ми пояснюємо це цілеспрямованою роботою диференційованого підходу у процесі навчання молодших школярів розв’язувати текстові задачі, яка проводилася відповідно до завдань формуючого експерименту, що привело до позитивних зрушень у розвитку мислення школярів. 2.3 Аналіз ...
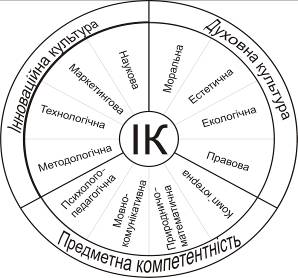
... ійна підготовка майбутніх учителів початкових класів в умовах інформаційного суспільства. Предмет дослідження – формування інформаційної культури майбутнього вчителя початкових класів у процесі професійної підготовки. Мета дослідження полягає у визначенні теоретичних і методичних засад формування ІК як основної складової професійної культури майбутнього вчителя початкових класів і засобу полі ...
0 комментариев