Цифровые вычислительные устройства и микропроцессоры приборных комплексов

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Уфимский государственный авиационный технический университет

Кафедра авиационного приборостроения

Лабораторный практикум

по теме

«Цифровые вычислительные устройства и микропроцессоры приборных комплексов»

 

Выполнил студент гр. АП-540

Табулдин Р.А.

Проверил преподаватель

Неретина В.В.

Кумертау 2010

ЛАБОРАТОРНАЯ РАБОТА № 1

ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ КОМБИНАЦИОННОГО ТИПА

 

1.1 Цель работы

Целью работы является ознакомление студентов с математическим аппаратом, описывающим действия цифровых устройств, развитие навыков составления логических уравнений, их минимизации, а также реализации на основе полученных уравнений комбинационных устройств с учетом имеющегося набора логических элементов.

Компьютерные модели логических схем устройства:

1)

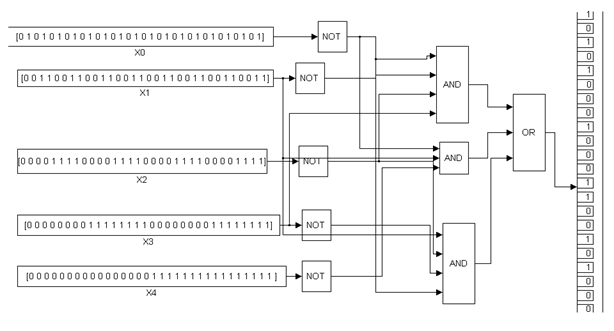
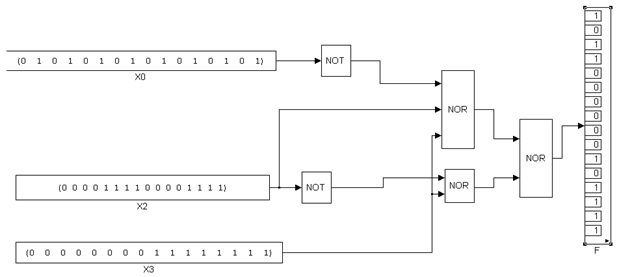
2)

3)

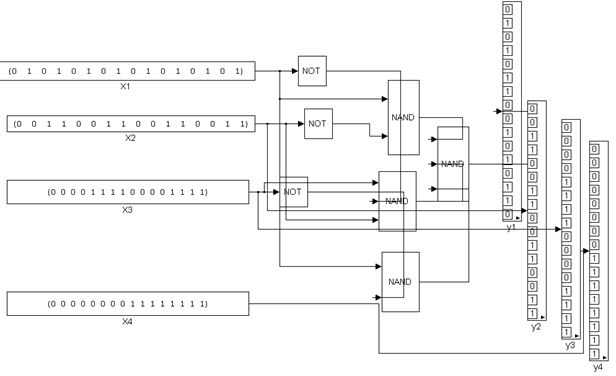
4)

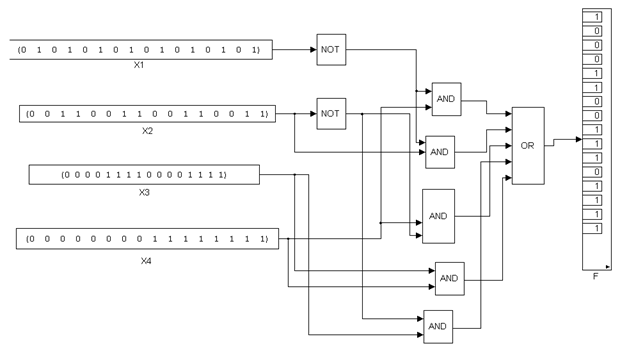
5)

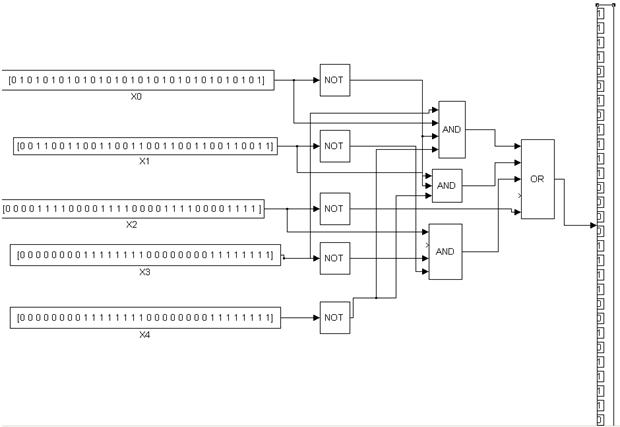
6)

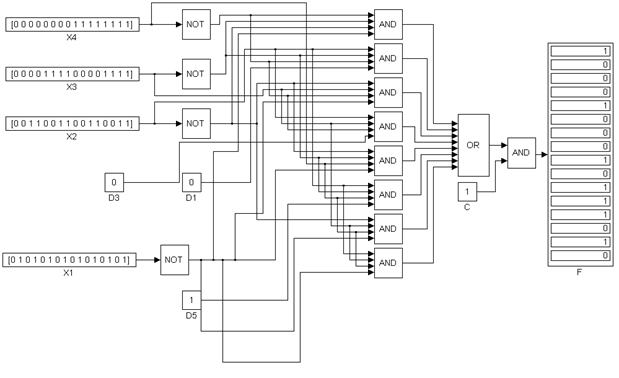
Вывод: ознакомился с математическим аппаратом, описывающим действия цифровых устройств, а также реализовал на основе полученных уравнений комбинационных устройств с учетом имеющегося набора логических элементов.

ЛАБОРАТОРНАЯ РАБОТА № 2

ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ ПОСЛЕДОВАТЕЛЬНОСТНОГО ТИПА

 

2.1 Цель работы

Целью работы является ознакомления студентов с принципами функционирования последовательностных устройств, а также изучение методов анализа и синтеза синхронных счетчиков с различными коэффициентами счета.

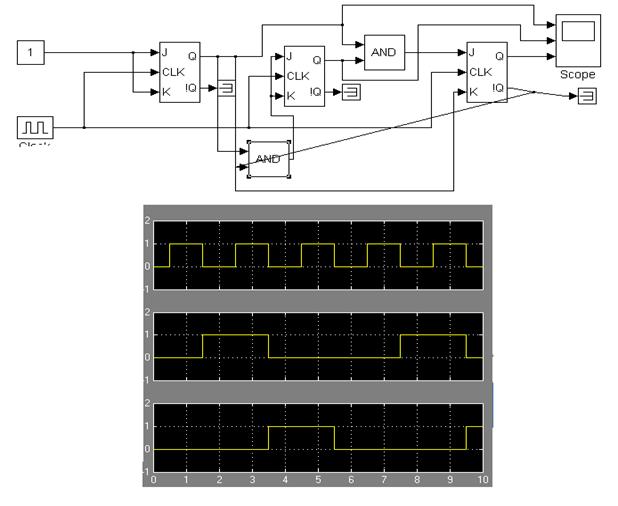
Компьютерные модели логических схем устройства:

1)

3)

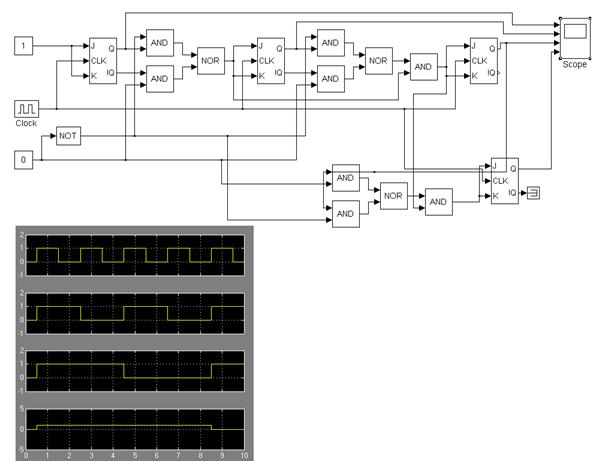
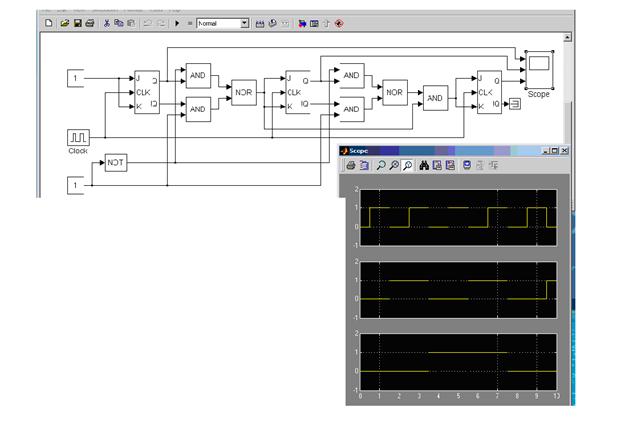
Вывод: ознакомился с принципами функционирования последовательностных устройств и изучил метод анализа и синтеза синхронных счетчиков.

ЛАБОРАТОРНАЯ РАБОТА № 3–6

ИЗУЧЕНИЕ СТРУКТУРНОЙ ОРГАНИЗАЦИИ И ПРИЕМОВ ПРОГРАММИРОВАНИЯ ОДНОКРИСТАЛЬНОГО

МИКРОКОНТРОЛЛЕРА К1816ВЕ48

 

3.1 Цель работы

Целью работы является изучение структурной организации, физического интерфейса, системы команд и средств расширения внутренних ресурсов однокристальных микроконтроллеров семейства МК48, а также освоение приемов программирования на языке ассемблера задач ввода и обработки данных, передачи управления, реализации средств реального времени.

Пример 1.1. Записать в РПД в ячейки с адресами 31Н и 32Н число 1C3FH:

LOAD: MOV R0,#31 ; загрузка в R0 указателя РПД

MOV @R0,#1C ; запись в РПД числа 1C

INC R0 ; продвижение указателя адреса РПД

MOV @R0,#3F ; запись в РПД числа 3F

Пример 1.2. Передать содержимое регистров банка 0 в ВПД, начиная с адреса 30H:

SEL RB1 ; выбор банка регистров 1

MOV R0,#30h ; определение начального адреса ВПД

MOV R1,#0 ; определение начального адреса банка

; регистров

MOV R2,#8 ; счетчик регистров (циклов) = 8

LOOP: MOV A,@R1 ; пересылка байта из регистра в ВПД

MOVX @R0,A ; через аккумулятор

INC R0 ; продвижение указателей

INC R1

DJNZ R2,LOOP ; продолжить, если переданы не все регистры

Пример 1.3. Вычислить произведение двух 4-битных чисел, расположенных в младших тетрадах регистров R0 и R1. Для вычисления используется таблица произведений для всех комбинаций сомножителей (всего 256). Произведение двух тетрад имеет формат 1 байт. Таким образом, необходимая таблица произведений занимает одну страницу памяти. Данную таблицу удобно разместить на третьей странице РПП:

; вычисление Z = X*Y

; R0 = 0000XXXX

; R1 = 0000YYYY

; X и Y принимают значения 0 и 1

ORG 0 ; директива ассемблера, задающая

; начальный адрес программы

MOV A,R0 ; пересылка множимого в аккумулятор

SWAP A ; обмен тетрад аккумулятора

ORL A,R1 ; формирование в аккумуляторе

; адреса произведения

MOVP3 A,@A ; загрузка в аккумулятор произведения

ORG 0300 ; директива ассемблера, задающая начальный

; адрес таблицы на третьей странице РПП директивы ассемблера, формирующие таблицу произведений

DB 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ; Z=0*Y

DB 1*0,1*1,1*2,…,1*0F ; Z=0*Y

…

…

…

DB 0F*0, 0F*1, 0F*2,…, 0F*0F ; Z=0*Y

Сложение положительных двоичных чисел. Выполнение этой операции покажем на примере:

Переносы 1 1 1

Первое слагаемое 0 0 1 1 0 1

Второе слагаемое 0 0 1 1 0 1

Сумма 0 1 1 0 1 0

Пример 1.4. Сложить содержимое регистра R7 и ячейки РПД с адресом 30Н:

MOV R0,#30h ; загрузка в R0 адреса РПД

MOV A,R7 ; загрузка операнда в аккумулятор

ADD A,@R0 ; сложение

Суммирование десятичных чисел. Способ суммирования десятичных чисел зависит от того, какой двоичный код выбран для представления десятичных цифр. Ниже рассматривается операция суммирования при использовании кода 8421.

Двоичные представления десятичных цифр суммируются по обычным правилам сложения двоичных чисел. Если полученная сумма содержит десять или более единиц, то формируется единица переноса, передаваемая в следующий десятичный разряд, а из суммы вычитаются десять единиц. Полученный результат есть цифра соответствующего разряда суммы. Наличие в полученной сумме десяти или более единиц выявляется по следующим признакам: появление переноса из разряда 8, возникающего при суммировании цифр; наличие единиц одновременно в разрядах 8 и 4 либо 8 и 2 в полученной сумме. При этом требуется коррекция суммы прибавлением к ней шести единиц (числа 0110₂).

Покажем эти действия на примерах.

– Сложить десятичные цифры 6 и 2 и перенос 1, поступающий из предыдущего десятичного разряда.

Десятичная система Код 8421

Переносы 1 1 1 1

Первая цифра 6 0 1 1 0

Вторая цифра 2 0 0 1 0

Сумма 9 1 0 0 1

Коррекция —

Результат 1 0 0 1

В этом случае полученное в результате суммирования число 1001₂ меньше десяти и коррекция суммы не требуется.

– Сложить десятичные цифры 8 и 9.

Десятичная система Код 8421

Переносы 1 0 1 0

Первая цифра 8 1 0 0 0

Вторая цифра 9 1 0 0 1

Сумма 7 0 0 0 1

Коррекция 0 1 1 0

Результат 0 1 1 1

– Сложить десятичные цифры 6 и 7.

Десятичная система Код 8421

Переносы 1 0 1 1 1 0

Первая цифра 6 0 1 1 0

Вторая цифра 7 0 1 1 1

Сумма 3 1 1 0 1

Коррекция 0 1 1 0

Результат 0 0 1 1

Пример 1.5. Сложить десятичные двоично-кодированные числа (BCD-числа), расположенные в A и R7:

ADD A,R7 ; двоичное сложение

DA A ; коррекция результата

Алгебраическое сложение с использованием дополнительного кода. Для сложения чисел со знаком необходимо отрицательное число перевести в дополнительный код. В двоичной системе счисления дополнительный код отрицательного числа формируется по следующему правилу: инвертируются (путем замены 0 на 1 и 1 на 0) цифры всех разрядов, кроме знакового, и в младший разряд прибавляется единица. Например, если =1 10110₂, то = 1 01010₂ (знаковые разряды выделены полужирным шрифтом). Обратное преобразование из дополнительного кода в прямой код производится по тому же правилу.

Рассмотрим примеры выполнения операции сложения.

Пусть =0 10110, =1 01101.

Переносы 1 1 1 1

Первое слагаемое 0 1 0 1 1 0

Второе слагаемое 1 1 0 0 1 1

Сумма 0 0 1 0 0 1

Как указывалось выше, перенос, возникающий из знакового разряда, отбрасывается.

Изменим на обратный знаки слагаемых (по отношению к предыдущему примеру): =1 10110, =0 01101. Очевидно, ожидаемый ответ = 1 01001.

Переносы 1

Первое слагаемое 1 0 1 0 1 0

Второе слагаемое 0 0 1 1 0 1

Сумма 1 1 0 1 1 1

Сумма 1 0 1 0 0 1

Таким образом, если результат сложения есть отрицательное число, то оно оказывается представленным в дополнительном коде.

Для вычитания 8-разрядных чисел без знака  может быть использовано выражение , где  – поразрядная инверсия . Другой способ вычитания может быть основан на следующем выражении: .

Пример 1.6. Вычитание байтов. Операция вычитания может быть выполнена двумя способами: переводом вычитаемого как отрицательного числа в дополнительный код с последующим сложением; переводом уменьшаемого в обратный код с последующей инверсией суммы.

Пусть требуется вычесть из A содержимое регистра R6. Вычитание выполнить в соответствии с выражением . Установка флага C после выполнения сложения будет свидетельствовать об отрицательном переполнении.

CPL A ; инверсия аккумулятора

ADD A,R6 ; сложение

CPL A ; инверсия суммы (получение разности)

Пример 1.7. Получить разность 2-байтных чисел без знака. Операнды располагаются в РПД. Адрес уменьшаемого хранится в R1, а вычитаемого – в R0. Результат поместить на место уменьшаемого:

; вычисление Z = X–Y

; X, Y – РПД

; R0 – адрес Y

; R1 – адрес X

; результат на место X

SUBSTR: MOV A,@R0 ; загрузка младшего байта Y

CPL A ; получение дополнительного кода Y

INC A ;

ADD A,@R1 ; вычитание младших байт

MOV @R0,A ; запоминание младшего байта разности

INC R0 ; переход к старшим байтам X и Y

INC R1 ;

MOV A,@R0 ; загрузка старшего байта Y

CPL A ; обратный код Y

ADDC A,@R1 ; вычитание старших байт

MOV @R0,A ; запоминание результата

Умножение двоичных чисел. Пусть производится умножение чисел 1101₂ и 1011₂.

1 1 0 1 множимое

1 0 1 1 множитель

1 1 0 1 1-е частичное произведение

1 1 0 1 2-е частичное произведение

0 0 0 0 3-е частичное произведение

1 1 0 1 4-е частичное произведение

1 0 0 0 1 1 1 1 произведение

Как видно из примера, при выполнении умножения формируются частичные произведения (произведения множимого на цифры разрядов множителя), которые суммируются с соответствующими сдвигами друг относительно друга. В цифровых устройствах процессу суммирования частичных произведений придают последовательный характер: формируется одно из частичных произведений, к нему с соответствующим сдвигом прибавляется следующее частичное произведение, к полученной сумме двух частичных произведений прибавляется с соответствующим сдвигом очередное частичное произведение, и так далее, пока не будут просуммированы все частичные произведения. Этот процесс суммирования можно начинать с младшего либо старшего частичного произведения.

Ниже показаны процессы при умножении с суммированием частичных произведений, начиная со старшего частичного произведения (используется приведенный выше пример умножения чисел 1101₂ и 1011₂).

1 1 0 1 4-е частичное произведение

1 1 0 1 0 сдвиг на один разряд влево

0 0 0 0 3-е частичное произведение

1 1 0 1 0 сумма 4- и 3-го частичных произведений

1 1 0 1 0 0 сдвиг на один разряд влево

1 1 0 1 2-е частичное произведение

1 0 0 0 0 0 1 сумма 4-, 3- и 2-го частичных произведений

1 0 0 0 0 0 1 0 сдвиг на один разряд влево

1 1 0 1 1-е частичное произведение

1 0 0 0 1 1 1 1 произведение

Рассмотрим выполнение операции умножения с суммированием частичных произведений, начиная с младшего частичного произведения на примере умножения чисел 1101₂ и 1011₂.

1 1 0 1 1-е частичное произведение

0 1 1 0 1 сдвиг на один разряд вправо

1 1 0 1 2-е частичное произведение

1 0 0 1 1 1 сумма 1- и 2-го частичных произведений

1 0 0 1 1 1 сдвиг на один разряд вправо

0 0 0 0 3-е частичное произведение

1 0 0 1 1 1 сумма 1-, 2- и 3-го частичных произведений

1 0 0 1 1 1 сдвиг на один разряд вправо

1 1 0 1 4-е частичное произведение

1 0 0 0 1 1 1 1 сумма частичных произведений

1 0 0 0 1 1 1 1 сдвиг вправо, произведение

При умножении целых чисел для фиксации произведения в разрядной сетке должно предусматриваться число разрядов, равное сумме числа разрядов множимого и множителя.

Пример 1.8. Умножить однобайтные целые числа без знака. В регистре R1 размещен множитель, в регистре R2 – множимое. Двухбайтный результат умножения будет размещен в аккумуляторе (старший байт) и в R1 (младший байт) вместо множителя. В регистр R3, выполняющий функции счетчика программных циклов, загружается число 8 (число бит множителя). Умножение выполняется младшими битами вперед со сдвигом вправо частичного произведения. Последовательность действий при этом методе умножения следующая:

– Содержимое аккумулятора и регистра-расширителя R1 сдвигается вправо на один бит так, что младший бит множителя, выдвигаемый из регистра R1, помещается в триггер флага C.

– Если C = 1, то множимое добавляется к содержимому аккумулятора, в противном случае никаких операций не производится.

– Декрементируется счетчик циклов R3, и если его содержимое не равно нулю, то все действия повторяются.

– Перед выходом из подпрограммы формируется окончательный результат сдвигом частичного результата на один бит вправо:

MPL: MOV R3,#8 ; загрузка счетчика циклов

CLR A ; очистка аккумулятора

CLR C ; очистка признака переноса

SHIFT: RRC A ; сдвиг аккумулятора вправо

XCH A,R1 ; обмен аккумулятора и R1

RRC A ; сдвиг множителя с занесением

; выдвигаемого бита в C

XCH A,R1 ; обмен аккумулятора и R1

JNC RESULT ; если C = 1, то суммирование

ADD A,R2 ; прибавление множимого

RESULT: DJNZ R3,SHIFT ; декремент счетчика и проверка

; окончания операции (R3 = 0)

RRC A ; сдвиг аккумулятора

XCH A,R1 ; обмен

RRC A ; сдвиг содержимого R1

XCH A,R1 ; обмен

Пример 1.9. Умножить аккумулятор на число 2 в степени X, где X – число (не более 8), хранящееся в R2. Умножение на 2 заменяется арифметическим сдвигом влево аккумулятора и расширителя R1:

MOV R1,#0 ; сброс R1

CLR С ; сброс флага переноса

LOOP: RLC A ; арифметический сдвиг влево объединенного

XCH A,R1 ; 16-битного результата в

RLC A ; регистровой паре (R1) (A)

XCH A,R1 ;

DJNZ R2,LOOP ; цикл