Навигация
0.231 z + 0.085
---------------------
z^2 - 1.369 z + 0.369
>> sys_tr=d2c(sys,'tustin')
Transfer function:
-0.05332 s^2 - 0.1242 s + 0.4616
--------------------------------
s^2 + 0.9218 s + 2.047e-016
(опция 'tustin’ предназначена для преобразования 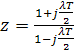 )
)
Получаем выражение:
![]()
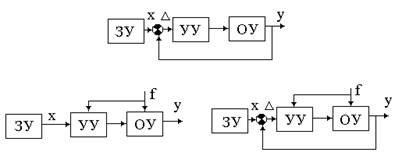
где параметры g и f видны из вышеприведенного выражения.
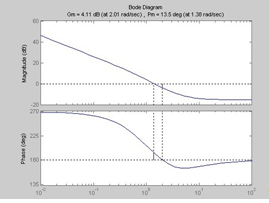
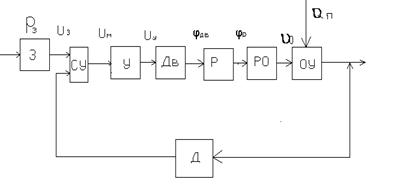
Рис 2.2
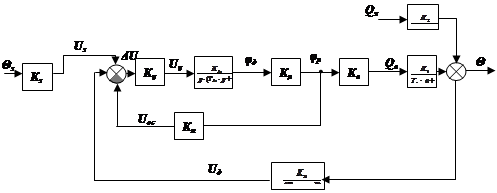
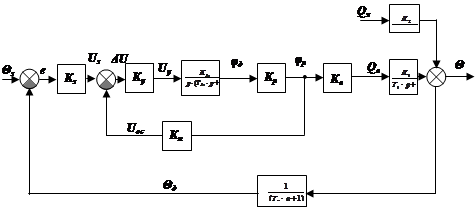
4. Рассматриваемая система для всех вариантов является астатической с астатизмом первого порядка и имеет следующую передаточную функцию:
![]()
![]()
В силу астатизма первого порядка в такой системе статическая ошибка всегда равна нулю, а скоростная еск вычисляется по формуле:
![]()
и следовательно, еск=1,999.
Вычислим коэффициенты ошибок. Величина С0 =0, а коэффициент ошибки
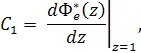
Где ![]() передаточная функция системы по ошибке.
передаточная функция системы по ошибке.
Тогда получим производную:
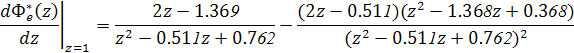
Подставив в последнее выражение найденные ранее значения и z=1, окончательно получим С1=1,999.
5. При входном воздействии вида v(k) = l[k] переходный процесс в замкнутой системе можно вычислить с помощью моделирования импульсной системы в Matlab. Для этого необходимо задать передаточную функцию непрерывной части системы в tf- или zpk -форме, преобразовать ее в дискретную с помощью оператора c2d при заданном времени дискретизации T, а затем построить переходной процесс системы оператором step. Так же можно построить и логарифмические частотные характеристики импульсной системы -bode. Если задана передаточная функция замкнутой системы в виде:
![]()
и периодом дискретизации γT, то получим
>> w0=tf([0.3 1 0],[0.3 1 1.411]) Transfer function:
0.1 s^2 + s
-------------------
0.1 s^2 + s + 3.738
0.2
>> w1=c2d(w0,0.24)
Transfer function:
z^2 - 0.8801 z - 0.1199
------------------------
z^2 - 0.4001 z + 0.09072
Sampling time: 0.24
>> step(W1)

Рис 2.3
На рис.2.4 представлена диаграмма Боде исследуемой дискретной системы с отмеченными на ней запасами устойчивости по амплитуде и фазе.

Рис. 2.4
3.Исследование нелинейной непрерывной системы автоматического управления
Задание:
Используя метод гармонической линеаризации нелинейного элемента, определить на основе частотного способа возможность возникновения автоколебаний в замкнутой системе, их устойчивость, амплитуду и частоту.
Исходные данные:
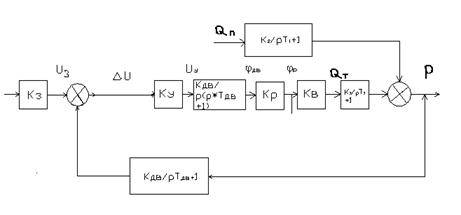
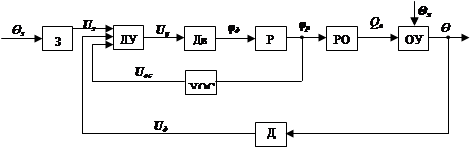
Структура нелинейной САУ представлена на рис. 3.1, где НЭ— нелинейный элемент, W(s) - передаточная функция непрерывной линейной части системы.
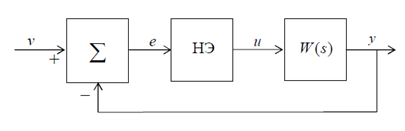
Рис 3.1
1. Передаточная функция W0(s) берется из пункта 1, как передаточная функция скорректированной системы с соответствующими числовыми коэффициентами. Нелинейный элемент НЭ имеет нелинейную характеристику u=f(e) которая для всех заданий является характеристикой идеального реле:
![]()
где с=2.
Приближенная передаточная функция нелинейного элемента для случая идеальное реле имеет вид:
![]()
где a – амплитуда искомого периодического режима, а>0.
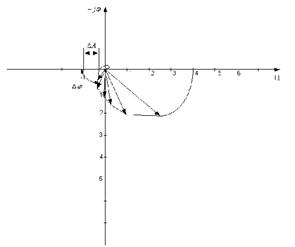
2. На комплексной плоскости строим характеристику:
![]()
Это прямая, совпадающая с отрицательным отрезком действительной оси, вдоль которой идет оцифровка по амплитуде а0 = 0, a1, a2, …. В том же масштабе на комплексной плоскости строится АФЧХ разомкнутой системы W0(jw) при изменении частоты от 0 до + inf.
Передаточная функция скорректированной системы:
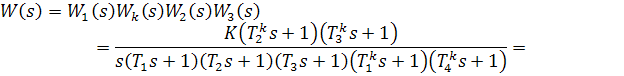
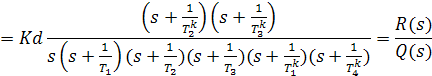
На рис.3.2 (выделен интересующий фрагмент) пунктиром отмечена АФЧХ

рис.3.2
Точка пересечения кривых (-0,165; -0j).
В точке пересечения АФЧХ W0(jw) и прямой ![]() по графику W(jw) находятся частота искомого периодического (гармонического) режима w=w*, а на прямой
по графику W(jw) находятся частота искомого периодического (гармонического) режима w=w*, а на прямой ![]() в точке пересечения его амплитуда а = а*. Тогда в системе существуют периодические колебания:
в точке пересечения его амплитуда а = а*. Тогда в системе существуют периодические колебания:
![]()
Приравнивая Im(W0(jw))=0 находим w*=1,065 (функция fsolve). При найденном значении частоты получим Re(W0(jw*))=-1,3. Из условия Re(W0(jw*))=![]() находим а*=0.41.
находим а*=0.41.
Для определения устойчивости периодического режима можно воспользоваться следующим правилом: если при увеличении амплитуды а вдоль кривой ![]() пересечение АФЧХ W0(jw) происходит «изнутри наружу», то такой периодический режим будет устойчивым, т.е. в системе существуют автоколебания с частотой w* и амплитудой а* .
пересечение АФЧХ W0(jw) происходит «изнутри наружу», то такой периодический режим будет устойчивым, т.е. в системе существуют автоколебания с частотой w* и амплитудой а* .
Таким образом, периодический режим будет устойчивым.
Литература
1. Теория автоматического управления. Конспект лекций: В 2ч. Ч.1:
Линейные непрерывные системы : учеб.-метод. Пособие /В.П.Кузнецов,С.В.Лукьянец,М.А.Крупская.-Мн.:БГУИРб2007.-132с.
2. Кузнецов В.П. Линейные непрерывные системы: Тексты лекций по курсу: Теория автоматического управления.-Мн.:БГУИР,1995.-180с.
3. Электронный учебно-методический комплекс: Теория автоматического управления. Ч.1: Линейные непрерывные системы./ В.П. Кузнецов, С.В. Лукьянец, М.А. Крупская- Мн.:БГУИРб2006.
4. Электронный учебно-методический комплекс: Теория автоматического управления. Ч.2:Дискретные,нелинейные, оптимальные и адаптивные системы /С.В. Лукьянец, А.Т.Доманов,В.П.Кузнецов.М.А.Крупская-Мн.:БГУИР,2007.
5. Кузнецов А.П. Линейные импульсные системы: Математическое описание: Тексты лекций по курсу «Теория автоматического управления»б-Мн.:БГУИР,1996.-70с.
Похожие работы
... значениях функции. Начальное значение функции:. (2.10) Конечное значение функции: . (2.11) 7. Теорема запаздывания . (2.12) 4. Дифференциальные уравнения САУ При математическом описании систем автоматического управления составляют уравнения статики и динамики. Уравнения статики описывают установившиеся режимы и, как правило, являются алгебраическими. Уравнения динамики ...
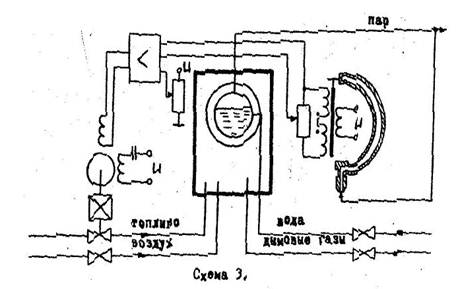
... 10. Общие выводы по работе Литература 1. Цель работы. Задание. Исходные данные Цель работы: закрепление базовых данных и знаний по курсу "Основы автоматики" на примере проведенных анализов системы автоматического регулирования. Задание: 1. Дать краткую характеристику объекта управления, описать устройство и работу системы, составить ее функциональную схему. Сделать вывод о принципе ...
... величины. Для нашей системы статическая ошибка по управляющему воздействию: Статическая ошибка по возмущающему воздействию: По результатам выполнения раздела 8 для САР регулирования температуры поливной воды в теплице можно сделать следующие выводы: Для рассмотренной системы перерегулирование составляет 18,5%, число перерегулирований и колебаний системы за время переходного ...
... можно судить, если в пространстве изменяемых параметров построить область устойчивости, т.е. выделить область значений параметров, при которых система сохраняет устойчивость. Область устойчивости в теории автоматического управления принято называть D – областью, а представление области параметров в виде областей устойчивости и неустойчивости называют D – разбиением. Построение области ...
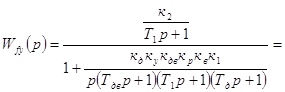

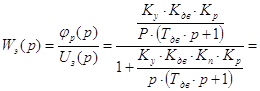
0 комментариев