Навигация
Оценка адекватности построенной модели
3. Оценка адекватности построенной модели
Проверку независимости осуществляем с помощью dw-критерия Дарбина-Уотсона по формуле:
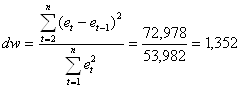
Для вычисления коэффициента Дарбина-Уотсона построим вспомогательную таблицу (8):
Таблица 8
| t |
| Точки поворота |
|
|
| 1 | -2,333 | 5,443 | ||
| 2 | -0,333 | * | 0,111 | 4 |
| 3 | -2,333 | * | 5,443 | 4 |
| 4 | 3,666 | * | 13,440 | 35,988 |
| 5 | 2,666 | * | 7,108 | 1 |
| 6 | 3,666 | * | 13,440 | 1 |
| 7 | -1,333 | 1,777 | 24,99 | |
| 8 | -2,333 | * | 5,443 | 1 |
| 9 | -1,333 | 1,777 | 1 | |
|
| 0 | 6 | 53,982 | 72,978 |
Так как dw попало в интервал от d2 до 2, то по данному критерию можно сделать вывод о выполнении свойства независимости. Это означает, что в ряде динамики не имеется автокорреляции, следовательно, модель по этому критерию адекватна.
Поверку случайности проводим на основе критерия поворотных точек по формуле, количество поворотных точек р при n=9 равно 6:
р>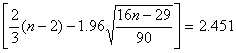
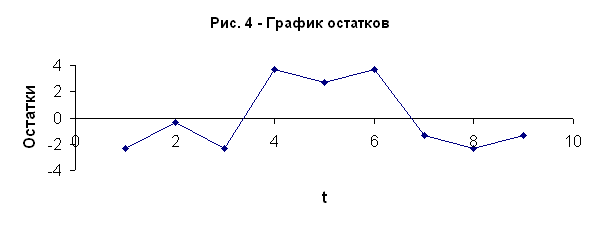
Неравенство выполняется (6>2). Следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.
Соответствие ряда остатков нормальному закону распределения определяем с помощью RS-критерия:
RS=(emax-emin)/S
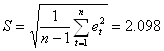
![]()
Расчетное значение RS=2,86 в интервал (2,7 – 3,7) попадает. Следовательно, по данному критерию модель адекватна.
Вывод: модель статистически адекватна.
4) Оценка точности модели
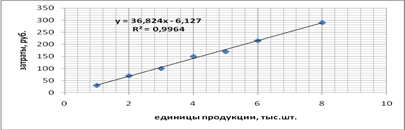
Оценку точности модели проводим на основе использования средней относительной ошибки аппроксимации. Получаем
![]() =5,75%
=5,75%
Вывод: Еотн=5,75% - хороший уровень точности модели.
5) Прогноз спроса на следующие две недели.
Для вычисления точечного прогноза в построенную модель подставляем соответствующие значения фактора t=n+k:
![]()
![]()
Для построения интервального прогноза рассчитываем доверительный интервал. При уровне значимости 0,3, доверительная вероятность равна 70%, а критерий Стьюдента равен 1,119:
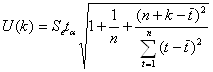
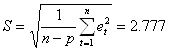
U(1)=3.841,
U(2)=4.065,
Далее вычисляем верхнюю и нижнюю границы прогноза.
Таблица 9
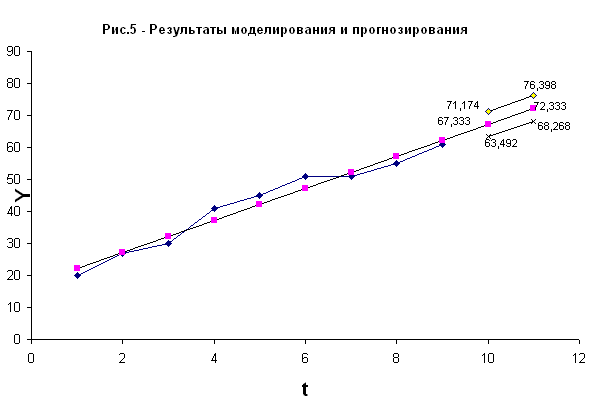
| n+k | U(k) | Прогноз | Верхняя граница | Нижняя граница |
| 10 | U(1)=3,841 | 67,333 | 71,174 | 63,492 |
| 11 | U(2)=4,065 | 72,333 | 76,398 | 68,268 |
6) Графическое представление фактических значений показателя, результатов моделирования и прогнозирования.
Похожие работы
... 807417 6 8,34207 210,6129 Выводы: 1. Решена задача парной регрессии методом наименьших квадратов. 2. Низкая достоверность результатов объясняется рядом причин: - собрано малое количество статистических данных, выбраны случайные районы за небольшой отрезок времени; - в учебных целях добавлены случайные точки, зависящие от порядкового номера студента и числа студентов в группе; - расходы ...
... исходить из вида обрабатываемых данных. В соответствии с современными воззрениями делим эконометрику и прикладную статистику на четыре области: - статистика случайных величин (одномерная статистика); - многомерный статистический анализ; - статистика временных рядов и случайных величин; - статистика объектов нечисловой природы. В первой области элемент выборки - число, во второй - вектор, в ...
... объектов; б) наличие данных за предыдущий период; в) наличие базисных данных; г) сопоставимость данных. 26. По характеру принимаемых решений экономический анализ подразделяется: а) предварительный, текущий и заключительный б) оперативный, ретроспективный и перспективный в) предварительный, последующий и итоговый 27. Информация, ...
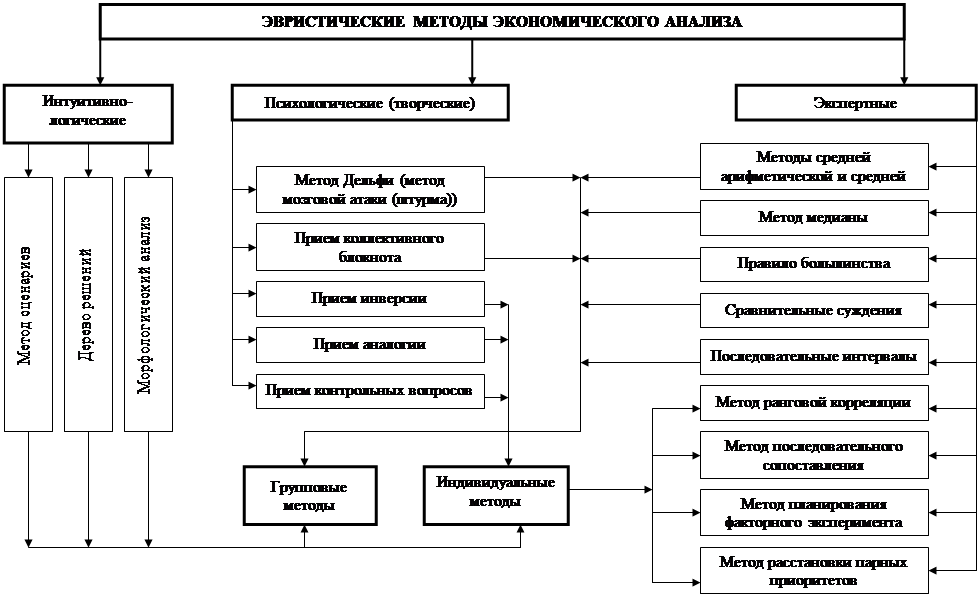
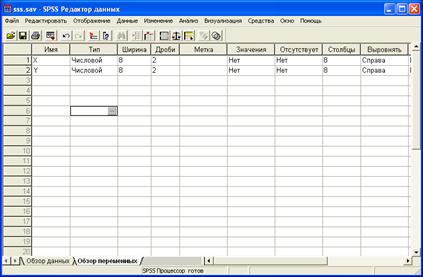
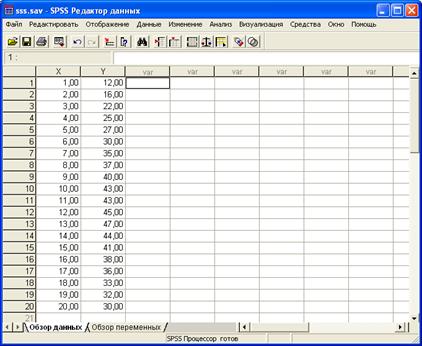
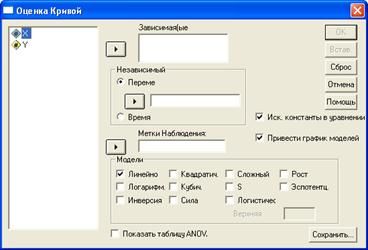
... а также любые колебания, в которых прослеживается закономерность. В качестве примера можно назвать модель экспоненциального сглаживания Брауна. 3. Пример проведения прогнозирования прибыли с использованием пакета SPSS Постановка задачи: Необходимо построить модель, дающую возможность предсказывать размер прибыли некоторой торговой фирмы, если известны данные о ежемесячной прибыли за последние ...

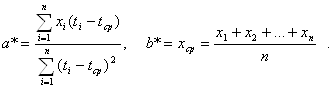
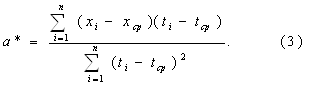


0 комментариев