Трудности в измерении данных (присутствуют ошибки измерений), а также ошибка образуется при округлении расчетных значений

2.  Трудности в измерении данных (присутствуют ошибки измерений), а также ошибка образуется при округлении расчетных значений.

Ход измерения данного показателя во временном ряде связывают не с фактором, а с течением времени, что проявляется в образовании одномерных временных рядов.

Кроме полиномиальных кривых роста одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической нелинейной функции, характеризующей зависимость ряда от времени. Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения эконометрических моделей спроса и предложения чаще всего используют экспоненциальный тренд: .

Поскольку мы рассмотрели уже достаточно много моделей, по которым можно строить прогнозы спроса и предложения в зависимости от времени, то необходимо определить какая из них будет лучше анализировать исходный параметр, т.е. определить тип тенденции.

Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих целях можно использовать и коэффициент автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанные по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни yt и yt-1 тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанные по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.

Возможен случай еще одной модели - степенной, имеющей вид:

Перейдем к анализу параметров модели в нелинейных трендах. Все они могут быть получены с помощью метода наименьших квадратов, если нелинейную модель привести к линейному виду. Так экспоненциальный тренд будет иметь вид: . Отсюда находим a и b:

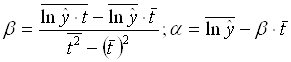
Обратным переходом найдем параметры а и b.

Для степенной модели имеем вид: . Для нахождения параметров a и b решаем систему нормальных уравнений:

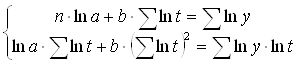
Зависимость спроса и предложения от времени часто не ярко выражена. Лучшей для анализа этих явлений будут модели так называемой множественной регрессии, в которых спрос или предложение зависят от многих факторов. Такие модели чаще применяются поскольку позволяют прогнозировать значения показателя при изменении того или иного фактора.

Например, предположим спрос на картофель (показатель y) зависит от заработной платы (фактор х₁), времени года (фактор х₂), места расположения области (фактор х₃), накоплений населения в банках (фактор х₄), уровня инфляции в месяц (фактор х₅). Некоторые факторы можно принять за числовые значения, например времена года: зима - 2, весна - 2,5, лето - 3, осень - 3,5 (или по месяцам). Тогда можно построить многофакторную модель регрессии: . Такая модель будет ярко показывать что произойдет со спросом на картофель, если изменится заработная плата, и (или) инфляция и т.д.

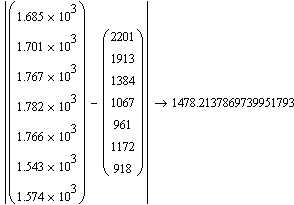
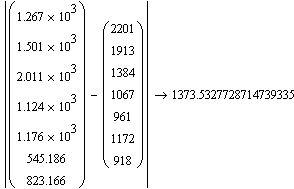
Для нахождения параметров модели используют либо метод наименьших квадратов, либо матричную запись.

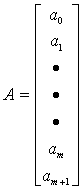
Матрица Х - показывает факторы, матрица Y - показатель, матрица А - коэффициенты регрессии.

; ;

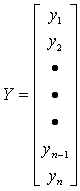Таким образом, уравнение множественной регрессии примет вид: .

С помощью элементарных действий над матрицами найдем выражение матрицы А: , где X’ - транспонированная матрица Х.

В теории спроса и предложения могут встречаться не только линейные или нелинейные модели. Многие экономисты выводят различные зависимости между спросом и переложением. Например, существует эконометрические модель спроса и предложения кейнсианского типа, построенная на системе совместных, одновременных уравнениях.

где  - спрос на товар в момент времени t;

 - предложение на товар в момент времени t;

 - цена товара в момент времени t;

 - доход в момент времени t;

 - цена товара в предыдущий период.

Система совместных, одновременных уравнений (или структурная модель) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные обозначены в приведенной системе одновременных уравнений как Q. Это зависимые переменные, число которых равно числу уравнений в системе [2, c.136].

Экзогенные переменные - все остальные. Это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.

Структурная форма такой модели позволяет увидеть влияние любой экзогенной переменной на значение эндогенной переменной. Меняя цены на товары и доходы, можно заранее иметь целевые значения спроса и потребления.

При анализе покупательского спроса широко применяются однофакторные функции спроса от дохода. Соответствующие этим функциям кривые  (Z - доход) называются кривыми Энгеля. Формы этих кривых для различных товаров могут быть различны. Если спрос на данный товар возрастает примерно пропорционально доходу, то функция будет линейной. Такой характер имеет, например, спрос на одежду, фрукты и др. кривая Энгеля для этого случая представлена на рисунке 1.

Если по мере роста дохода спрос на данную группу товаров возрастает все более высокими темпами, то кривая Энгеля будет выпуклой (рис.2). Так ведет себя спрос на предметы роскоши.

Если рост значений спроса, начиная с определенного момента, по мере насыщения спроса отстает от роста дохода, то кривая Энгеля будет иметь вид вогнутой кривой (рис.3). Например, такой характер имеет спрос на товары первой необходимости.

Тот же принцип разграничения групп товаров по типам функции спроса от дохода использовал шведский экономист Л. Торнквист, который предложил специальные виды функций спроса (функции Торнквиста) для трех групп товаров: первой необходимости, второй необходимости, предметов роскоши.

Функция Торквиста для товаров первой необходимости имеет вид:

и отражает тот факт, что рост спроса на эти первоочередные товары с ростом дохода постепенно замедляется и имеет предел а1 (кривая спроса асимптотически приближается к прямой линии у = а1). График функции является вогнутой кривой I на рисунке 4.

Функция спроса по Торнквисту на товары второй необходимости выражается формулой:

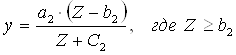
Эта функция также имеет предел а2, но более высокого уровня; при этом спрос на эту группу товаров появляется лишь после того, как доход достигнет величины b2; график функции - вогнутая кривая II на рисунке 4.

Наконец, функция Торнквиста для предметов роскоши имеет вид:

Эта функция не имеет предела. Спрос на эти товары возникает после того, как доход превысит величину b3, и далее быстро возрастает, так что график функции - выпуклая кривая III на рисунке 4.

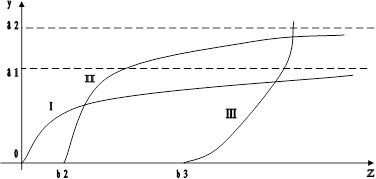
Рисунок 4

Кроме указанных функций, в аналитических моделях покупательского спроса используются также другие функции, например S-образные. Не ограничивается и число функций или моделей по которым можно описывать и прогнозировать предложение. В большинстве случаев все модели, построенные по некоторым имеющимся данным очень индивидуальны, на одни товары может хорошо выявлять тенденцию степенная модель, на другие полиномиальная, на третьи экспоненциальная и очень много других вариантов.

Список использованной литературы

1. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учеб. - 5-е изд., испр. - М.: Дело, 2001. - 400 с.

2. Эконометрика: Учебник / Под ред.И. И. Елисеевой. - М.: Финансы и статистика, 2002. - 344 с.: ил.

3. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курдышева, Н.М. Гордеенко и др.; Под ред.И. И. Елисеевой. - М.: Финансы и статистика, 2002. - 192 с.: ил.

4. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. - М.: ЮНИТИ, 2002. - 391 с.