Любая из точек локального минимума унимодальной функции является и точкой ее глобального минимума на отрезке [а; b]
Пример решения методами дихотомии и золотого сечения
Численные методы многомерной безусловной оптимизации
Поиск точки min методом циклического покоординатного спуска
Основы линейного программирования
Навигация
Численные методы многомерной безусловной оптимизации
Сравнительный анализ методов оптимизации
22076
знаков
78
таблиц
12
изображений
3. Численные методы многомерной безусловной оптимизации
Рассмотрим конкретные вычислительные алгоритмы решения задачи безусловной минимизации f (х) ® min, xÎ En, которые опираются только на вычисление значений функции f (х), т.е. прямые методы минимизации. Важно отметить, что для их применения не требуется дифференцируемость целевой функции и даже ее аналитическое задание. Нужно лишь иметь возможность вычислять или измерять значения f (х) в произвольных точках. Такие ситуации часто встречаются в практически важных задачах оптимизации.
3.1 Поиск точки min методом правильного симплекса
В пространстве E2 правильным симплексом является совокупность вершин равностороннего треугольника, в E3 – правильного тетраэдра.
Если х0 – одна из вершин правильного симплекса в En то координаты остальных n вершин х1 ,..,хn можно найти, например, по формулам:
(3.1)
где d1
, d2
, a– длина ребра. Вершину х0 симплекса, построенного по формулам (3.1), будем называть бaзовой.
По известному симплексу можно построить новый симплекс отрaжением какой–либо вершины, например, хk симметрично относительно центра тяжести хc остальных вершин симплекса.
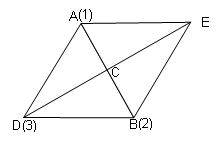
Пусть задана функция f(x,y) ® min и начальный базис (x0,y0).
Новая и старая вершины связаны соотношением:
, где xc
, где уc
(3.2)
Вычисляем значение функции в точках f(A), f(B), f(D) (пусть f(A)<f(B)<f(D)) и присваиваем им номера в порядке возрастания A-1, B-2, D-3.
Вершину с наибольшим номером отражаем относительно центра тяжести стороны 1-2
Координаты вершины Е:
(3.3)
Затем вычисляем f(E) и сравниваем f(E) и f(D). Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. В противном случае выполняют еще одну попытку отражения для вершины со следующим по величине значением f (х). Если и она не приводит к уменьшению функции, то сокращают длину ребра симплекса, например, вдвое и строят новый симплекс с этим ребром. В качестве базовой выбирают ту вершину х0 старого симплекса, в которой функция принимает минимальное значение. Поиск точки минимума f (x) заканчивают, когда либо ребро симплекса, либо разность между значении функции в вершинах симплекса становятся достаточно малыми.
3.2 Поиск точки min методом деформируемого симплекса
Алгоритм, описанный выше, можно модифицировать, добавив к процедуре отражения при построении нового симплекса процедуры сжатия и растяжения. Положение новой вершины находится сравнением и выбором наименьшего среди значений целевой функции в точках;
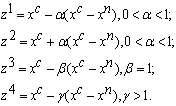(3.5)
Так как величина a Î (0; 1), то выбор точек z1 и z2 соответствует сжатию симплекса; b » 1, поэтому выбор точки z3 соответствует отражению, а g > 1 и выбор точки z4 приводит к растяжению симплекса. На практике хорошо зарекомендовал себя следующий набор параметров a, b и g для выбора пробных точек zi: a = 1/2, b = 1 и g =2.
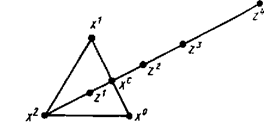
Рис. 3.2. Пробные точки z1,z2,z3,z4 для перехода к новому симплексу
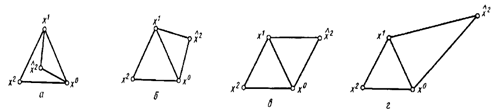
Рис. 3.3. Новые симлексы полученные в результате процедур сжатия (а,б); отражения (в); растяжения(г).
Опишем алгоритм метода поиска точки минимума функции по деформируемому симплексу.
Шаг 0 – Шаг 3 Аналогичны методу правильного симплекса.
Шаг 4. Найти 
и пробные точки zk , k=1, …, 4 пo формулам (3.5). Найти f (z*)= min f (zk). Если f (z*) < f (zn). то положить xn=z* и перейти к шагу 2. Иначе – перейти к шагу 5.
Похожие работы
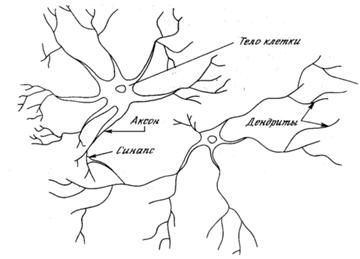
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
... с издержками двух или трех конкурентов. Это позволит выявить конкурентоспособность предприятия, определить имеющиеся резервы для снижения издержек. Подобный сравнительный анализ издержек производства на данном предприятии и предприятиях-конкурентах служит основанием для разработки и проведения стратегических мероприятий по снижению издержек производства и оптимизации производственной программы. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... ) аппарат, а затем полученную величину корректируют с учетом других факторов (долгосрочная стратегия предприятия, ограничения по производственным мощностям и пр). 3. Рекомендации по оптимизации величины себестоимости продукции на основе анализа соотношения "затраты - объем - прибыль" 3.1 Деление затрат на постоянные и переменные части и определение показателей маржинального дохода ...
0 комментариев