Навигация
Поиск точки min методом циклического покоординатного спуска
3.3 Поиск точки min методом циклического покоординатного спуска
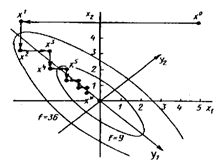
Этот метод заключается в последовательной минимизации целевой функции f (x) сначала по направлению первого базисного вектора е1, затем второго – е2 и т.д. После окончания минимизации по направлению последнего базисного вектора еn цикл повторяется.
Опишем этот алгоритм.
Шаг 0. Выбрать х Î En , критерий достижения точности, величину e. Найти f (x), положить j= 1.
Шаг 1. Решить задачу одномерной минимизации Ф(a) = f (х + aеj)® min, a Î R, т.е. найти a*. Положить ![]() = х +a*еj, вычислить f (х).
= х +a*еj, вычислить f (х).
Шаг 2. Если j < п, то положить х =![]() , j=j+1 и перейти к шагу 1, иначе – перейти к шагу 3.
, j=j+1 и перейти к шагу 1, иначе – перейти к шагу 3.
Шаг 3. Проверить условие достижения точности ||х–![]() || < e
|| < e
3.4 Поиск точки min методом Хука – Дживса
Этот алгоритм содержит две основные процедуры:
а) исследующий покоординатный поиск в окрестности данной точки, предназначенный для определения направления убывания f (х);
б) перемещение в направлении убывания.
Опишем алгоритм исследующего покоординатного поиска из заданной точки х с приращениями по каждой координате Dj , j = 1, …, n
Шаг 1. Положить ![]() = x , i = 1.
= x , i = 1.
Шаг 2. Сделать пробный шаг y=![]() – Dje j, где e j –j–й базисный вектор. Если f (
– Dje j, где e j –j–й базисный вектор. Если f (![]() ) £ f (y), то перейти к шагу 3, иначе – к шагу 4.
) £ f (y), то перейти к шагу 3, иначе – к шагу 4.
Шаг 3. Сделать пробный шаг y=![]() +Dje j . Если f (
+Dje j . Если f (![]() ) £ f (y), то перейти к шагу 5, иначе – к шагу 4.
) £ f (y), то перейти к шагу 5, иначе – к шагу 4.
Шаг 4. Положить ![]() = у.
= у.
Шаг 5. Положить j = j + 1. Если j £ n, то перейти к шагу 2. В противном случае исследующий поиск окончен – получена точка ![]() для которой f (
для которой f (![]() ) < f (y), если
) < f (y), если ![]() ¹ х.
¹ х.
3.5 Пример решения методами правильного симплекса, деформируемого симплекса, покоординатного спуска, Хука – Дживса
Дана функция ![]() , с=7; d=7.
, с=7; d=7.
Найти минимум функции с точностью ε=0,001
Метод правильного симплекса
Выбираем длину стороны треугольника l=10ε=0,0001
Вершины треугольника находим следующим образом:
A(![]() );
);
B(![]()
![]() );
);
D(![]()
![]() ).
).
A(1,065; 0,918);
B(1,07,0,927);
D(1,075,0,918).
Шаг 0
F(A)=10,903; F(B)=11,081; F(D)=11,051.
F1<F2<F3:
F1=F(A); F2=F(D); F3=F(B).
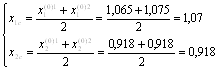
Отражаем вершину 3 относительно центра тяжести.
![]()
F(E)=10,873.
Значение функции в найденной точке меньше, значения функции в точке 1, поэтому принимаем новый симплекс (1,2,E).
Шаг 1
F(1)=10,903; F(2)=11,081; F(E)=10,873.
F1<F2<F3:
F1=F(E); F2=F(1); F3=F(2).
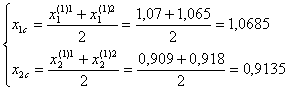
Отражаем вершину 3 относительно центра тяжести.
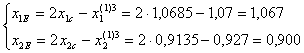
F(E)=10,726.
Значение функции в найденной точке меньше, значения функции в точке 1, поэтому принимаем новый симплекс (1,2,E).
![]() ,
,
![]() .
.
В результате получаем x1=0,125, x2=0,208, f(x1, x2)=-0,41.
Метод деформируемого симплекса
Выбираем длину стороны треугольника l=5ε=0,005
Вершины треугольника находим следующим образом:
A(![]() );
);
B(![]()
![]() );
);
D(![]()
![]() ).
).
A(1,065; 0,918);
B(1,07,0,927);
D(1,075,0,918).
Принимаем коэффициенты выбора пробных точек k1=0,5, k2=1, k3=2.
Шаг 0
F(A)=10,903; F(B)=11,081; F(D)=11,051.
F1<F2<F3:
F1=F(A); F2=F(D); F3=F(B).
Находим центр тяжести вершины 3 относительно вершин 1 и 2:
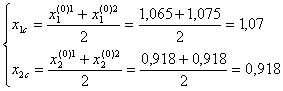
Выбираем пробные точки:
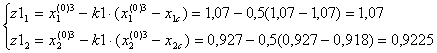
F(z1)=10,966.
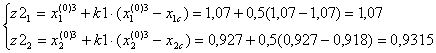
F(z2)=11,018.
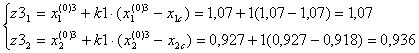
F(z3)=11,044.
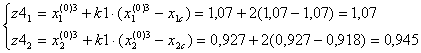
F(z3)=11,097.
Значение функции в z1 точке меньше, значения функции в точке 3, поэтому принимаем новый симплекс (1,2,z1).
Шаг 1
F(1)= 10,903; F(2)= 11,051; F(z1)=10,966.
F1<F2<F3:
F1=F(1); F2=F(z1); F3=F(2).
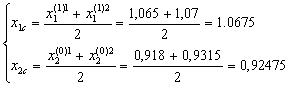
Выбираем пробные точки:
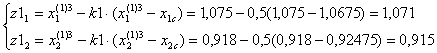
F(z1)=10,955.
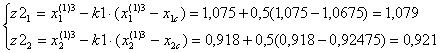
F(z2)=10,998.
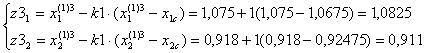
F(z3)=11,019.
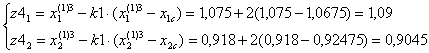
F(z3)=11,062.
Значение функции в точке z1 меньше, значения функции в точке 3, поэтому принимаем новый симплекс (1,2,z1).
![]() ,
,
![]() .
.
В результате получаем x1=-0,012, x2=0,419, f(x1, x2)=-0,014.
Метод покоординатного спуска
(1,065; 0,918).
![]()
α=5ε=0,005.
Шаг 1
Координату ![]() закрепляем,
закрепляем,
![]()
![]()
Т.к.![]()
![]() ,
,
Следовательно ![]()
![]()
![]()
![]()
![]()
![]()
Получим x1=0,012, ![]()
Шаг 2
Принимаем ![]() и закрепляем,
и закрепляем,
![]()
![]()
Т.к.![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
Получим x2=0,199, ![]()
Продолжаем поиск до тех пор, пока не будет выполнено условие ![]()
В результате получаем x1=0,117, x2=0,189, f(x1, x2)=-0,411.
Метод Хука-Дживса
x0: (1,065; 0,918).
![]()
Δ1=5*ε=5*0,001, Δ2=5*ε=5*0,001.
λ=2.
Шаг 1
Принимаем k1=-1, k2=-1 – коэффициенты, определяющие направление поиска.
![]()
![]()
![]()
В данном направлении функция убывает.
Шаг 2
Принимаем k1=-1, k2=-1.
![]()
![]()
![]()
В данном направлении функция убывает.
Продолжаем поиск до тех пор, пока не будет выполнено условие ![]()
В результате получаем x1=0,115, x2=0,198, f(x1, x2)=-0,411.
Похожие работы
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
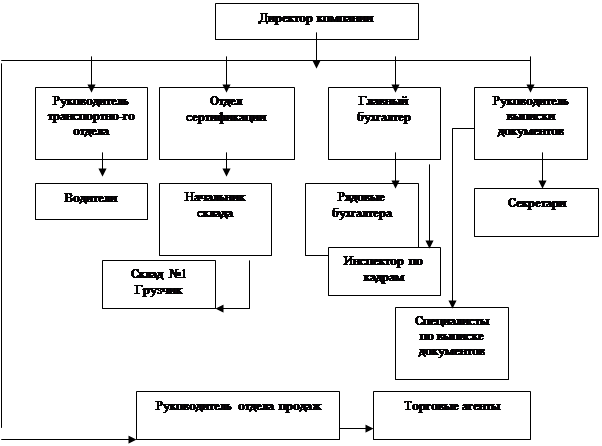
... с издержками двух или трех конкурентов. Это позволит выявить конкурентоспособность предприятия, определить имеющиеся резервы для снижения издержек. Подобный сравнительный анализ издержек производства на данном предприятии и предприятиях-конкурентах служит основанием для разработки и проведения стратегических мероприятий по снижению издержек производства и оптимизации производственной программы. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... ) аппарат, а затем полученную величину корректируют с учетом других факторов (долгосрочная стратегия предприятия, ограничения по производственным мощностям и пр). 3. Рекомендации по оптимизации величины себестоимости продукции на основе анализа соотношения "затраты - объем - прибыль" 3.1 Деление затрат на постоянные и переменные части и определение показателей маржинального дохода ...

0 комментариев