Навигация
1. Теоретична частина
1.1 Постановка задачі
Системи лінійних рівнянь.
Розв’язком деякої множини (системи) рівнянь
F1 (x1, x2, …, xn) = 0, …, Fm (x1, x2, …, xn) = 0
з невідомими x1, x2, …, xn називається множина значень невідомих, які перетворюють одночасно всі рівняння системи в тотожності. Система рівнянь вважається розв’язаною, якщо знайдено всі такі значення невідомих або доведено, що не існує набору значень невідомих, які перетворювали б одночасно всі рівняння системи в тотожності. В останньому випадку кажуть, що система не має розв’язків або що вона несумісна.
Систему рівнянь часом записують, об’єднуючи рівняння фігурною дужкою.
Дві системи рівнянь вважають еквівалентними, якщо вони мають одну й ту саму множину розв’язків. (Дві несумісні системи за означенням вважаються еквівалентними.)
Кажуть, що система рівнянь (S) еквівалентна двом системам рівнянь (S1) і (S2), якщо множина розв’язків системи (S) збігається з об’єднанням множин розв’язків систем (S1) і (S2).
Властивості систем рівнянь:
1) При заміні будь-якого рівняння системи еквівалентним рівнянням утворюється еквівалентна система.
2) Якщо одне з рівнянь системи (S) еквівалентне деяким двом рівнянням, то початкова система (S) еквівалентна двом системам (S1) і (S2), в кожній з яких це рівняння замінене на одне з рівнянь еквівалентної сукупності, а решта залишена без змін.
Системою s лінійних алгебраїчних рівнянь з n невідомими x1, x2, …, xn називається система вигляду
a11x1 + a12x2 +…+ a1nxn = b1,
a21x1 + a22x2 +…+ a2nxn = b2,
. . . . . . . . . . . . . . . . . . . . . .
as1x1 + as2x2 +…+ asnxn = bs.
Величини a11, a12, …, a1n, a21, a22, …, a2n, …, as1, as2, …, asn називаються коефіцієнтами даної лінійної системи рівнянь. Індекси біля коефіцієнтів лінійної системи означають: перший індекс показує номер рівняння системи, другий індекс показує номер невідомого, при якому стоїть даний коефіцієнт. Так, наприклад, a25 – коефіцієнт, що стоїть у другому рівнянні системи при невідомому х5.
Величини b1, b2, ..., bs називаються вільними членами першого, другого, ..., s-го рівнянь системи. Система рівнянь називається однорідною, якщо всі числа bj дорівнюють нулю (j=1, 2, 3, ..., s), і неоднорідною, якщо хоча б одне bj відмінне від нуля.
Упорядкована множина n чисел k1, k2, k3, …, kn називається розв’язком системи, якщо при підстановці його в систему замість невідомих x1, x2, x3, …, xn усі рівняння системи перетворюються в тотожність. Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку.
Сумісна система лінійних рівнянь називається визначеною, якщо вона має єдиний розв’язок, тобто існує тільки один набір n чисел k1, k2, k3, …, kn, який перетворює всі рівняння системи в тотожності.
Сумісна система лінійних рівнянь називається невизначеною, якщо розв’язків більше ніж один.
Система однорідних рівнянь завжди має нульовий розв’язок:
x1 = x2 = x3 = … = xn = 0
Якщо система однорідних рівнянь має ненульовий розв’язок k1, k2, k3,..., kn (тобто хоча б одне з чисел ki (i = 1 ,2,…, n) відмінне від нуля), то така система має і незліченну множину розв’язків вигляду lk1, lk2, …, lkn, де l - будь-яке число.
1.2 Розв’язання системи лінійних рівнянь методом Гаусса
Одним з найпоширеніших методів розв’язування систем алгебраїчних рівнянь є метод послідовного виключення невідомих – метод Гаусса. Цей метод ґрунтується на деяких перетвореннях системи лінійних рівнянь, внаслідок яких дістанемо систему, еквівалентну початковій системі.
Метод Гаусса ґрунтується на деяких перетвореннях системи лінійних рівнянь, внаслідок яких дістанемо систему, еквівалентну початковій системі.
Алгоритм гауссових вилучень полягає у послідовному застосуванні до системи таких елементарних перетворень:
1) множення рівняння системи на число, відмінне від нуля;
2) додавання до одного рівняння іншого, помноженого на довільне число;
3) зміна місцями двох рівнянь в системі.
Після елементарних перетворень система стає рівносильною. Якщо система лінійних рівнянь має вигляд
a11x1 + a12x2 +…+ a1nxn = b1,
a22x2 +…+ a2nxn = b2,
…………………………….
annxn = bn,
тобто матриця коефіцієнтів системи – верхня трикутна, то розв’язують її досить просто, послідовно виключаючи невідомі по черзі з останнього рівняння.
Прямий перебіг методу Гаусса саме й дає змогу внаслідок елементарних перетворень замінити систему лінійних рівнянь загального вигляду еквівалентною системою з верхньою трикутною матрицею.
Є багато реалізацій методу Гаусса з певними перевагами обчислення. Наприклад, у схемі з вибором головного елемента послідовність вилучення визначають під час обчислення.
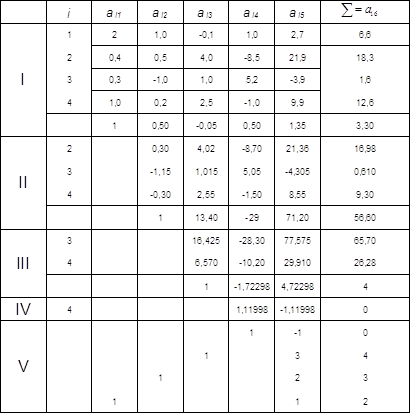
Схема єдиного ділення. Опишемо метод Гаусса для розв’язування системи лінійних рівнянь загального вигляду:
a11x1 + a12x2 +…+ a1nxn = a1,n+1,
a21x1 + a22x2 +…+ a2nxn = a2,n+1,
...................................................
an1x1 + an2x2 +…+ annxn = an,n+1.
Виберемо a11
Похожие работы
... . Отже, . 2.3 Опис та інструкція по використанню програми Gauss Дана програма реалізована в інтегрованому середовищі програмування Visual Studio 2008 SP1 мовою програмування С#. Вона дозволяє розв’язувати систему лінійних алгебраїчних рівнянь методом Гауса, записаних в матричній формі, а також методом з пошуком головного елемента, при чому матриці можуть будь-якою вимірністю mxn (m і n – кі ...
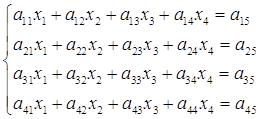
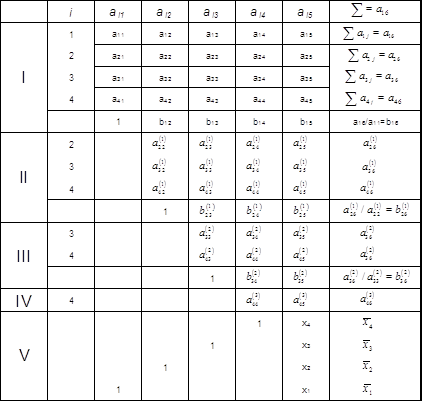
0 комментариев