Навигация
2.3 Контрольний приклад
Схема єдиного ділення.
Продемонструємо алгоритм гауссових вилучень на прикладі:
2x1 + 4x2 + 6x3 + 8x4 = 2,
3x1 + 5x2 + 6x3 + 13x4 = 8,
5x1 + 10x2 + 16x3 + 19x4 = 3,
7x1 + 12x2 + 20x3 + 27x4 = 9.
Випишемо розширену матрицю системи, відокремивши стовпчик вільних членів від коефіцієнтів біля невідомих вертикальною рискою:

Коефіцієнт 2 біля x1 у першому рівнянні назвемо провідним.
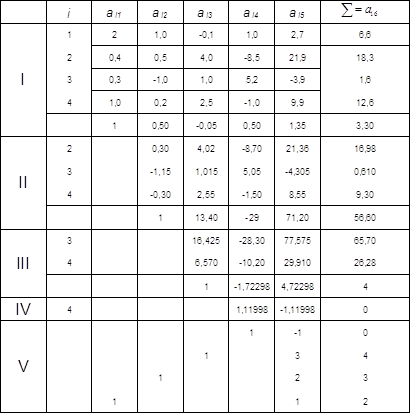
Перший крок методу Гаусса полягає у вилучення змінної з другого, третього та четвертого рівнянь системи. Для цього поділимо коефіцієнти першого рівняння на провідний елемент:

Додамо до другого перше рівняння, помножене на -3; до третього – перше, помножене на -5; до четвертого – перше, помножене на -7. Дістанемо еквівалентну систему рівнянь з розширеною матрицею:

На другому кроці вилучимо змінну x2 з третього та четвертого рівнянь. Провідним елементом виберемо коефіцієнт -1 біля x2 у другому рівнянні.
Поділимо на -1 коефіцієнти другого рівняння:

У третьому рівнянні змінної x2 немає, тому залишаємо його без змін. Помножимо друге рівняння на 2 і додамо його до четвертого:
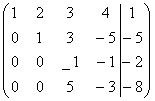
На третьому кроці провідний елемент (коефіцієнт біля x3 у третьому рівнянні) дорівнює 1. залишаємо це рівняння без змін. З четвертого рівняння вилучимо змінну x3, помноживши третє рівняння на -5 і додавши його до четвертого:

Поділивши останнє рівняння на 2 одержимо: x4=1. На цьому прямий перебіг методу Гаусса завершено. Зворотний перебіг полягає в послідовному знаходженні невідомих з перетвореної системи. За значенням x4 з третього рівняння знаходимо: x3=-2+ x4=-2+1=-1 і, нарешті, з першого рівняння:
x1=1-2x2-3x3-4x4=1+2+3-4=2. Перевіривши, переконуємося, що знайдені значення невідомих перетворюють кожне рівняння в тотожність.
Відповідь: система має єдиний розв’язок: x1=2, x2=-1, x3=-1, x4=1.
Висновок
Однією з головних задач лінійної алгебри є розв’язання систем лінійних алгебраїчних рівнянь – математичної моделі реальних об’єктів, залежності між параметрами яких мають лінійний характер. У багатьох фізичних задачах електро-, радіотехніки, механіки баланс сил, діючих на якусь конструкцію, моделюють системою лінійних рівнянь. Наприклад, баланс сил струмів у вузлах і напруг у контурах електричного кола на підставі законів Кірхгофа описують системою рівнянь, лінійних відносно опорів та джерел енергії. Фізичні системи, модельовані диференціальними рівняннями, які не завжди можна розв’язати в аналітичному вигляді, описують наближено системою різницевих рівнянь. До лінійних систем зводяться також задачі статистики, економіки тощо.
Системи лінійних алгебраїчних рівнянь розв’язують точними (прямими) й наближеними методами.
Серед точних методів найвідомішим та найефективнішим є метод Гаусса, чи метод послідовного вилучення невідомих. Цей алгоритм був знаний ще в давнину, принаймні в III ст. до н. е.
Метод Гаусса розв’язування систем лінійних рівнянь з числовими коефіцієнтами завдяки простоті і однотипності виконуваних операцій придатний для використання на електронно-обчислювальних машинах. Істотним недоліком цього методу є неможливість сформулювати умови сумісності і визначеності системи залежно від значень коефіцієнтів і вільних членів. З іншого боку, навіть для визначеної системи цей метод не дає змоги знайти загальні формули, що визначають розв’язки системи через її коефіцієнти і вільні члени, які необхідно мати для теоретичних досліджень. Існують й інші методи розв’язування і дослідження систем лінійних рівнянь, які не мають зазначених недоліків. Ці методи ґрунтуються на теорії матриць і визначників.
Корені лінійних систем алгебраїчних рівнянь за методом Гаусса на сучасних ЕОМ обчислюють за спеціальними стандартними програмами. Такі програми записують різними мовами програмування.
В даному курсовому проекті розроблено та описано програму отримання результатів розв’язку системи алгебраїчних рівнянь методом Гаусса мовою програмування Turbo Pascal. Програма відсаджена з використанням набору текстових даних. Контрольний приклад розроблений вручну для перевірки роботоздатності програми. Він повністю співпав з результатом машинного експерименту. Тому дану програму можна використовувати на практиці.
Запуск програми здійснюється з головного меню інтегрованого середовища Turbo Pascal ( шляхом вибору опції RUN). Попередньо програма повинна бути завантажена в оперативну пам'ять. Можна було б відкомпілювати дану програму з опцією Destination to Memory для запуску exe – файла. Тож можна зробити висновки про можливість вдосконалення цієї програми.
Список використаної літератури
1. „Інформатика. Комп’ютерна техніка. Комп’ютерні технології”/ Підручник. За редакцією О.І. Пушкаря. – Київ. Видавничий центр „Академія”, (Навчальне видання. Серія „Альма-матер”. Заснована в 1999 році.) 2002. – 703с.
2. О.Г. Ципкін „Довідник з математики для середніх навчальних закладів” / За редакцією С.О. Степанова. – К.: Вища школа. Головне вид-во, 1988. – 416с.
3. В.Я. Сердюченко „Розробка алгоритмів та програмування мовою Turbo Pascal”.
Додатки
Результат машинного експерименту
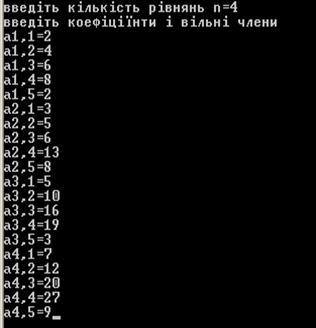
(******************************)
* Програма розв'язку *
* системи лінійних рівнянь *
* методом Гауса *
(******************************)
{01} program kyrsova;
{02} uses crt;
{03} type
{04} mas1=array[1..50,1..51] of real;
{05} mas2=array[1..50] of real;
{06} var
{07} a:mas1;
{08} x:mas2;
{09} b,c,d,r:real;
{10} i,j,n,k,m:integer;
(* Процедура вводу коефіцієнтів і вільних членів *)
{11} procedure vvid(var n:integer; var a:mas1);
{12} begin
{13} write('введіть кількість рівнянь n=');
{14} readln(n);
{15} writeln('Введіть коефіцієнти і вільні члени');
{16} for i:=1 to n do
{17} for j:=1 to n+1 do
{18} begin
{19} write('a',i,',',j,'=');
{20} readln(a[i,j]);
{21} end;
{22} end;
(* Процедура зміни рівнянь місцями *)
{23} procedure mriv(var a:mas1);
{24} begin
{25} if a[k,k]=0 then
{26} for m:=1 to n do
{27} begin
{28} for i:=k to k do
{29} for j:=k to n+1 do
{30} begin
{31} r:=a[i,j];
{32} a[i,j]:=a[i+1,j];
{33} a[i+1,j]:=r
{34} end;
{35} end;
{36} end;
(*Процедура ділення рівняння на провідний коефіцієнт *)
{37} procedure dil(var a:mas1);
{38} begin
{39} b:=a[k,k];
{40} for i:=k to k do
{41} for j:=k to n+1 do
{42} a[i,j]:=a[i,j]/b;
{43} end;
(* Процедура обчислення нових коефіцієнтів *)
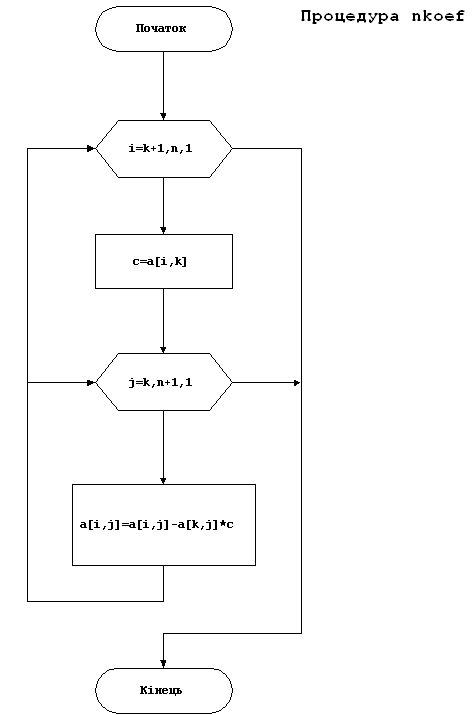
{44} procedure nkoef(var a:mas1);
{45} begin
{46} for i:=k+1 to n do begin
{47} c:=a[i,k];
{48} for j:=k to n+1 do
{49} a[i,j]:=a[i,j]-a[k,j]*c;
{50} end;
{51} end;
(* Процедура обчислення коренів рівняння *)
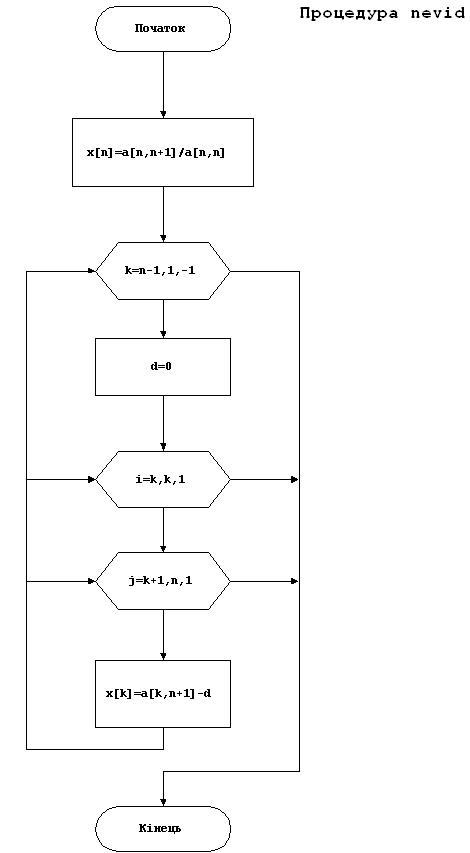
{52} procedure nevid(var x:mas2);
{53} begin
{54} x[n]:=a[n,n+1]/a[n,n];
{55} for k:=n-1 downto 1 do begin
{56} d:=0;
{57} for i:=k to k do
{58} for j:=k+1 to n do
{59} d:=d+a[k,j]*x[j];
{60} x[k]:=a[k,n+1]-d;
{61} end;
{62} end;
(* Процедура виводу результатів *)
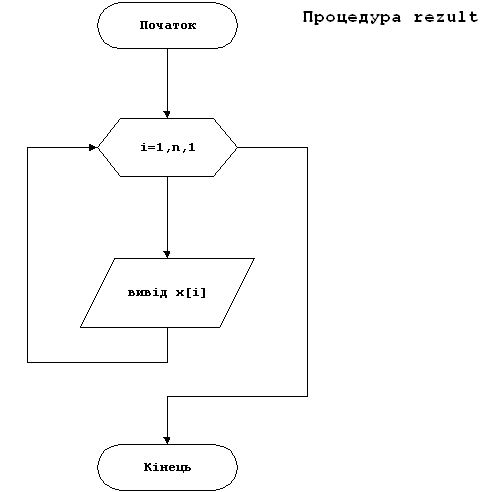
{63} procedure rezult;
{64} begin
{65} writeln('Розв'язки рівняння');
{66} for i:=1 to n do
{67} writeln('x',i,'=',x[i]:8:2);
{68} end;
(* Головна програма *)
{69} begin
{70} clrscr;
{71} vvid(n,a);
{72} for k:=1 to n-1 do begin
{73} mriv(a);
{74} dil(a);
{75} nkoef(a);
{76} end;
{77} nevid(x);
{78} rezult;
{79} end.
![]()
![]()

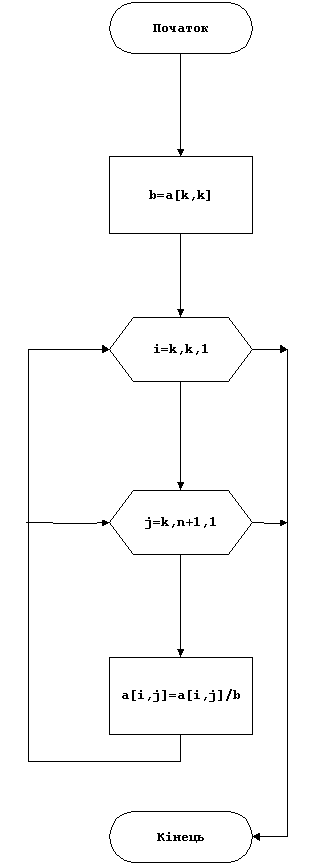
Похожие работы
... . Отже, . 2.3 Опис та інструкція по використанню програми Gauss Дана програма реалізована в інтегрованому середовищі програмування Visual Studio 2008 SP1 мовою програмування С#. Вона дозволяє розв’язувати систему лінійних алгебраїчних рівнянь методом Гауса, записаних в матричній формі, а також методом з пошуком головного елемента, при чому матриці можуть будь-якою вимірністю mxn (m і n – кі ...
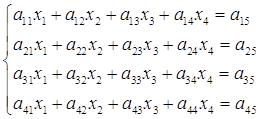
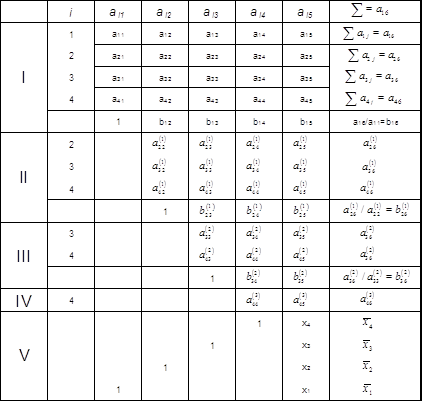
0 комментариев