Навигация
Методы обработки данных гидродинамических исследований при плоскорадиальной фильтрации
1.2 Методы обработки данных гидродинамических исследований при плоскорадиальной фильтрации
Так как газ в скважине движется по нелинейному закону и движение его плоскорадиальное, то мы можем рассмотреть способ определения основных характеристик потока газа с большими скоростями, когда причиной отклонения от закона Дарси становятся значительные инерционные составляющие общего фильтрационного сопротивления.
Для этого рассмотрим фильтрацию по двучленному закону:
Двучленный закон для плоскорадиальной фильтрации имеет вид:
![]() (2)
(2)
где β-дополнительная константа пористой среды определяемая экспериментально.
Выразим скорость фильтрации через массовый расход
![]()
![]()
![]() (3)
(3)
где Qm- массовый расход ![]() , ρ-плотность газа, 2πrh-площадь скважины
, ρ-плотность газа, 2πrh-площадь скважины
и подставим в формулу (2)
![]() (4)
(4)
Разделив переменные и введя функцию Лейбензона(1) получим:
![]() (5)
(5)
Интегрируя уравнение (5) в пределах от r до Rк ,от р до рк найдем соответственно:
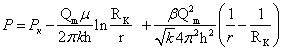 (6)
(6)
Приняв в уравнении (6) ![]() получим:
получим:
![]() (7)
(7)
Переходя от функции Лейбензона к давлению по формуле(8) найдём распределение давления:
![]() (8)
(8)
распределение давления p(r):
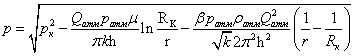 (9)
(9)
где ![]()
запишем уравнение притока газа к скважине:
![]() (10)
(10)
Из формулы(10) видно, что индикаторная линия, построенная в координатах Qатм-(![]() ) для газа, является параболой (рис.4)
) для газа, является параболой (рис.4)
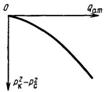
Рис.4 – Индикаторная линия при фильтрации газа по двучленному закону
Подставим теперь в уравнение (10) коэффициенты А и В:
![]() (11)
(11)
получим:
![]() (12)
(12)
Здесь A и B -коэффициенты фильтрационных сопротивлений, постоянные для данной скважины. Они определяются опытным путем по данным исследования скважины при установившихся режимах.
Скважины исследуются на пяти-шести режимах; на каждом режиме измеряется дебит и. определяется забойное давление. Затем скважину закрывают, и давление на забое остановленной скважины принимают за контурное давление pк. Для интерпретации результатов исследований скважин уравнения (12) делением Q на Qaтм соответственно приводят к уравнению прямой:
![]() (13)
(13)
График в координатах Qатм-(![]() )/Qатм представляет собой прямые линии, для которых А- отрезок, отсекаемый на оси ординат, В- тангенс угла наклона прямой к оси абсцисс (рис. 5).
)/Qатм представляет собой прямые линии, для которых А- отрезок, отсекаемый на оси ординат, В- тангенс угла наклона прямой к оси абсцисс (рис. 5).
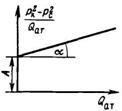
Рис.5 - двучленному закону. График зависимости (![]() )/Qатм от Qатм
)/Qатм от Qатм
Уравнение притока (12) с экспериментально определен ными коэффициентами широко используется в расчетах при проектиро вании разработки месторождений. Кроме того, по значению А, найденному в результате исследования скважины, можно определить коллекторские свойства пласта, например коэффициент гидропроводности:
![]() (14)
(14)
Уравнение притока реального газа к скважине по двучленному закону фильтрации имеет вид
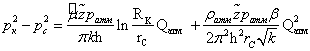 (15)
(15)
где ![]()
![]() ;
; ![]() и являются константами.
и являются константами.
Отметим, что в реальных условиях нельзя считать, что во всем пласте -от стенки скважины до контура питания- справедлив единый нелинейный закон фильтрации.
Похожие работы
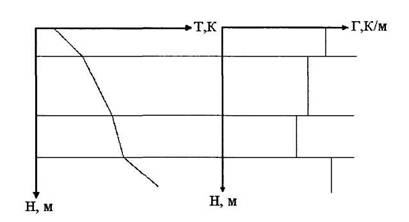
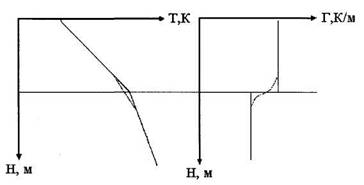
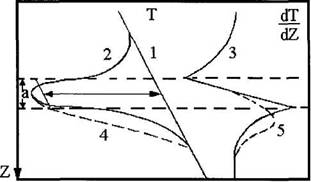
... . Однако полного выравнивания температур никогда не происходит, так как конвективный теплоперенос гораздо мощнее теплообмена. Относительный вклад теплообмена возрастает с уменьшением скорости потока. Квазистационарное распределение температуры в стволе скважины выше продуктивных пластов для потока жидкости описывается следующей приближенной формулой (Чекалюк Э.Б.) T(z) = То- Гг + ГВ (1 - е -т ) ...
0 комментариев