Навигация
Проверка предпосылок и предположений регрессионного анализа
1.2 Проверка предпосылок и предположений регрессионного анализа
Регрессионный анализ является одним из самых распространённых методов обработки результатов наблюдений. Он служит основой для целого ряда разделов математической статистики и методов обработки данных. Регрессионный анализ базируется на ряде предположений и предпосылок, нарушение которых приводит к некорректному его использованию и ошибочной интерпретации результатов.
Если F-критерий и показал, что подгонка модели в целом является удовлетворительной; целесообразно провести анализ остатков для проверки соблюдений предпосылок и предположений.
В этом случае исследуется набор отклонений между экспериментальными и предсказанными значениями зависимой переменной,
![]() .
.
Проверка предпосылок и предположений регрессионного анализа включает в себя следующие задачи:
1) оценка случайности зависимой переменной;
2) оценка стационарности и эргодичности зависимых и независимых переменных;
3) Проверка гипотезы о нормальности распределения ошибок E;
4) Обнаружение выбросов;
5) Проверка постоянства математического ожидания и дисперсии ошибок;
6) Оценка коррелированности остатков;
7) Обнаружение мультиколлинеарности.
1.2.1 Проверка случайности
Построение моделей методом множественного регрессионного анализа требуется выполнение предположения случайности ![]() и
и ![]() в нормальной линейной модели вида
в нормальной линейной модели вида
![]()
где ![]() – вектор наблюдений зависимой переменной;
– вектор наблюдений зависимой переменной;
![]() – матрица наблюдений независимых переменных;
– матрица наблюдений независимых переменных;
![]() – вектор неизвестных коэффициентов;
– вектор неизвестных коэффициентов;
![]() – вектор ошибок.
– вектор ошибок.
Задача проверки случайности может быть разбита на 2 подзадачи:
1) проверка случайности собственной величины Y;
2) проверка случайности выборки, то есть допущения об отсутствии существенного смещения средней величины во времени.
Первая подзадача решается с использованием критерия серий. Для этой цели последовательность наблюдений величины Y представляют последовательностью нулей и единиц, где единицей обозначают значение, превышающее среднее или медиану, и нулем, собственно, значение меньшее медианы. После обозначения вектор наблюдений преобразуется в последовательность серий ![]() где
где ![]() – количество подряд идущих элементов одного вида, i – номер серии.
– количество подряд идущих элементов одного вида, i – номер серии.
Доказано, что при ![]() распределение величины r близится к нормальному с характеристиками
распределение величины r близится к нормальному с характеристиками
![]()
![]()
Тогда с вероятностью 0,954 теоретическое число серий r будет находиться в пределах
![]()
Если фактическое значение ![]() попадает в указанные пределы, то Y можно считать случайной величиной.
попадает в указанные пределы, то Y можно считать случайной величиной.
Серией называется последовательность наблюдаемых значений, перед которыми и после которых расположены наблюдаемые значения другой категории. Если последовательность N наблюдений представляет собой независимые наблюденные значения одной и той же случайной величины, т.е. вероятность знаков (+) и (–) не меняется от одного наблюдения к другому, то выборочное распределение числа серий в последовательности есть случайная величина r со средним значением
![]() (3.1)
(3.1)
и дисперсией
 (3.2)
(3.2)
Здесь ![]() – число наблюдений со знаком (+),
– число наблюдений со знаком (+), ![]() – число наблюдений со знаком (–).
– число наблюдений со знаком (–).
Когда ![]() соотношения (3.1) и (3.2) принимают вид
соотношения (3.1) и (3.2) принимают вид
![]()
Для решения второй подзадачи используется метод последовательных разностей. Элементы исследуемой выборки ![]() располагаются в порядке получения наблюдений и для них вычисляются выборочные среднее и дисперсия
располагаются в порядке получения наблюдений и для них вычисляются выборочные среднее и дисперсия
![]()
Определяют разности ![]() между соседними наблюдениями
между соседними наблюдениями
![]()
и математическое ожидание квадрата разности
![]()
где ![]() – оценка генеральной дисперсии.
– оценка генеральной дисперсии.
Фактическая величина критерия случайности выборки
![]() .
.
Теоретическое значение критерия
![]()
При ![]() для конкретного N гипотеза случайности отвергается.
для конкретного N гипотеза случайности отвергается.
Похожие работы
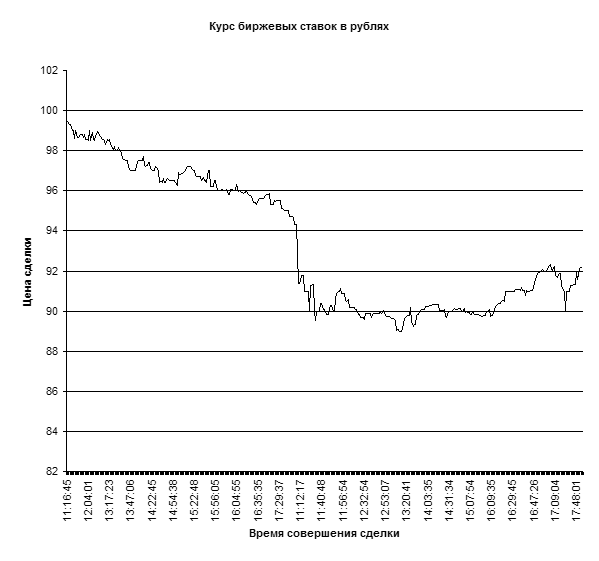
... быстро выполняемой счетной операцией. Данная работа посвящена изучению возможности обработки статистических данных биржевых ставок методами корреляционного и регрессионного анализа с использованием пакета прикладных программ Microsoft Excel. Роль корреляцонно-регрессионного анализа в обработке экономических данных Корреляционный анализ и регрессионный анализ являются смежными разделами ...
... 9472;───────┴─────────┘ Реализация алгоритма многомерного регрессионного анализа начинается с расчета важнейших статистических характеристик исходной информации и матрицы выборочных парных коэффициентов корреляции. Рассмотрим более подробно вариационные характеристики переменной у: ...
... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...
... на зависимую и определение расчётных значений зависимой переменной (функции регрессии). Решение всех названных задач приводит к необходимости комплексного использования этих методов. Корреляционный и регрессионный анализ. Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле ...
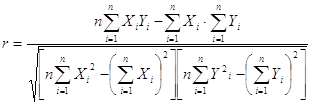
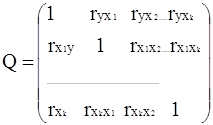
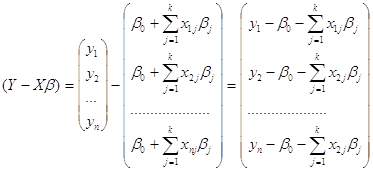
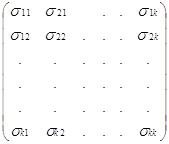

0 комментариев