Навигация
Решение задач линейного программирования симплекс-методом
1.2 Решение задач линейного программирования симплекс-методом
Задача ЛП в общем виде может быть записана так:
(c, x) − max
Ax = b,
где c =(c1,c2,...,cn)T – мерный вектор-столбец коэффициентов; x =(x1,x2,...,xn)T – мерный вектор-столбец неизвестных; A =(aij),m × n – матрица коэффициентов; B =(b1,b2,...,bm) – вектор-столбец коэффициентов.
В этом случае мы имеем дело с неотрицательными решениями системы уравнений.
Любая задача линейного программирования с помощью элементарных преобразований может быть приведена к каноническому виду.
F(x)=c1x1+c2x2+...+cnxn ->max(min)
![]() a11x1+a12x2+...+a1nxn +х n +1 = b1
a11x1+a12x2+...+a1nxn +х n +1 = b1
a21x1+a22x2+...+a2nxn+х n +2 = b2 (3)
.......................
am1x1+am2x2+...+amnxn+х n +т = bm
xi≥0 (i=1..n),
где F(x) – целевая функция; х1,х2,…,хn– базисные переменные; остальные переменные называются свободными.
Задача имеет m+n ограничений, среди них m ограничений типа равенства и n ограничений неотрицательности. По определению крайняя точка удовлетворяет n линейно-независимым ограничениям задачи как точным равенствам.
Таблица 1 – Система ограничений и целевая функция
| Базисные переменные | Свободные члены | X 1 | X 2 | … | X n | X n+1 | X n+2 | … | Xn+m |
| X n+1 | b1 | a 11 | a 12 | … | a 1n | 1 | 0 | … | 0 |
| X n+2 | b2 | a 21 | a 22 | … | a 2n | 0 | 1 | … | 0 |
| … | … | … | … | … | … | … | … | … | … |
| X n+m | b m | a m1 | a m2 | … | a mn | 0 | 0 | … | 1 |
| F(x) | 0 | -c1 | -c2 | … | -cn | 0 | 0 | … | 0 |
Рассмотрим алгоритм перехода к следующим симплекс-таблицам:
1. Выбираем ключевой столбец. Это столбец соответствующий минимально отрицательному (максимально положительному) элементу последней (индексной) строке:
Если отрицательных элементов в индексной строке нет, то план оптимальный.
2. В ключевом столбце выбираются положительные коэффициенты, если таких нет, то задача не имеет решений;
3. Выбираем ключевую строку:
Среди выбранных коэффициентов столбца, для которых абсолютная величина отношения соответствующего свободного члена к этому элементу минимальна.
Ключевой элемент – это элемент, стоящий на пересечении ключевого столбца и ключевой строки;
4. Базисная переменная из ключевой строки переводится в разряд свободных, а свободная переменная в ключевом столбце переводится в разряд базисных. Строится новая таблица;
5. В новой таблице:
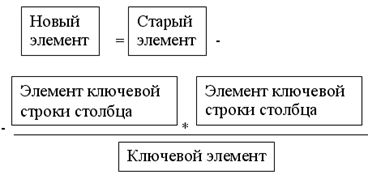
5.1 Все элементы ключевой строки делятся на ключевой элемент.
5.2 Все элементы ключевого столба равны нулю, за исключением ключевого элемента.
5.3 Столбец, у которого в ключевой строке имеется ноль, в новой таблице будет таким же.
5.4 Строка, у которой в ключевом столбце имеется ноль, в новой таблице будет такой же.
5.5 В остальные клетки записывается результат преобразования элементов старой таблицы.
6. Переход к шагу 1.
Через конечное число итераций либо будет получено решение задачи линейного программирования, либо будет установлено, что решение неограниченно.
2. Постановка задачи
Для изготовления изделий двух видов склад может отпустить металла не более 150 кг, причем на изделие первого вида расходуется пять килограмм, а на изделие второго вида три килограмма. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если изделий первого вида требуется изготовить не более 20 штук, а изделий второго вида не более 25 штук, причем одно изделие первого вида стоит 7 руб., а изделие второго вида стоит 8 руб.
Похожие работы
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... - формула (1.2), ограничений не отрицательности переменных (есть, нет) - формула (1.3) (1.1) i = 1,… m (1.2) (1.3) Алгоритм решения задач линейного программирования требует приведения их постановки в канонический вид, когда целевая функция ...
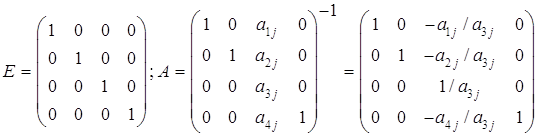
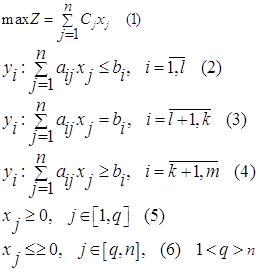
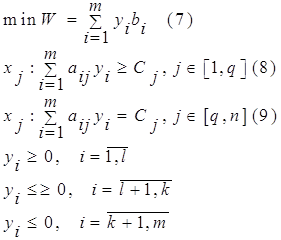
0 комментариев