Восприятие и интерпретация некоторого сообщения инженером по знаниям. В результате в памяти инженера образуется некоторая модель предметной области

3.  Восприятие и интерпретация некоторого сообщения инженером по знаниям. В результате в памяти инженера образуется некоторая модель предметной области.

4.  Кодирование и вербализация модели в форме некоторого поля знаний, спроектированного инженером по знаниям для реализации в базе знаний.

Это трудная задача – добиться максимального соответствия между действительным состоянием предметной области и некоторым полем знаний. Поле знаний может быть представлено как пирамида, где следующий уровень служит для восхождения на новую ступень обобщения и углубления знаний.

В искусственном интеллекте используется термин – формирование знаний, который обозначает процесс анализа данных и выявления скрытых закономерностей с использованием специального математического аппарата и программных средств ЭВМ. Основные методы извлечения знаний представлены на рис.

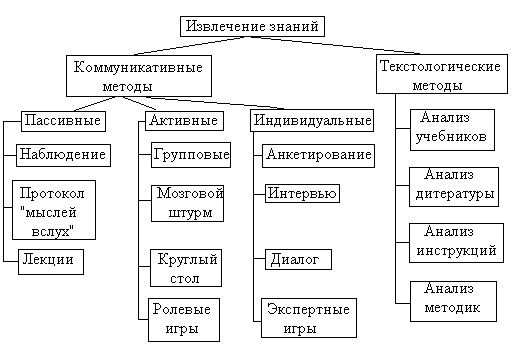
Все эти методы позволяют сформировать поле знаний на основании следующего алгоритма:

1.Определение входных и выходных данных, структура которых существенно влияет на форму и содержание поля знаний.

2.Составление словаря терминов и наборов ключевых фраз, при этом особенно важен словарь терминов.

3.Выявление объектов и понятий, выбор значимых понятий и их признаков.

4.Выявление связей между понятиями, построение сети ситуаций, где связи только намечены, но пока не поименованы.

5.Структуризация понятий с выявлением понятий более высокого уровня обобщенгия и детализацией на более низком уровне.

6.Построение пирамиды знаний с иерархической лестницей понятий по уровню общности.

7.Определение временных, причинно-следственных и других отношений с их обозначением путем присвоения имен свеем связям.

8.Определение стратегий принятия решений. Выявление цепочек рассуждений связывает все сформированные ранее понятия и отношения в динамическую систему поля знаний.

Модели представления знаний

От формы представления знаний зависит характеристика и свойства систем искусственного интеллекта. В отличие от знаний, используемых человеком, в компьютере используется моделирование знаний. Под моделью знаний понимается способ описания знаний в базе знаний.

В общем случае модели представления знаний могут быть условно разделены на декларативные и процедурные. Декларативная модель основывается на предположении, что проблема представления некоторой предметной области решается независимо от того, как эти знания будут использоваться. Поэтому модель состоит как бы из двух частей: структур, описывающих знания и механизма вывода, оперирующего этими структурами, независимо от содержательного наполнения структур. При этом синтаксические и семантические аспекты разделены. Описания выполняемых процедур не содержатся в явном виде. Предметная область представляется в виде описания ее состояния, а вывод решения основывается в основном на процедурах поиска в пространстве состояний.

Процедурная модель основывается не небольших программах (процедурах), которые определяют, как поступать в конкретных ситуациях. В этой модели семантика заложена непосредственно в описании элементов базы знаний. Общие правила представлены в виде специальных целенаправленных процедур.

Требования к моделям представления знаний:

- однородность представления;

- простота понимания;

- упрощение механизма управления выводом.

Наиболее распространенными являются четыре модели представления знаний в интеллектуальных системах и их комбинации:

- логическая или логика предикатов;

- продукционная;

- семантические сети;

- фреймовая модель.

Представление знаний с помощью логики предикатов

Логика предикатов используется как один из языков представления знаний. В любом языке для создания языковых форм должно быть определено следующее:

- множество знаков, которое можно в нем использовать;

- полное определение слов через знаковые последовательности;

- грамматические правила образования предложений из слов (синтаксические правила).

Каждое слово из предложения соответствует объектам и действиям того реального мира, который описывается этим языком. Таким образом в языке присутствуют слова, которые описывают сущности, и слова, которые описывают атрибуты сущностей и действия над ними.

Для формулировки знаний о некоторой предметной области средствами логики предикатов в проблемной области выделяют два основных типа понятий:

- дискретные объекты, которые называют сущностями;

- отношения между сущностями.

Именам отношений соответствует термин «предикат», а сущностям – аргументы. Символы, используемые для обозначения высказываний, называют атомами. Таблицей истинности формулы называется таблица, содержащая истинностные значения формулы при всех возможных комбинациях истинностных значений входящих в нее атомов..

Логика предикатов (исчислений) основана на логике (исчислении) высказываний. Высказыванием (суждением) называют предложение, принимающее только два значения – «истина» или «ложь». Логический вывод (силлогизм) в классической логике строится двумя путями: дедукцией и индукцией. В современной логике вывод строится также абдукцией. Индукция и абдукция называются вероятностными силлогизмами.

Дедукция – вывод, позволяющий получать заключение из большой или малой посылки. Большая посылка называется дедуктивным правилом, малая – фактическим заявлением (декларацией).

Пример: Большая посылка: рыба – живое существо, умеющее плавать.

Малая посылка: карась – рыба.

Вывод: карась – живое существо, умеющее плавать.

Большая и малая посылка называются данными о знаниях или просто знаниями и их объем должен быть достаточно большим.. Упорядоченное множество таких знаний составляет базу знаний..

Дедуктивное правило позволяет детализировать и формализовать причинно-следственные связи явлений (процессов) и дел (предметов), т.е. это знания, необходимые для выполнения алгоритма принятия решений. Основная часть знаний кодируется не только арифметическими, но и логическими символами. Таким образом требуется специальный язык для ЭВМ.

Индукция – получение большой посылки из заключения ее малой посылки. Можно ли считать правомерным определение «рыба – это живое существо, умеющее плавать»» в качестве большой посылки, исходя из того, что известны многие виды рыб? Вывод неправомерен, т.к. могут быть неизвестные виды рыб, перемещающиеся по суше. По мере накопления наблюдений повышается достоверность большой посылки.

Абдукция – получение малой посылки из заключения и большой посылки. На основании факта, что некоторые из живых существ умеют плавать, делается заключение, что это живое существо – рыба. Однако этот вывод нельзя считать безусловно достоверным. Человек в обыденной жизни имеет постоянно дело с нечеткими, вероятностными оценками.

Пример силлогизма:

- Все металлы электропроводны;

- медь – металл;

Заключение: медь электропроводна.

Предикатом или логической функцией называется функция от любого числа аргументов, принимающая истинностные значения «истина» или «ложь». Аргументы принимают значения из произвольного конечного или бесконечного множества М, называемого предметной областью. Предикат от n аргументов является n-местным предикатом.

Все операции исчисления высказываний переносятся в исчисления предикатов и используются для связывания предикатов и формул, т.е. позволяют получить из простых высказываний сложные. Основные операции алгебры логики:

Отрицание. Высказывание истинно, если высказывание А ложно. А ложно, если А истинно.

Конъюнкция. А ^ В (А*В) – логическое умножение. Высказывание истинно только в тех случаях, когда истинны А и В.

Дизъюнкция. А В – логическое сложение А+В. Высказывание истинно только в случае, если истинно хотя бы одно из слагаемых.

А В (А В) Импликация или следование В из А. Читается также «если А, то В». Высказывание ложно только в том случае, если А истинно и В ложно.

А В – эквивалентность. «А тогда и только тогда, когда В». Высказывание истинно тогда и только тогда, когда А и В имеют одно и то же истинное значение.

В логике предикатов используются основные свойства логических операций: свойства ассоциативности, коммутативности, дистрибутивности, законы идемпотентности и де Моргана.

В логике предикатов для компактной записи высказываний типа « для любого x истинно F(x)» и «существует такое x, для которого истинно F(x)», дополнительно вводятся две операции – квантор общности  и квантор существования . Вышеприведенные высказывания можно записать в следующем виде:

xF(x) – высказывание истинно, когда F(x) истинно для всех x  M и ложно в противоположном случае.

xF(x) – высказывание истинно, когда существует элемент x  M, для которого F(x) истинно и ложно в противоположном случае.

В логике предикатов обычно используются шесть типов символов:

А) Предикатные переменные x, y, z, u, v, w или те же буквы с индексами.

Б) Предметные константы a, b, c, d, e или те же буквы с индексами.

В) Функциональные символы – f, g, h или те же буквы с индексами.

С) Предикатные символы p, q, r, s, t или те же буквы с индексами.

Д) Логические символы

Е) Вспомогательные символы – круглые скобки, запятые и т.п.

Вывод, дающий заключение из двух посылок можно представить следующим образом:

Предпосылка 1. Все металлы электропроводны.

Предпосылка 2. Медь металл.

Заключение: медь электропроводна.

Если вместо имен субъектов поставить переменные x, y, z, то можно получить логическую формулу:

Предпосылка 1. металл (x) электропроводен (x)

Предпосылка 2. металл (медь)

Заключение: электропроводна (медь).

Логика предикатов рассматривает вопрос, можно ли, представляя предложения в виде логических формул, с помощью выводов получить из нескольких логических формул некоторую конечную логическую формулу.

Таким образом в логике предикатов основным объектом исследования является формула. При ее определении используется понятие «терм» (некоторая сущность), объединяющая название элементарных функций, к которым применима предикатная буква. Терм определяется следующим образом:

- всякая предметная переменная или предметная константа являются термами;

- если f – n-местная функция из n аргументов и t₁ …..t_n – термы, то f(t₁…..t_n) есть терм;

Выражение p (t₁…..t_n), где p – предикатный символ m аргументов и t₁…..t_m – термы называется атомарной функцией или атомом.

Атомы и всякие выражения из них есть правильно построенные формулы (ППФ).

Пример;

Предпосылка 1. (логическая формула) x (p(x)) q(x)

Предпосылка 2. (атом) p(a)

Заключение (атом) q(a)

Здесь p – металл, q – электропроводность, a – медь.

Интерпретация. Формула имеет определенный смысл, т.е. обозначает определенное высказывание, если существует какая-либо интерпретация.. Интерпретировать формулу – значит связать с ней определенное множество М, т.е. конкретизировать предметную область, называемую областью интерпретации и указать соответствие, относящееся:

- каждой предметной константе в формуле конкретный элемент из М;

- каждой n-местной функциональной букве в формуле – конкретную n-местную функцию на М;

- каждой n-местной предикатной букве в формуле конкретное отношение между n элементами из М.

Иными словами – интерпретирование формул исчисления предикатов это конкретизация предметной области М и соответствия между символами, входящими в формулы с одной стороны, и элементами, функциями и отношениями на М с другой.

Пример: элементарная формула G(f(a,b), g(f,b))

Интерпретация: М – множество действительных чисел; a,b –числа 2 и 3 соответственно; f – функция сложения (f(a,b) = a+b); g – функция умножения (g(a,ba0 =ab); G - отношение «не меньше» . Формула обозначает высказывание « сумма 2+3 не меньше произведения 2*3». Результат «ложь». Если изменить интерпретацию, b = 1 или b = 2, то результатом будет «истина».

Другая формула при той же интерпретации:

G(f(g(x,x),g(y,y),g(a,g(x,y)))

Формула обозначает высказывание

x² + y²> 2xy

Высказывание верно при любом x и y из М и всегда истинно.

Для описания высказываний на языке предикатов в заданной предметной области часто для обозначения предикатных букв и констант используются слова или сокращения, которые являются названиями определяемых ими свойств, отношений, объектов.

( x) [ Дельфин (x) умный (x)]

Дельфин наделен умственными способностями

( x) [Слон (x) --- цвет (x, серый)]

Все слоны имеют серую окраску.

Логика предикатов применяется для решения сравнительно простых задач.

Продукционные модели знаний

Продукционные модели занимают особое положение, т.к. они являются наиболее декларативным способом представления знаний. Продукционная модель представления знаний – это набор правил вида

ЕСЛИ «условие, ТО «действие»,

где «условие» образец для поиска в базе данных (утверждение о состоянии базы данных); «действие» - действие, выполняемое при успешном исходе поиска в базе (процедуры, которые могут изменять состояние базы данных). Действия могут быть промежуточными, выступающие далее как условия и целевыми, завершающими работу системы.

В продукционных моделях используются некоторые элементы логических моделей, что позволяет организовать из них эффективные процедуры вывода, а с другой стороны, более наглядно отражают знания, чем классические логические модели. Правила вывода в этих моделях называются продукциями.

Системы продукций – это набор правил, используемый как база знаний, поэтому его еще называют базой правил. Продукции соответствуют навыкам в долгосрочной памяти человека. Подобно навыкам в долгосрочной памяти эти продукции не изменяются при работе системы. Они вызываются «по образцу» для решения данной проблемы.. Рабочая память продукционной системы соответствует краткосрочной памяти или текущей области внимания человека. Содержание рабочей области после решения задачи не сохраняется.

Примеры фактов и правил.

Факт 1. Зажженная плита – горячая.

Правило 1. Если положить руку на зажженную плиту, то можно обжечься.

В общем виде под продукцией понимается выражение следующего вида:

( I ); Q; P; A B; N

Здесь I – имя продукции, с помощью которого эта продукция выделяется из всего множества продукций. В качестве имени может выступать какое-то словосочетание или порядковый номер продукции. Q - характеризует сферу применения продукции. Примерами сфер применения могут быть «роботизированный участок», «приготовление пищи» и другие. Разделение знаний на отдельные сферы позволяет экономить время на поиск нужных знаний.

Основным элементом продукции является ее ядро А В. Интерпретация ядра продукции может быть различной, но чаще всего звучит так: ЕСЛИ А, ТО В1, ИНАЧЕ В2. Элемент Р – условие применимости. Обычно Р представляет собой логическое выражение. Когда Р принимает значение «истина» ядро активизируется. Если Р «ложно», то ядро не может быть использовано. Элемент N описывает постусловия продукции. Это действия, которые выполняются только в том случае, если ядро продукции реализовалось.

В системе продукций должны быть заданы специальные процедуры управления продукциями, с помощью которых происходит активизация продукций и выбор для выполнения той или иной продукции из числа активизированных. Продукционные системы имеют давнюю историю. Их ограничение – в применении к крупномасштабным задачам, т.к. большое число правил приводит к замедлению скорости вывода. Кроме того, продукционная модель не имеет механизма вывода из тупиковых состояний в процессе поиска. Она продолжает работать, пока не будут исчерпаны все допустимые продукции.

Преимущества продукционной модели представления знаний:

- простота и гибкость выделения знаний;

- отделение знаний от программы поиска;

- модульность продукционных правил (правила не могут вызывать другие правила);

- простота пополнения и модификации;

- возможность эвристического управления поиском;

- возможность трассировки «цепочки рассуждений»;

- простота механизма вывода;

- независимость от выбора языка программирования;

- для ПК это простой и точный механизм использования знаний с высокой однородностью, описанных по одному синтаксису;

- продукционные правила являются правдоподобной моделью решения задачи человеком.

Фрагмент управления транспортным роботом:

Правило 1: Если i-й накопитель пуст – перейти к i+1 накопителю.

Правило 2: Если в i-том накопителе есть детали И тележка робота не заполнена, то освободить накопитель и перейти к i+1 накопителю.

Правило 3: Если тележка робота заполнена, то отвезти детали на склад и вернуться к i-тому накопителю.

Продукционная система имеет три компонента. Это знания, представленные в виде системы продукций в базе правил (БП), образцы условий в рабочей памяти (РП) и механизм вывода (МВ) (рис. ).

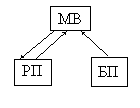
Машина (механизм) вывода.

Программа, управляющая перебором правил называется машиной вывода (интерпретатором правил). МВ выполняет две функции: а) просмотр существующих фактов из рабочей памяти (базы данных) и правил из базы знаний с добавлением (по мере возможности) в рабочую память новых фактов; б) определение порядка просмотра и применения правил.

Этот механизм управляет процессом консультации, сохраняя для пользователя информацию о полученных заключениях, и запрашивает у него информацию, когда для срабатывания очередного правила в РП оказывается недостаточно данных.

МВ представляет собой небольшую по объему программу и включает два компонента – один реализует вывод, второй управляет этим процессом.

Действие компонента вывода основано на применении правила, называемого modus ponens. «Если известно, что истинно утверждение А и существует правило ЕСЛИ А ,ТО В, тогда утверждение В также истинно». Правила срабатывают, когда находятся факты, удовлетворяющие их левой части. «Если истинна посылка, то должно быть истинно и заключение». Компонент вывода должен функционировать даже при недостатке информации.

Управляющий компонент определяет порядок применения правил и выполняет четыре функции:

1. Сопоставление = образец правила сопоставляется с известным фактом.

2. Выбор – если в конкретной ситуации может быть применено сразу несколько правил, то из них выбирается одно, наиболее подходящее по заданному критерию (разрешение конфликтов).

3. Срабатывание – если образец правила при сопоставлении совпал с каким-либо фактом из РП, то правило срабатывает.

4. Действие – РП подвергается изменению путем добавления в нее заключения сработавшего правила. Если в правой части правила содержится указание на какое-либо действие, то оно выполняется.

Интерпретатор (МВ) работает циклически. В каждом цикле он просматривает все правила, чтобы выявить те, которые совпадают с известными на данный момент фактами из РП. После выбора правило срабатывает, его заключение заносится в РП, и цикл повторяется снова. В одном цикле может сработать только одно правило.

Если несколько правил успешно сопоставлены с фактами, то МВ производит выбор по определенному критерию единственного правила, которое срабатывает в данном цикле.

Цикл работы МВ показан на рис.

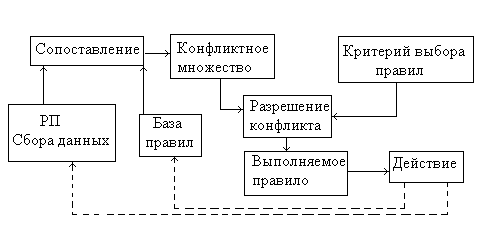
Работа МВ зависит только от состояния РП и от состава базы знаний. На практике обычно учитывается история работы, т.е поведение МВ запоминается в памяти состояний, которая содержит протокол системы. (рис. ).

Пример:

П1. Если (отдых летом) И (человек активный)

ТО (ехать в горы)

П2. Если (любит солнце) ТО (отдых летом)

Предположим, что в систему поступили факты: человек активный и любит солнце.

1-проход.

Шаг 1. Пробуем П!, не работает (не хватает данных – отдых летом)

Шаг 2. Пробуем П2, работает, б базу поступает факт – отдых летом.

2-й проход.

Шаг 3. Пробуем П1, работает. Активизируется цель (ехать в горы), которая выступает как совет.

Стратегия управления выводом.

От метода поиска зависит порядок применения и срабатывания правил. Процедура выбора сводится к определению направления поиска и способа его осуществления.

Прямой и обратный вывод. В системах с прямым выводом по известным фактам отыскивается заключение, которое следует из этих фактов. Если такое заключение найдено, то оно заносится в РП. Такой вывод называют выводом, управляемым данными.

При обратном выводе вначале выдвигается гипотеза, а затем МВ как бы возвращается назад, переходя к фактам, пытаясь найти те, которые подтверждают гипотезу. Если она правильна, то выдвигается следующая гипотеза, детализирующая первую и являющуюся по отношению к ней подцелью. Далее отыскиваются факты, подтверждающие истинность подчиненной гипотезы. Вывод такого типа называется управляемым целями. Применяется в тех случаях, когда цели известны и их сравнительно немного.

В системах с более сотен правил желательно использовать стратегию управления выводом, позволяющую минимизировать время поиска решения и тем самым повысить эффективность работы системы. К числу таких стратегий относятся поиск в глубину, поиск в ширину, разбиение на подзадачи и альфа-бета стратегия.

При поиске в глубину в качестве подцели выбирается та, которая соответствует следующему, более детальному уровню описания задачи.

При поиске в ширину анализируются все начальные варианты. Разбиение на подзадачи заключается в выделении подзадач, решение которых рассматривается как достижение промежуточных целей. Альфа-бета стратегия заключается в удалении ветвей, неперспективных для успешного поиска.

Работа продукционной системы инициируется начальным описанием (состоянием) задачи. Из продукционного множества правил выбираются правила, пригодные для применения на очередном шаге. Эти правила могут создавать так называемое конфликтное множество. Для выбора правил из конфликтного множества существуют стратегии разрешения конфликтов, которые могут быть достаточно простыми, например, выбор первого правила. Могут быть и сложными эвристическими правилами. Следует отметить, что конфликтные множества представляют собой простейшие базы целей.

Кроме базовой структуры продукционных систем необходимы дополнительные средства – управление данными, уточняющими смысл:

Триплет: объект – атрибут (необходимый признак) – значение;

Пример; робот – степень подвижности – 4.

Четверка: – атрибут (необходимый признак) – значение – степень достоверности.

Пример: сверло – материал Р!* - стойкость 25 мин. – достоверность 0,7.

Условная часть может состоять из одного или нескольких условий, соединенных связкой И. Заключительная часть показывает данные, которыми следует пополнить РП при выполнении условной части. На практике при необходимости расширяют эти правила. Например, используют связку ИЛИ. В условной части, вводят условную часть с вычислениями на основании содержимого РП, либо вводят заключительную часть с пометкой – не дополнять содержимое РП.

Визуально такое отношение можно представить в виде графа с древовидной структурой (рис. ).

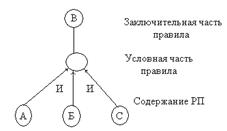
Если существует множество правил, из которых выводится одно и то же заключение, то выполняется процедура ИЛИ над всеми заключениями из этих правил. Таким образом всю систему продукций можно представить в виде одного графа И/ИЛИ (рис. ).

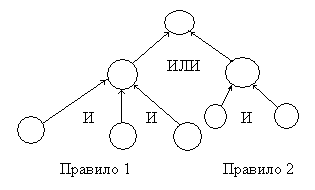
Система, реализующая прямую цепочку рассуждений, на основании имеющихся условий делает возможным логические выводы. Система, реализующая обратную цепочку рассуждений по имеющимся выводам, ищет необходимые для них условия.

По такому графу обратный вывод – это поиск пути на графе. Управление последовательностью поиска осуществляется механизмом вывода. Могут быть использованы различные стратегии поиска. Используются также системы с двунаправленными выводами, где сначала оценивается небольшой объем полученных данных и выбирается гипотеза (прямой вывод), а затем запрашиваются данные для принятия решения о пригодности данной гипотезы.

Для повышения эффективности функционирования ИС в проблемной области с увеличением числа правил используются методы группирования, упорядочения информации в РП, предварительной компиляции правил в виде графа.

Пример работы продукционной системы. Рассматривается роботизированный участок.

Правило 1: ЕСЛИ (станок без заготовки) (1)

И (заготовка на накопителе) (2)

ТО (робот подает заготовку на станок) (3)

Правило 2: ЕСЛИ (накопитель подал заготовку в загрузочную позицию) (4)

ТО (заготовка в загрузочной позиции)

Действия:

1.  Допустим, в РП вносятся 1 и 4 образцы и рассматривается возможность применения правил. Сначала МВ сопоставляет образцы из условной части правил с образцами в РП.

2.  Если все образцы имеются в РП, то условная часть считается истинной, в противном случае – ложной. Т.к. в условной части (2) отсутствует, то условная часть правила 1 считается ложной. Но правило 2 выполняется, т.к. посылка (4) верна, поэтому МВ выполняет его заключительную часть, и образец (2) заносится в РП.

3. Вторично применяется правило 1, т.к. правило 2 уже было применено и выбыло из числа кандидатов. Т.к. (1) истина и (2) истина, то (3) – вывод. В итоге правил, которые можно было бы применить не остается и система останавливается.

4. Для описания задач часто используют дерево решений.

Семантические сети

В бытовом понимании семантика означает смысл слова, действия, художественного произведения и т.п. Семантическая сеть – это граф, вершинам которого сопоставляются понятия (объекты, процессы, явления), дуги графа – это отношения между вершинами.

Возможные отношения в семантических сетях (не полный список):

Агент – это то, что (тот, кто) вызывает действие. Агент часто является подлежащим в предложении. Например, «Иванов ударил мяч».

Объект – это то, на что (на кого) направлено действие. В предложении объект часто выполняет роль прямого дополнения. Например, «Робот взял пирамиду».

Инструмент – это средство, которое используется агентом для выполнения действия. Например, «Иванов открыл дверь с помощью ключа».

Соагент – служит как подчиненный партнер главному агенту. Например, «Иванов сдал экзамен с помощью Петрова».

Пункт отправления и пункт назначения – это отправная и конечная позиция при перемещении агента или объекта. Например, «Робот переместился от одного станка к другому».

Траектория – это перемещение от пункта отправления к пункту назначения. Например, «Они прошли через дверь по ступенькам на лестницу».

Средство доставки – то в чем или на чем происходит перемещение. Например, «Иванов всегда едет домой на машине».

Местоположение – то место, где произошло (происходит, будет происходить) действие. Например, «Он работал за столом».

Потребитель – то лицо, для которого выполняется действие. Например, «Иванов собрал шпаргалки для Кати».

Сырье – это, как правило, материал из которого что-то сделано или состоит. Обычно сырье вводится предлогом из. Например, «Иванов собрал робот из интегральных схем».

Время – указывает на момент совершения действия. Например, «Он закончил работу поздно вечером».

Пример семантической сети: Поставщик осуществил поставку изделий по заказу клиента до 1 июня 2008 г. в количестве 1000 шт.

Поиск в семантической сети: Какой объект находится на желтом блоке?

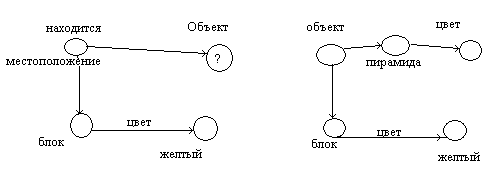
Совместив запрос с сетью получим ответ – пирамида.

Классификация сетей.

По структуре:

Сети простого типа – у которых вершины не имеют собственной внутренней структуры.

Однородные сети – при одинаковых отношениях между вершинами.

Сети иерархического типа – таким сетям свойственны структуры с вершинами разного ранга, имеющими разный уровень или подчиненность от низших к высшим.

По характеру отношений, приписываемых дугам сети:

Функциональные сети. Дуги отражают тот факт, что вершина, из которой выходит дуга, играет по отношению к вершине, куда идет дуга, роль аргумента. Описания, соответствующие вершине – функции, задают процедуру нахождения результата.

Сценарии – однородные сети, в которых в качестве единственного отношения выступает отношение нестрогого порядка (например, отношение «не раньше, чем»), которое допускает одновременность. Чаще всего эти отношения определяют все возможные последовательности событий.

Семантические сети – в отличие от двух первых – неоднородны и иерархичны.

Семантические сети делятся на интенсиональные и экстенсиональные. Интенсиональная сеть содержит интенсиональные знания и описывает общую структуру модернизируемой предметной области на основе абстрактных объектов и отношений, т.е. обобщенных представителей некоторых классов объектов и отношений. Например, такие объекты как Производственный участок, груз, деталь могут являться обобщенными понятиями множества значений от которых образуется множество имен конкретных производственных участков (токарный, прессовый и т.п.), множество имен грузов (заготовка, кассета), множество классов деталей (болт, вал, гайка и т.п.).

Экстенсиональная семантическая сеть описывает экстенсиональные знания о модернизируемых объектах, являясь как бы «фотографией» его текущего состояния.

Интенсиональная сеть предложения «Робот сверлит отверстие в детали сверлом диаметром 10 мм.

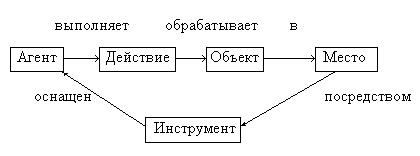
Рис. Интенсиональная сеть.

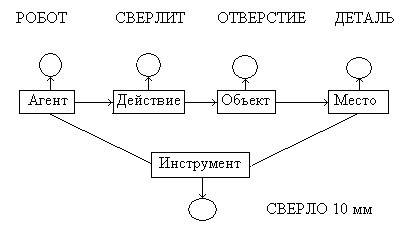
Рис. Экстенсиональная сеть.

В семантических сетях используются три основных типа объектов: понятия, события, свойства.

Понятие – это сведения об абстрактных или физических объектах предметной области. Общие понятия интерпретируются как множество параметров или констант.

События – это действия, которые могут внести изменения в предметную область .Результатом события является некоторое новое состояние предметной области. Можно задать желаемое (целевое) состояние предметной области и поставить задачу отыскания в семантической сети последовательности событий, приводящей к новому состоянию.

Свойства – используются для уточнения понятий или событий. Для понятий это особенности или характеристики (цвет, размеры, качество). Для свойств - продолжительность, время, место.

Семантические отношения делят на четыре класса: лингвинистические, логические, теоретико-множественные и квантифицированные.

Лингвинистические – наиболее употребительные – падежные, к которым относятся агент и т.п. Другой тип – это характеризация глаголов и атрибутивных отношений. К характеризации глаголов относятся наклонение, время, род, число, залог. Атрибутивные отношения – цвет, форма, размер. Например: «Большие красные шары».

Логические отношения представляют собой операции алгебры логики..

Теоретико-множественные – это подмножество, супермножество, элемент множества, отношение части и целого и др. Этот класс отношений используется для построения иерархических соподчиненных структур, для представления обобщенной информации.

Квантифицированные отношения – это логические кванторы общности и существования.. Логические кванторы применяются для представления знаний декларативного типа. Например: «каждый станок требует профилактического ремонта», «Существует робот А, который может обслуживать станки группы В».

Важным понятием в семантических сетях является десигнат – уникальное внутрисистемное имя, которое ставится в соответствие некоторому объекту в предметной области, если о нем в данный момент времени нет полной информации. Например, «Станок С1 имеет накопитель». Это предложение имеет неопределенность относительно характеристик накопителя. По мере поступления информации будут уточняться емкость накопителя и другие данные.

(F1: имеет агент Станок объект D1)

(D1: имя накопитель)

(D1: габарит ______)

(D1: емкость _______)

F1 – метка факта, D1 – метка десигната.

В момент первого напоминания вводится информация, которая используется в дальнейшем. В семантических сетях информация может представляться в фреймовом виде..

При построении интеллектуальных банков данных на основе семантических сетей основным принципом их организации является разделение экстенсиональных и интенсиональных знаний, при этом экстенсиональные семантические сети являются основой базы данных, а интенсиональные сети – основой базы знаний.

Особенности представления знаний в семантических сетях состоят в следующем:

- в семантической сети могут быть представлены такие виды объектов как понятия, события, специализированные методы решения. Увеличение номенклатуры объектов снижает однородность сети и приводит к необходимости увеличения набора механизмов и методов вывода.

- многомерность семантических сетей позволяет представить в них сложные семантические отношения, связывающие отдельные понятия, понятия и события в предложении, а также предложения в текстах.

- на каждой стадии формирования решения можно четко разделить полное знание системы (полная семантическая сеть) и текущее знание – возбуждаемый участок сети, в котором производятся некоторые операции (процесс вывода, понимания и т.п.).

Известны многие варианты семантических сетей, общие характеристики которых сводятся к следующему:

- описание объектов предметной области происходит на уровне естественного языка;

- все знания, включая вновь поступающие факты, а также специализированные методы решения, накапливаются в относительно однородной структуре памяти;

- определяется ряд более или менее унифицированных семантических отношений между объектами, которым ставятся в соответствие унифицированные методы вывода;

- запросы вместе с методами вывода определяют участки знания (семантической сети), имеющие отношение к поставленной задаче, фиксируя тем самым понимание запроса и вытекающую из него цепь выводов, соответствующих решению задачи; выводы в семантических сетях отличаются значительной полнотой.

Управление выводом.

Механизм вывода использует метод генерации выводов, так называемый «метод распространяющейся активности и техники пересечений». Процесс осуществляется построением на основе введенных высказываний цепочек возможных выводов во всех направлениях до тех пор, пока в сети не обнаружится пересечение или не найден фрагмент, отражающий поставленный запрос к базе знаний. Недостаток – сложность организации процедуры вывода. Область применения семантических сетей – системы обработки естественного языка, системы технического зрения и другие.

Фреймовое представление знаний

Все типы моделей знаний перед их применением в конкретной системе необходимо заполнить информацией, уточняющей используемые общие символы и понятия. Модель без наполнения информацией до уровня соответствия единичной реальной системе называется абстрактной.

В обычном диалоге значительная часть информации не выражается собеседником определенно и ясно (умалчивается). Предполагается, что оба собеседника хорошо знают тему разговора и нет смысла лишний раз описывать очевидные детали, которые являются стандартными для данной ситуации.

Термин фрейм (frame – рамка, остов) предложен в 1975 г. Марвеллом Минским. Фрейм – это единица представления знаний, заполненная в прошлом, детали которой могут быть изменены согласно текущей ситуации, т.е. это минимальное описание, которое еще сохраняет сущность описываемого явления и такое, что дальнейшее ее сокращение приводит к потере сущности. Получается, что фрейм – это абстрактный образ, объект или ситуация.

Фрейм отражает основные свойства объекта или явления. Информация в фреймах записывается в виде списка свойств, называемых во фрейме слотами (slot – паз, щель), таким образом, слот является основной структурной единицей фрейма.

Пример. Слова «комната» порождает у слушателя образ комнаты «жилое помещение» с четырьмя стенами, окнами и дверью, площадью 12-30 м². Из этого описания ничего нельзя убрать (убрав окна, получаем чулан), но в нем есть «дырки» или «слоты» - это незаполненные значения некоторых атрибутов. Например, количество окон, высота потолка и т.п. В теории фреймов такой образ называется фреймом комнаты.

Слот представляет собой пару: имя слота и его значение. В качестве значения слота могут выступать константы (факты), выражения с переменными, ссылки на другие слоты и т.п.

Слот может иметь структуру, элементы которой сами являются слотами. Фрейм состоит из конечного значения слотов. Слотам фреймов могут быть приписаны по умолчанию некоторые стандартные значения. Значения, присвоенные по умолчанию, могут быть заменены значениями, подходящими для обрабатываемой ситуации.

Различают фреймы-образцы или прототипы, хранящиеся в базе знаний, и фреймы-экземпляры, которые создаются для отображения реальных фактических ситуаций на основе поступающих данных. Фрейм-прототип – это интенсиональное описание некоторого множества фреймов-примеров.

Пример фрейма-прототипа: ДАТА

(ДАТА) (месяц)(имя)(день)(целые числа){1,2…31}(год)(функция) (день недели)(перечень {понед.,….,воскр.} (функция)

В слоте (месяц) на месте значения записано ИМЯ, т.е. значением слота может быть любое буквенное выражение. Значение слота ДЕНЬ являются целые числа, причем перечень их приводится в слоте.

В качестве функции могут быть использованы любые функции языка LISP. Так, в слоте ГОД с использованием языка LISP могут быть организованы следующие процедуры. Если во входном предложении указан ГОД, то он вносится в поле значения фрейма-примера; если год не указан, то активизируется процедура, которая заполняет значение текущим годом. Такого рода функция называется «по умолчанию».

В слоте «день недели» можно организовать процедуры, которые при обработке входного сообщения будут вызываться автоматически, для проверки на непротиворечивость значения дня недели, указанного пользователем, либо вычисления этого значения.

Конкретный пример может выглядеть следующим образом:

(ISA) ДАТА)(месяц)(июнь)(день)(вторн.)

Метка ISA обозначает, что данный слот является фреймом-примером.

Модель фрейма является достаточно универсальной, т.к. существуют не только фреймы для обозначения объектов и понятий, но и другие типы:

- фреймы-сценарии, используемые для обозначения объектов и понятий (лекция, собрание, заем);

- фреймы-роли (отец, мать, менеджер, кассир, клиент);

- фреймы-сценарии (собрание акционеров, празднование дня рождения)ж

- фреймы-ситуации (тревога, авария, рабочий режим работы устройства) и другие.

Формально как модуль для отображения образа структура фрейма может быть представлена следующим образом:

(имя фрейма)

(имя 1-го слота); (значение 1-го слота)

(имя 2-го слота); (значение 2-го слота)

………………………………………….

………………………………………….

(имя N-го слота); (значение N-го слота)

Ту же запись можно представить в виде таблицы

Имя фрейма
Имя слота	Значение слота	Способ получения слота	Присоединенная процедура

Иногда применяют другой вариант:

Имя фрейма
Имя слота	Указатель типа данных	значение слота	Присоединенная процедура

Значения столбцов этой таблицы: