Навигация
Вычислить значения параметров ПИ – регулятора, обеспечивающих устойчивость и установившуюся ошибку в системе = 0,06 при g(t)=2t и f(t)=0
6. Вычислить значения параметров ПИ – регулятора, обеспечивающих устойчивость и установившуюся ошибку в системе = 0,06 при g(t)=2t и f(t)=0

Поскольку возмущение f(t)=0, то ![]() . Найдем
. Найдем ![]() :
:
для этого найдем передаточную функцию замкнутой системы по каналу g-E
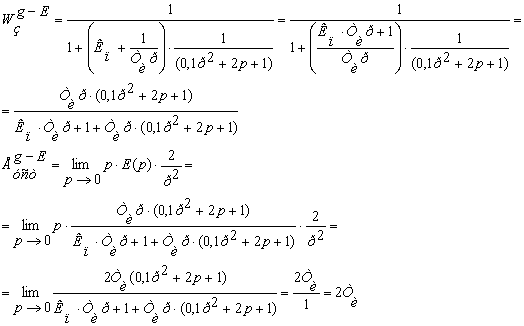
По условию ![]() , тогда подставим это значение в получившееся выражение:
, тогда подставим это значение в получившееся выражение:
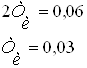
Таким образом для получения в системе установившейся ошибке равной 0,06 необходимо задать параметру постоянной времени значение 0,03.
7. Для интегрального закона регулирования и начальных условий ![]() , выбрать оптимальное значение постоянной времени регулятора по критерию:
, выбрать оптимальное значение постоянной времени регулятора по критерию: ![]() (Рассматривается движение в системе при g(t)=f(t)=0 и ненулевых начальных условиях).
(Рассматривается движение в системе при g(t)=f(t)=0 и ненулевых начальных условиях).
Для решения мы будем использовать метод Мондельштама. Для этого нам необходимо найти передаточную функцию замкнутой системы и взять характеристическое уравнение:

Получаем уравнение:
![]()
Поочередно умножаем его на ![]() и на Е
и на Е

Интегрируем полученное уравнение по частям

Получаем:
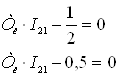

Интегрируем полученное уравнение по частям

Получаем:
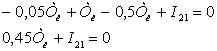
Из полученных уравнений составим систему уравнений:
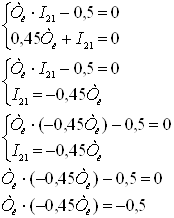
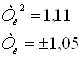
Выбираем ![]() =1,054
=1,054
8. Для найденного в пункте 7 значения постоянной времени регулятора построить с помощью ЭВМ вещественную частотную характеристику P(ω), приняв входным воздействием g(t) и входной координатой E(t)/
Для нахождения вещественной характеристики нам понадобится передаточная функция замкнутой системы по каналу g-y.

Перейдем в частотную область p=jω:

Домножаем на сопряженное знаменателю число и получаем:

Отделяем действительную часть U(ω):
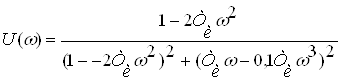
При ![]() =1,054
=1,054
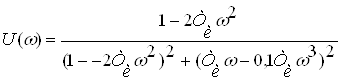
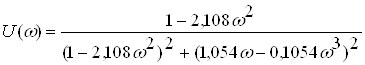
| w | p(w) |
| 0 | 1 |
| 0,1 | 1,010058 |
| 0,2 | 1,039191 |
| 0,3 | 1,079471 |
| 0,4 | 1,099022 |
| 0,5 | 0,997092 |
| 0,6 | 0,58593 |
| 0,7 | -0,06976 |
| 0,8 | -0,48243 |
| 0,9 | -0,56794 |
| 1 | -0,5208 |
| 1,1 | -0,44696 |
| 1,2 | -0,3782 |
| 1,3 | -0,32081 |
| 1,4 | -0,27428 |
| 1,5 | -0,23666 |
| 1,6 | -0,20606 |
| 1,7 | -0,18095 |
| 1,8 | -0,16013 |
| 1,9 | -0,14269 |
| 2 | -0,12796 |
| 2,5 | -0,08003 |
| 3 | -0,05481 |
| 3,5 | -0,03991 |
| 4 | -0,03037 |
| 4,5 | -0,02389 |
| 5 | -0,01929 |
| 5,5 | -0,0159 |
| 6 | -0,01334 |

9. По вещественной характеристике P(ω) пункта 8 построить переходной процесс E(t) при единичном ступенчатом изменении g(t) и нулевых начальных условиях методом трапециидальных частотных характеристик.
Для построения переходного процесса нам необходимо разбить получившуюся вещественную характеристику на трапеции и построить переходный процесс для каждой из полученных трапеций.
| R(0) | Wo | Wd | æ | ||
| I | - | 0,099021688 | 0,38 | 0,1 | 0,263158 |
| II | + | 1,666965285 | 0,88 | 0,43 | 0,488636 |
| III | - | 0,567943597 | 6 | 0,95 | 0,158333 |
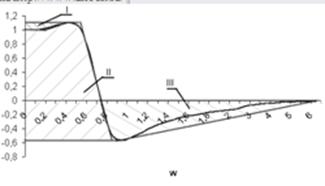
1-я трапеция
| t табл | h(æ) | t=t табл/Wo | h=R(0)*h(æ) |
| 0 | 0 | 0 | 0 |
| 0,5 | 0,199 | 1,315789474 | -0,019705316 |
| 1 | 0,386 | 2,631578947 | -0,038222372 |
| 1,5 | 0,56 | 3,947368421 | -0,055452145 |
| 2 | 0,709 | 5,263157895 | -0,070206377 |
| 2,5 | 0,833 | 6,578947368 | -0,082485066 |
| 3 | 0,928 | 7,894736842 | -0,091892127 |
| 3,5 | 0,994 | 9,210526316 | -0,098427558 |
| 4 | 1,039 | 10,52631579 | -0,102883534 |
| 4,5 | 1,057 | 11,84210526 | -0,104665924 |
| 5 | 1,067 | 13,15789474 | -0,105656141 |
| 5,5 | 1,067 | 14,47368421 | -0,105656141 |
| 6 | 1,054 | 15,78947368 | -0,104368859 |
| 6,5 | 1,043 | 17,10526316 | -0,103279621 |
| 7 | 1,035 | 18,42105263 | -0,102487447 |
| 7,5 | 1,025 | 19,73684211 | -0,10149723 |
| 8 | 1,024 | 21,05263158 | -0,101398209 |
| 8,5 | 1,022 | 22,36842105 | -0,101200165 |
| 9 | 1,025 | 23,68421053 | -0,10149723 |
| 9,5 | 1,027 | 25 | -0,101695274 |
| 10 | 1,027 | 26,31578947 | -0,101695274 |
| 10,5 | 1,028 | 27,63157895 | -0,101794295 |
| 11 | 1,025 | 28,94736842 | -0,10149723 |
| 11,5 | 1,021 | 30,26315789 | -0,101101144 |
| 12 | 1,015 | 31,57894737 | -0,100507013 |
| 12,5 | 1,01 | 32,89473684 | -0,100011905 |
| 13 | 1,005 | 34,21052632 | -0,099516797 |
| 13,5 | 1 | 35,52631579 | -0,099021688 |
| 14 | 0,997 | 36,84210526 | -0,098724623 |
| 14,5 | 0,996 | 38,15789474 | -0,098625601 |
| 15 | 0,995 | 39,47368421 | -0,09852658 |
| 15,5 | 0,995 | 40,78947368 | -0,09852658 |
| 16 | 0,995 | 42,10526316 | -0,09852658 |
| 16,5 | 0,995 | 43,42105263 | -0,09852658 |
| 17 | 0,995 | 44,73684211 | -0,09852658 |
| 17,5 | 0,995 | 46,05263158 | -0,09852658 |
| 18 | 0,995 | 47,36842105 | -0,09852658 |
| 18,5 | 0,994 | 48,68421053 | -0,098427558 |
| 19 | 0,992 | 50 | -0,098229515 |
| 19,5 | 0,991 | 51,31578947 | -0,098130493 |
| 20 | 0,991 | 52,63157895 | -0,098130493 |
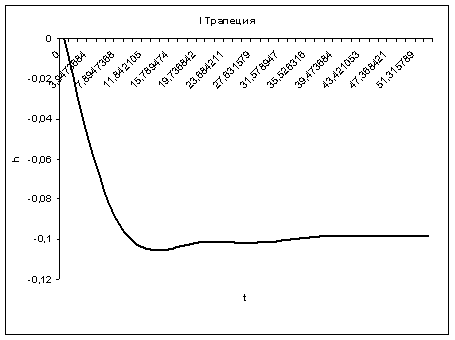
2-я трапеция
| t табл | h(æ) | t=t табл/Wo | h=R(0)*h(æ) | |
| 0 | 0 | 0 | 0 | |
| 0,5 | 0,24 | 0,568181818 | 0,400071669 | |
| 1 | 0,461 | 1,136363636 | 0,768470997 | |
| 1,5 | 0,665 | 1,704545455 | 1,108531915 | |
| 2 | 0,833 | 2,272727273 | 1,388582083 | |
| 2,5 | 0,967 | 2,840909091 | 1,611955431 | |
| 3 | 1,061 | 3,409090909 | 1,768650168 | |
| 3,5 | 1,115 | 3,977272727 | 1,858666293 | |
| 4 | 1,142 | 4,545454545 | 1,903674356 | |
| 4,5 | 1,138 | 5,113636364 | 1,897006495 | |
| 5 | 1,118 | 5,681818182 | 1,863667189 | |
| 5,5 | 1,092 | 6,25 | 1,820326092 | |
| 6 | 1,051 | 6,818181818 | 1,751980515 | |
| 6,5 | 1,018 | 7,386363636 | 1,696970661 | |
| 7 | 0,993 | 7,954545455 | 1,655296528 | |
| 7,5 | 0,974 | 8,522727273 | 1,623624188 | |
| 8 | 0,966 | 9,090909091 | 1,610288466 | |
| 8,5 | 0,966 | 9,659090909 | 1,610288466 | |
| 9 | 0,97 | 10,22727273 | 1,616956327 | |
| 9,5 | 0,975 | 10,79545455 | 1,625291153 | |
| 10 | 0,982 | 11,36363636 | 1,63695991 | |
| 10,5 | 0,987 | 11,93181818 | 1,645294737 | |
| 11 | 0,993 | 12,5 | 1,655296528 | |
| 11,5 | 0,997 | 13,06818182 | 1,66196439 | |
| 12 | 0,997 | 13,63636364 | 1,66196439 | |
| 12,5 | 0,997 | 14,20454545 | 1,66196439 | |
| 13 | 0,997 | 14,77272727 | 1,66196439 | |
| 13,5 | 0,998 | 15,34090909 | 1,663631355 | |
| 14 | 1 | 15,90909091 | 1,666965285 | |
| 14,5 | 1,002 | 16,47727273 | 1,670299216 | |
| 15 | 1,005 | 17,04545455 | 1,675300112 | |
| 15,5 | 1,008 | 17,61363636 | 1,680301008 | |
| 16 | 1,011 | 18,18181818 | 1,685301904 | |
| 16,5 | 1,011 | 18,75 | 1,685301904 | |
| 17 | 1,012 | 19,31818182 | 1,686968869 | |
| 17,5 | 1,009 | 19,88636364 | 1,681967973 | |
| 18 | 1,008 | 20,45454545 | 1,680301008 | |
| 18,5 | 1,006 | 21,02272727 | 1,676967077 | |
| 19 | 1,001 | 21,59090909 | 1,668632251 | |
| 19,5 | 0,998 | 22,15909091 | 1,663631355 | |
| 20 | 0,996 | 22,72727273 | 1,660297424 | |
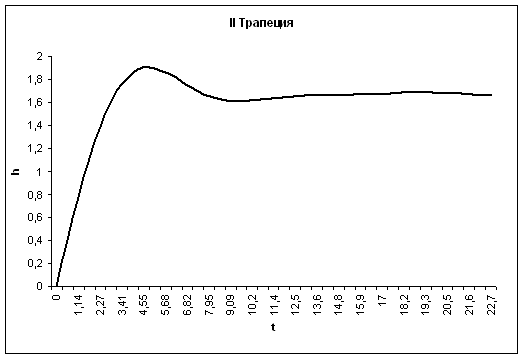
3-я трапеция
| t табл | h(æ) | t=t табл/Wo | h=R(0)*h(æ) |
| 0 | 0 | 0,0000 | 0,0000 |
| 0,5 | 0,184 | 0,0833 | -0,1045 |
| 1 | 0,256 | 0,1667 | -0,1454 |
| 1,5 | 0,516 | 0,2500 | -0,2931 |
| 2 | 0,655 | 0,3333 | -0,3720 |
| 2,5 | 0,833 | 0,4167 | -0,4731 |
| 3 | 0,863 | 0,5000 | -0,4901 |
| 3,5 | 0,928 | 0,5833 | -0,5271 |
| 4 | 0,974 | 0,6667 | -0,5532 |
| 4,5 | 0,977 | 0,7500 | -0,5549 |
| 5 | 1,012 | 0,8333 | -0,5748 |
| 5,5 | 1,019 | 0,9167 | -0,5787 |
| 6 | 1,013 | 1,0000 | -0,5753 |
| 6,5 | 1,009 | 1,0833 | -0,5731 |
| 7 | 1,006 | 1,1667 | -0,5714 |
| 7,5 | 1,006 | 1,2500 | -0,5714 |
| 8 | 1,008 | 1,3333 | -0,5725 |
| 8,5 | 1,01 | 1,4167 | -0,5736 |
| 9 | 1,016 | 1,5000 | -0,5770 |
| 9,5 | 1,022 | 1,5833 | -0,5804 |
| 10 | 1,025 | 1,6667 | -0,5821 |
| 10,5 | 1,028 | 1,7500 | -0,5838 |
| 11 | 1,029 | 1,8333 | -0,5844 |
| 11,5 | 1,027 | 1,9167 | -0,5833 |
| 12 | 1,025 | 2,0000 | -0,5821 |
| 12,5 | 1,022 | 2,0833 | -0,5804 |
| 13 | 1,019 | 2,1667 | -0,5787 |
| 13,5 | 1,017 | 2,2500 | -0,5776 |
| 14 | 1,016 | 2,3333 | -0,5770 |
| 14,5 | 1,015 | 2,4167 | -0,5765 |
| 15 | 1,014 | 2,5000 | -0,5759 |
| 15,5 | 1,014 | 2,5833 | -0,5759 |
| 16 | 1,014 | 2,6667 | -0,5759 |
| 16,5 | 1,014 | 2,7500 | -0,5759 |
| 17 | 1,013 | 2,8333 | -0,5753 |
| 17,5 | 1,012 | 2,9167 | -0,5748 |
| 18 | 1,011 | 3,0000 | -0,5742 |
| 18,5 | 1,009 | 3,0833 | -0,5731 |
| 19 | 1,008 | 3,1667 | -0,5725 |
| 19,5 | 1,006 | 3,2500 | -0,5714 |
| 20 | 1,005 | 3,3333 | -0,5708 |
| 20,5 | 1,004 | 3,4167 | -0,5702 |
| 21 | 1,003 | 3,5000 | -0,5696 |
| 21,5 | 1,003 | 3,5833 | -0,5696 |
| 22 | 1,002 | 3,6667 | -0,5691 |
| 22,5 | 1,002 | 3,7500 | -0,5691 |
| 23 | 1,002 | 3,8333 | -0,5691 |
| 23,5 | 1,002 | 3,9167 | -0,5691 |
| 24 | 1,001 | 4,0000 | -0,5685 |
| 24,5 | 1 | 4,0833 | -0,5679 |
| 25 | 1 | 4,1667 | -0,5679 |
| 25,5 | 0,999 | 4,2500 | -0,5674 |
| 26 | 0,999 | 4,3333 | -0,5674 |
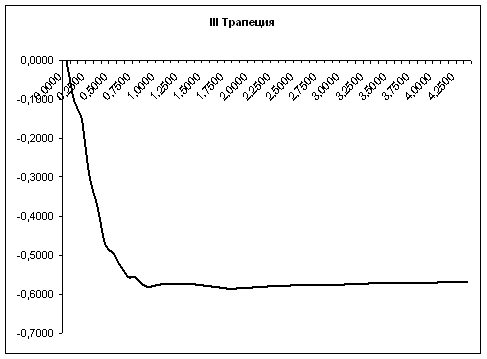
Суммируем графически полученные процесы и получаем
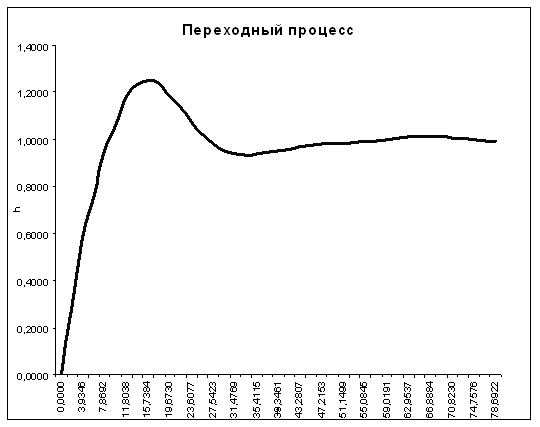
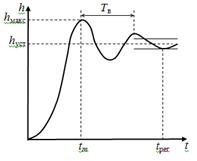
10. Определить время регулирования и максимальное перерегулирование в системе.
![]()

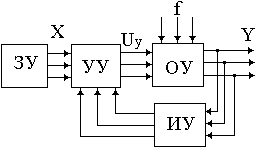
11. Разработать и начертить структурную схему комбинированной САУ, инвариантной по отношению к контролируемому возмущению ![]() .
.
Привести передаточную функцию устройства управления.
Проверить выполнение условия инвариантности.
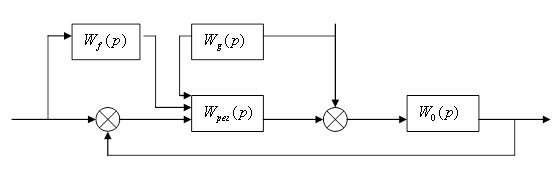
Условия инвариантности:
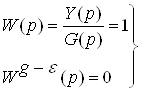 , если
, если ![]()
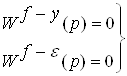 , если
, если ![]()
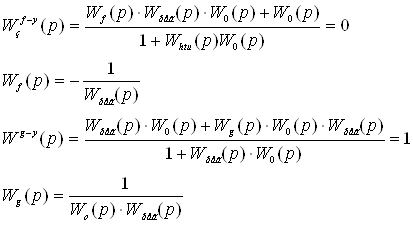
При выборе корректирующих звеньев в виде обратных передаточных функций возникает проблема. Она обычно связана с тем, что порядок числителя корректирующего звена становится больше порядка знаменателя. Это означает, что частотные характеристики таких звеньев являются расходящимися, что говорит о том, что физически такие звенья нереализуемы. В тех случаях, когда корректирующие звенья применять необходимо, порядок числителя этих звеньев искусственно приравнивают к порядку знаменателя, отбрасывая в числители высшие порядки.
12. Предложить и обосновать методы компенсации действия неконтролируемых возмущений, если известен класс функций, которыми они описываются.
астатический автоматический управление моделирование программа
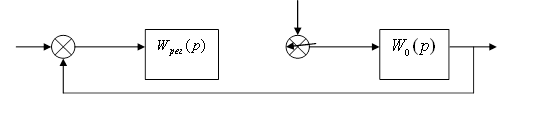
Решить проблему инвариантности можно, если известна предварительная информация о классе возмущающих воздействий. В частности, если известен математический аппарат, описывающий функцию f(t), заданный в виде решения некоторого дифференциального уравнения.
Процедура синтеза предусматривает:
1. восстановление вида дифференциального уравнения по заданному решению;
2. получение характеристического уравнения;
3. выбор передаточной функции регулятора, в которой знаменатель совпадает с видом полученного характеристического уравнения. Числитель передаточной функции регулятора выбирается того же порядка, что и знаменатель;
4. неизвестные коэффициенты числителя передаточной функции регулятора определяются из условий устойчивости замкнутой системы.
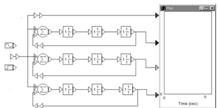
13. Провести моделирование в программе MatLab. Определить настройки регулятора, обеспечивающего минимизацию времени регулирования.
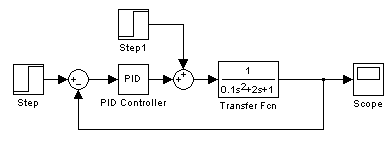
При нулевом задающем воздействии со значением регулятора, полученными в 7 пункте:
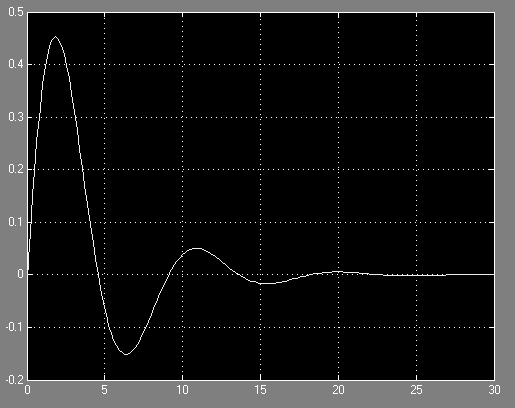
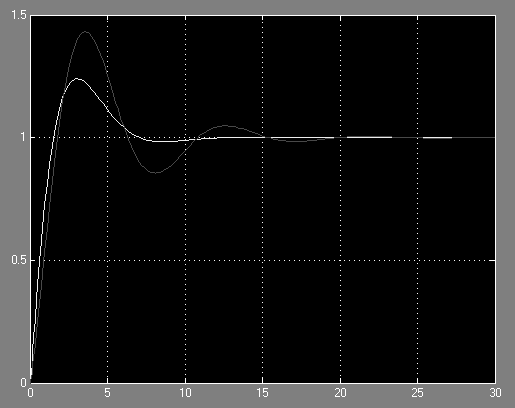
При единичном задающем воздействии:

Для снижения времени регулирования можно немного увеличить значения регулятора ![]() примерно до 1,085.
примерно до 1,085.
Так же значительно уменьшает время регулирование и ![]() введение пропорциональной составляющей, т.е. использование ПИ – регулятора. С его помощью легко можно уменьшить время регулирования примерно в 1,7 раза.
введение пропорциональной составляющей, т.е. использование ПИ – регулятора. С его помощью легко можно уменьшить время регулирования примерно в 1,7 раза.
Список используемой литературы
· Лекции по курсу ТАУ, Румянцев Ю.Д.
· "Теория автоматического управления", Воронов А.А.
· "Теория систем автоматического управления", Бесекерский В.А.
Приложение
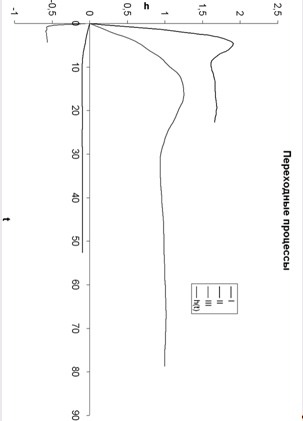
Похожие работы
... частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения ...
... значениях функции. Начальное значение функции:. (2.10) Конечное значение функции: . (2.11) 7. Теорема запаздывания . (2.12) 4. Дифференциальные уравнения САУ При математическом описании систем автоматического управления составляют уравнения статики и динамики. Уравнения статики описывают установившиеся режимы и, как правило, являются алгебраическими. Уравнения динамики ...
... главную регулируемую обратную связь и дополнительные обратные связи. 1 ФУНКЦИОНАЛЬНАЯ СХЕМА ОБЪЕКТА УПРАВЛЕНИЯ В качестве объекта управления используется управляемый полупроводниковый выпрямитель, двигатель постоянного тока независимого возбуждения типа 2ПН-132МУХЛ4. Вал двигателя соединен с тахогенератором. Выписываем из справочника параметры двигателя: Pн=2,5кВт Nн=1000 об¤мин; Nм=4000 ...
... состоит в построении системы управления; в нее входит выбор схемы управляющих устройств, элементов и их параметров, соединение автоматизированной и неавтоматизированной части, реализующих информационную технологию управления. Специфика построения систем организационного управления, где основным элементом объекта управления и управляющей части выступает управленческий персонал, рассматривается в ...




0 комментариев