Вивчення закономірностей ряду динаміки

4. Вивчення закономірностей ряду динаміки

 

Одним з найважливіших завдань аналізу рядів динаміки є виявлення і вивчення закономірностей у розвитку суспільних явищ і процесів, тобто встановлення загальної тенденції ряду динаміки та її характеру.

Під загальною тенденцією ряду динаміки (трендом) розуміють тенденцію зміни у певному напрямку рівня ряду динаміки. Загальна тенденція може мати вираження рівнів ряду у вигляді або сталих величин, або їх неухильної зміни в бік зменшення чи зростання. Характер ряду динаміки – це те, яким чином відбуваються ці зміни: за рівняннями прямої лінії або якоїсь кривої.

Загальну тенденцію ряду динаміки можна виявити шляхом огляду рівнів ряду динаміки. Найчастіше для цього використовується графічний спосіб.

Іноді необхідна істотна перебудова рівнів ряду. Найчастіше це відбувається тоді, коли рівні ряду під дією багатьох випадкових і короткочасних обставин, мають коливання, які ускладнюють аналіз показників ряду динаміки. В таких випадках статистика застосовує різні прийоми перебудови рядів динаміки з метою виявлення прихованих закономірностей, які неможливо виявити візуально. Головні із цих методів – укрупнення інтервалів, обчислення ковзної середньої, аналітичне вирівнювання.

Найпростіший метод – укрупнення інтервалів (періодів) – це перехід від первинних даних до укрупнених даних за більший відрізок часу. Наприклад, якщо ми маємо первинні дані за кожний окремий місяць, то їх можна замінити даними за квартал, півріччя або рік. Таке укрупнення інтервалів провадиться поступово: від малих до все більших інтервалів, поки загальна тенденція ряду динаміки не стане досить чіткою. Але слід відзначити, що застосування цього способу можливо лише при рівності порівнювальних інтервалів. При даному способі кількість членів ряду динаміки значно скорочується, а також випадають з поля зору рух рівнів ряду динаміки усередині цього укрупненого періоду. Укрупнені періоди обов`язково характеризуються середніми рівнями ряду.

В табл. 6 наведені дані про кількість зареєстрованих злочинів по лінії карного розшуку для обчислення і виявлення загальної тенденції ряду динаміки.

В стовпчику 3 табл. 6 відмічено, що вирівнювання здійснюється за квартал. В стовпчику 4 цієї ж таблиці обчислено загальну кількість зареєстрованих злочинів за квартал. Після цього обчислюємо середню кількість зареєстрованих злочинів за кожний місяць протягом кварталу. Ця середня кількість обчислюється шляхом ділення загальної кількості на три місяця, тобто за середньою арифметичною простою. Дані, наведені в стовпчику 5 табл. 6, підкреслюють наявність деякої тенденції до зростання кількості зареєстрованих злочинів в IV кварталі року порівняно з І кварталом цього ж року.

Таблиця 6. Кількість зареєстрованих злочинів по місяцям

Місяць року	Кількість злочинів	Період укрупнення, квартал	Загальна кількість за період	Середня кількість за період	Ковзна середня за три місяці	Теоретична пряма, Уt
січень	31391				-	36695,12
лютий	38756	I	111706	37235,3	37235,3	37397,24
березень	41559				40961,7	38099,36
квітень	42570				41377,3	38801,48
травень	40003	ІІ	123221	41073,7	41073,7	39503,6
червень	40648				40573,3	40205,72
липень	41069				40256,0	40907,84
серпень	39051	ІІІ	120672	40224,0	40224,0	41609,96
вересень	40552				40254,7	42312,08
жовтень	41161				40389,3	43014,2
листопад	39455	IV	131082	43694,0	43694,0	43716,32
грудень	50466				-	44418,44

Значно більші можливості для аналізу ряду динаміки має застосування способу ковзної середньої. Сутність цього способу полягає в тому, що кожний рівень ряду динаміки замінюється середньою величиною, яка обчислюється з даного і сусідніх рядів. Цей спосіб одержав назву за техніку обчислення: кожна наступна середня величина обчислюється шляхом переміщення на один рівень ряду. В нашому прикладі спочатку обчислюється середній рівень за три місяці (січень, лютий, березень), а потім – за лютий, березень і квітень і т.п.

Результати обчислення ковзної середньої обов`язково відносяться до середини періоду, тому, як правило, її обчислюють з непарного числа рівнів ряду. Якщо період буде включати парну кількість рівнів ряду, то обчислені середні величини необхідно відносити до середини проміжку між двома рівнями ряду.

В стовпчику 6 табл. 6 наведено ковзну середню величину, яка обчислена за три місяці. З цих даних видно, що наприкінці року дійсно реєструється значно більше злочинів, ніж на початку. Можна обчислити ковзну середню і за більший проміжок часу. Існує думка, згідно з якою чим більший проміжок часу береться за інтервал для обчислення ковзної середньої величини, тим більш зрозумілою стає загальна тенденція ряду динаміки, але в той же час завжди скорочується кількість рівнів на величину: тривалість інтервалу вирівнювання мінус одиниця. Стовпчик 6 табл. 6 дійсно коротший на два рівня, ніж первинні дані, тому що інтервал вирівнювання дорівнює трьом (3 – 1), тобто зникають один рівень на початку ряду динаміки і один наприкінці.

До недоліків згладжування ряду динаміки способом ковзної середньої відносяться:

 1) неможливість обчислення показників для початкових і останніх рівнів ряду,

2) довільність вибору інтервалу згладжування, що може істотно впливати на одержані результати. Тому цей спосіб використовується з метою попередньої оцінки наявності чи відсутності загальної тенденції зміни рівнів ряду динаміки.

Найбільш досконалим способом для виявлення загальної тенденції та її характеру є аналітичне вирівнювання рядів динаміки. Аналітичне вирівнювання – це основа для використання інших методів поглибленого вивчення рядів динаміки з метою проведення статистичного аналізу взаємозв`язків між явищами.

Сутність аналітичного вирівнювання – це знаходження такого математичного вираження закономірностей (рівняння прямої лінії, гіперболи параболи або якоїсь іншої). Знаходять таке рівняння, яке максимально наближуватиметься до первинних даних Наприклад, на графіку (рис. 2) наносимо первинні дані (табл. 6), ковзну середню і побудуємо теоретичну пряму лінію, яка з точки зору математики найбільш близько підходить до первинних даних. У математиці з цією метою застосовується спосіб найменших квадратів, за допомогою якого визначають параметри аналітичного рівняння обраної лінії, тобто щоб сума квадратів відхилень фактичних рівнів від вирівняних, які розташовані на теоретичній лінії, була б найменшою.

Технічно вирівнювання зводиться до заміни фактичних рівнів ряду такими, які б у середньому найменше за все відхилялися від фактичних, які б мали певне аналітичне вираження. За даними, наведеними в табл. 6, побудуємо теоретичну лінію у вигляді рівняння:

У_t= а₀ +а₁t,

де: У_t – теоретична лінія значень; а₀ ,а₁ – параметри теоретичної лінії;

t – час, порядкові номери періодів або моментів часу (абсциси точок прямої).

Параметри а₀ таа₁ теоретичної прямої, яку ми повинні знайти, з урахуванням вимог методів найменших квадратів, знаходяться шляхом розв`язуванням системи рівнянь:

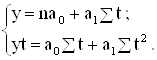
В цій системі рівнянь у – фактичні рівні ряду динаміки, n – кількість рівнів ряду динаміки (у нашому прикладі їх 12).

Розв`язавши цю систему рівнянь, знаходимо, що теоретична лінія буде мати вигляд:

У_t= 35993+702,12t.

Результати вирівняних рівнів, одержані внаслідок такого вирівнювання вихідних даних наведені в останньому стовпчику табл. 20.

Після усіх проведених розрахунків побудуємо ці дані у вигляді графіку (рис. 2).

прогнозування динаміка статистичні ряди

Місяць

Рис. 2 Кількість зареєстрованих злочинів по місяцях

Умовні позначення:

- вихідні дані;
- ковзна середня;
- вирівняна пряма.

Проведене аналітичне вирівнювання на основі прямої лінії дає змогу лише виявити основну закономірність зміни явища. З точки зору математичного аналізу можна застосовувати показові функції та параболи 2-го порядку. Застосування сучасної обчислювальної техніки значно спрощує техніку обчислення, але підвищує вимоги до рівня дослідника, який повинен мати більш чітке уявлення про наявність і форму зв`язку між явищами.

Щорічні рівні більшості суспільних, особливо правових явищ залежать від сезонних коливань. Перебудова рівнів ряду динаміки застосовується для їх виявлення і обчислення індексів сезонності. Індекс сезонності – це відношення кожного рівня ряду динаміки у вигляді відсоткового відношення рівнів кожного місяця до якогось теоретичного, як правило, середнього рівня за рік, який приймається за базу порівняння. Розрахунок можна представити у вигляді формули:

І_с = . 100, або І_с = . 100 ,

де: І_с – індекс сезонності; у_і – фактичні щомісячні рівні ряду;  – вирівняні рівні (рівні теоретичної лінії);  – середня величина із щомісячних рівнів ряду.

Для більшої надійності одержаних результатів індекси сезонності обчислюються за даними за три роки (або більший період часу). В цьому випадку для кожного місяця обчислюється середня величина рівня за три роки, яка і порівнюється з загальним середньомісячним рівнем за три роки або для кожного року окремо обчислюються щомісячні індекси сезонності, з яких потім обчислюється середній рівень для кожного місяця.

Існують і інші більш складні методи обчислення індексів сезонності.

Сезонні коливання властиві абсолютній більшості юридичних явищ. Тому їх аналіз має велике значення для планування заходів протидії злочинності, прийняття відповідних управлінських рішень, вирішення питань оперативного і матеріально-технічного забезпечення діяльності правоохоронних органів.

5. Інтерполяція, екстраполяція та прогнозування в рядах динаміки

Вивчення рядів динаміки різних суспільних явищ дає базу для прогнозування і для знаходження невідомих рівнів ряду.

Інтерполяція – це спосіб побудови рядів динаміки за попередній період, коли з якихось причин були відсутні відомості про розміри явища, або для знаходження невідомих проміжних рівнів ряду динаміки. Відсутність цих даних може бути обумовлена різними причинами: був відсутній облік цих явищ в попередній час, змінилася методика обчислення показника тощо. Для того щоб обчислити невідомі рівні ряду динаміки, провадять математичні розрахунки різної складності.

Невідомі рівні ряду динаміки знаходять або на базі сусідніх відомих значень ряду динаміки шляхом обчислення їх середньої арифметичної простої, або на базі взаємозв`язку цього явища з іншими, кількісний вираз яких відомий. При застосуванні методу інтерполяції робиться припущення, що загальна тенденція, яку ми маємо зараз, мала місце і в попередній інтервал часу. Завжди при застосуванні цього методу проводяться математичні розрахунки різної складності.

Наприклад, таким чином можна обчислити населення країни протягом року, тому що офіційна статистика обов`язково наводить дані лише на початок кожного року.

Інтерполяція дає змогу приблизно відобразити ті закономірності, які склалися протягом певного періоду.

Екстраполяція – це спосіб продовження кількісних характеристик сукупностей за межі досліджуваного явища в майбутнє на базі встановлених закономірностей за попередній термін. За допомогою способу екстраполяції можуть бути зроблені висновки, одержані внаслідок вивчення однієї частини сукупності та поширені на його іншу аналогічну частину.

В основі використання способу екстраполяції лежить припущення, що фактори, які обумовили розвиток даного явища, залишаються незмінними і протягом наступного періоду. Цей спосіб в останні роки найчастіше застосовується для прогнозування явищ лише на короткий проміжок часу.

Використовуючи спосіб екстраполяції, можна прогнозувати чисельність населення, його міграцію, а також зміни в правових явищах.

Для екстраполяції найчастіше застосовують аналітичний спосіб вирівнювання ряду динаміки. За даними, які наведені в табл. 6, можна спрогнозувати, чому буде дорівнювати кількість зареєстрованих злочинів в перший місяць наступного року. Для цього у формулу: У_t= 35993+702,12t, підставимо t, яке дорівнює 13. Одержимо, що кількість їх складе 45121 злочин. Коли будемо мати первинні дані, то можна порівняти, наскільки буде відрізнятися наш рівень прогнозу від реальної кількості зареєстрованих злочинів.

Можливе і таке обчислення наступних рівнів ряду динаміки: кінцевий рівень помножують на середній темп зростання.

Методи інтерполяції і екстраполяції в статистиці застосовують для прогнозування, планування та кореляційного аналізу розвитку правових явищ. Використання цих способів можливо лише тоді, коли явища змінюються стабільно. Вперше в розвитку науки на можливість спрогнозувати показники статистичних рядів на нетривалий період звернув увагу А.Кетле, який з великою достовірністю спрогнозував кількість вчинених злочинів у Франції в 1830 р. на базі статистичних даних 1829 р. На цьому ґрунті пізніше з`явилась теорія усталеності статистичних рядів В.Лексиса.

Тому при прогнозуванні на тривалий час ми завжди повинні використовувати методи інтерполяції і екстраполяції в сукупності з іншими методами, такими як метод експертних оцінок, математичного модулювання і т. п.

Список літератури

 

1.  Лунеев В.В. Юридическая статистика: Учебник. – М.: Юристъ, 2009. – 400 с.

2.  Постанова Кабінету Міністрів України “Про порядок ведення спеціальної митної статистики” від 12 грудня 2002 р. № 1865. // Урядовий кур`єр 19.12. 2002. – с. 20.

3.  Правова статистика: Навч. посібник /О.Г. Кальман, І.0. Христич. – Х.: “Право”, 2008. – 204 с.

4.  Правова статистика. Курс лекцій./ О.М. Джужа, Ю.В. Александров, В.В. Василевич та інші. Під заг. ред. О.М. Джужи. – К.: [НАВСУ: Правові джерела], 2007. – 336 с.

5. Савюк Л.К. Правовая статистика: Учебник. – М.: Юристъ, 2009. – 588 с.

6. Словарь криминологических и статистических терминов. // Кальман А.Г., Христич И.А. – Х.: ИИПП АПрН Украины, изд-во “Гимназия”, 2008. – 96 с.

7. Статистика: Підручник/За ред, А.В. Головача, А.М. Єріної, О.В. Козирєва. - К.: Вища шк., 2008. – 623 с.

8. Статистика: Підручник/ С.С. Герасименко, А.В. Головач, А.М. Єріна та ін.; За наук. ред. д-ра екон. наук С.С. Герасименка. – 2-ге вид., перероб. і доп. – К.: КНЕУ, 2007. – 467 с.

9. Статистичний облік і звітність у правоохоронних органах України// Кальман О.Г., Христич І.О. Науково-практичний посібник. – Х.: ІВПЗ АПрН УКраїни, вид-во “Гимназия”, 2008. – 140 с.

10. Трофімова Г.Г. Правова статистика: Навч.-метод. посібник для самост. вивч. дисц. – К.: КНЕУ, 2006. – 75 с.

11. Чернадчук В.Д. Правовая статистика: конспект лекций. – К.: МАУП, 2009. – 72 с.