Навигация
Нахождение прогнозных значений методом наименьших квадратов
2.3 Нахождение прогнозных значений методом наименьших квадратов
демографический прогноз население численность
Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии.
Чем меньше расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии. Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Для нахождения прогнозных значений численности населения часто предполагается, что рост идет в геометрической прогрессии, и тогда сглаживание производится по показательной функции.
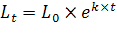 (4)
(4)
где ![]() - численность населения в прогнозный период;
- численность населения в прогнозный период; ![]() - численность населения в период, предшествующий прогнозному; е - основные натурального логарифма; k - общий коэффициент прироста населения, выраженный в долях единиц, рассчитанный по формуле:
- численность населения в период, предшествующий прогнозному; е - основные натурального логарифма; k - общий коэффициент прироста населения, выраженный в долях единиц, рассчитанный по формуле: 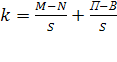 (5)
(5)
где M - число родившихся за период; N – число умерших за период; П- число прибывших за период; В – число выбывших за период; S – средняя численность населения за период; t- период, на который разрабатывается прогноз.
Согласно имеющимся данным, численность населения Оренбургской области на 1 января 2008 года составила 2 119 003 чел., на 1 января 2009 – 2 111 531 чел., за 2008 год родилось 26 947 чел., умерло 30 904 чел., 25 570 чел. прибыло и 29 085 чел. выбыло. Рассчитаем численность населения в 2010-2012 гг. при условии, что коэффициент общего прироста населения (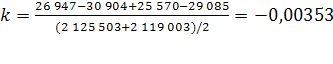 ) останется неизменным на всем протяжении прогнозных лет:
) останется неизменным на всем протяжении прогнозных лет:
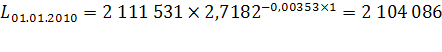 чел.
чел.
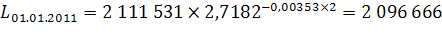 чел.
чел.
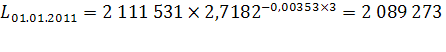 чел.
чел.
Сглаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой независимой переменной. Ясно, что развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Развитие явления во времени выступает как результат действия этих факторов.
Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых трудных задач предпрогнозного анализа.
Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле:
![]() (6)
(6)
где ![]() – фактические значения ряда динамики;
– фактические значения ряда динамики; ![]() – расчетные (сглаженные) значения ряда динамики; n – число уровней временного ряда; р – число параметров, определяемых в формулах, описывающих тренд.
– расчетные (сглаженные) значения ряда динамики; n – число уровней временного ряда; р – число параметров, определяемых в формулах, описывающих тренд.
С помощью программы Excel проверим предположение о том, что изменение численности населения в Оренбургской области, хорошо апроксимируется экспоненциальной линией тренда.
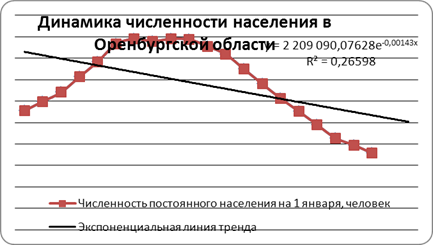
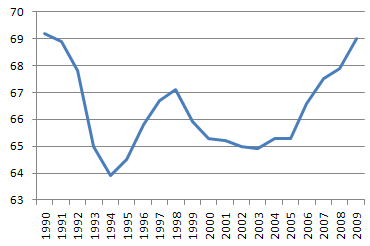
Рис. 1. Динамика численности населения в Оренбургской области с экспоненциальной линией тренда.
Видно, что разница между фактическими и сглаженными значениями данного ряда очень велика. Невысокий коэффициент достоверности аппроксимации также подтверждает, что использовать данный тип тренда нецелесообразно.
Наибольшее приближение к фактическим уровням данного динамического ряда дает функция полинома второй степени.
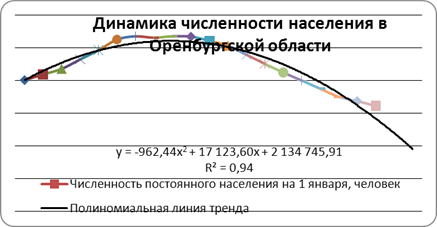
Рис. 2. Динамика численности населения в Оренбургской области с полиномиальной линией тренда.
При использовании уравнения полинома третьей степени, коэффициент аппроксимации увеличивается до 0,97, но при этом усложняется и сама модель, что может отрицательно сказаться на ее прогностических возможностях.
Уравнение регрессии примет вид:
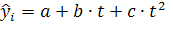 (7)
(7)
![]() - выровненные, т.е. лишенные колебаний, уровни тренда для лет с номером i; а - это средний (выровненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. t = 0; b - это средний за весь период среднегодовой прирост, который изменяется равномерно со средним ускорением, равным 2с; c- константа, главный параметр параболы II порядка.
- выровненные, т.е. лишенные колебаний, уровни тренда для лет с номером i; а - это средний (выровненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. t = 0; b - это средний за весь период среднегодовой прирост, который изменяется равномерно со средним ускорением, равным 2с; c- константа, главный параметр параболы II порядка.
Параметры a, b и c оцениваются методом наименьших квадратов и отвечают принципу максимального правдоподобия: сумма квадратов отклонений фактических уровней от тренда (от выровненных по уравнению тренда уровней) должна быть минимальной для данного типа уравнения.
На диаграмме уравнение тренда имеет вид: 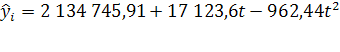 ,где
,где ![]() =0 в 1990г.
=0 в 1990г.
При этом нумерация периодов начинается с t=1. Однако рациональнее начало отсчета времени перенести в середину ряда, т.е. при нечетном п - на период (момент) с номером (п +1 )/2, а при четном числе уровней ряда - на середину между периодом с номером n/2 и (n/2)+1. Расчет параметров тренда при переносе отсчета времени на середину ряда приведен в приложении 3. Тогда уравнение тренда принимает вид: 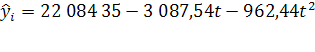 , где
, где ![]() =0,5 в 2000г.
=0,5 в 2000г.
За период 1990-2009г показатель численности населения в Оренбургской области убывал в номинальной оценке ускоренно, со средним ускорением 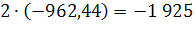 человек за год; средняя убыль населения за весь период составила 3 087 человек; средний уровень численности населения на середину периода был равен 22 084 35 чел.
человек за год; средняя убыль населения за весь период составила 3 087 человек; средний уровень численности населения на середину периода был равен 22 084 35 чел.
Для оценки надежности тренда необходимо оценить надежность его главного параметра – ускорения. Средняя ошибка репрезентативности выборочной оценки параметра с вычисляется по формуле:
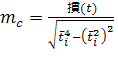 (8)
(8)
Где S(t) – оценка генерального показателя колеблемости, учитывающая потерю степеней свободы и определяемая по формуле 6.
Используя данные приложения 3, найдем искомые величины:
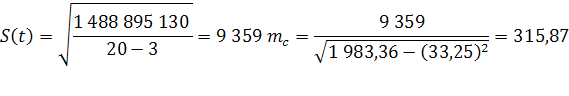
Отношение параметра с (половина ускорения) к его средней ошибке - это t-критерий Стьюдента: 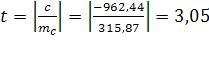
Табличное значение критерия Стъюдента 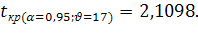 Фактическая величина критерия больше табличного, следовательно, вероятность нулевой гипотезы (о равенстве параметра с нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность населения Оренбургской области снижалась не случайно.
Фактическая величина критерия больше табличного, следовательно, вероятность нулевой гипотезы (о равенстве параметра с нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность населения Оренбургской области снижалась не случайно.
Прогноз по этой модели заключается в подстановке в уравнение тренда номера периода, который прогнозируется. Для 2010 года период времени t = 10,5, прогнозное значение составит:
![]() 2010=
2010=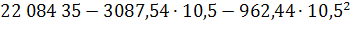 =2 069 907 чел.
=2 069 907 чел.
Полученное прогнозное значение является точечным и не учитывает колеблемость уровней показателя.
При прогнозе с учетом случайной колеблемости учитывается как вызванная колеблемостью ошибка репрезентативности выборочной оценки тренда, так и колебания уровней в отдельные периоды (моменты) относительно тренда.
Общая формула средней ошибки прогноза положения параболического тренда на период с номером ![]() от середины базы расчета тренда имеет вид:
от середины базы расчета тренда имеет вид:
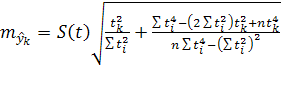 (9)
(9)
Средняя ошибка тренда на 2010 год равна:
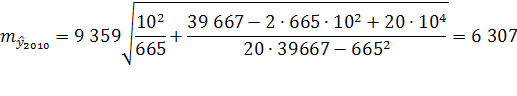
Вероятность того, что фактическая ошибка не превысит одного среднего квадратического отклонения, т.е. m равна при нормальном распределении 0,68. Чтобы получить доверительный интервал прогноза линии тренда с большей вероятностью, например с вероятностью 0,95,среднюю ошибку нужно умножить на величину t-критерия Стъюдента для вероятности 0,95 и n-p степеней свободы.
Получаем вероятную ошибку:
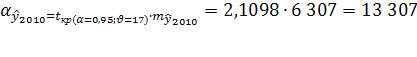
с вероятностью 95% можно утверждать, что тренд численности населения в Оренбургской области в 2010 году проходит в границах 2 069 907±13 307 или от 2 056 600 до 2 083 214 человек.
Определив ошибку репрезентативности выборочной оценки тренда, и колебания уровней в отдельные периоды (моменты) относительно тренда, получаем единую формулу средней ошибки прогноза конкретного отдельного уровня:
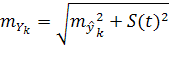 (10)
(10)
Для искомого прогнозного значения: 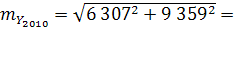 11 286
11 286 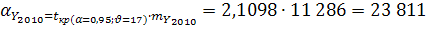 .
.
Таким образом, для прогнозного значения показателя численности населения на 1 января 2010 года определены границы доверительного интервала 2 046 096 – 2 093 718 человек.
Аналогично рассчитываем прогнозные значения на 2011-2012 годы:
![]() 2011=2 045 646 чел.
2011=2 045 646 чел. 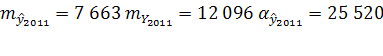
Доверительный интервал: (2 020 126; 2 071 166).
![]() 2012=2 019 459 чел.
2012=2 019 459 чел. 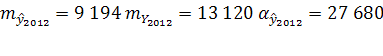
Доверительный интервал: (1 991 780; 2 047 138)
Средняя относительная ошибка 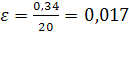 , что свидетельствует о высокой точности прогноза.
, что свидетельствует о высокой точности прогноза.
Расчет прогнозных значений для других показателей приведен в приложении 3, сведем полученные результаты в общую таблицу:
Таблица 5
Прогнозные значения абсолютных показателей родившихся и умерших, прибывших и выбывших в Оренбургской области, полученные методом наименьших квадратов.
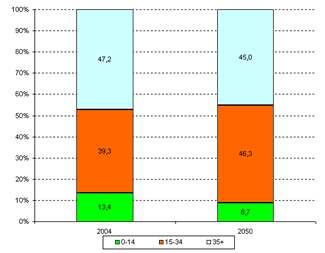
| Абсолютный показатель, человек | 2006 | 2007 | 2008 | Прогноз на 2009 | Прогноз на 2010 | Прогноз на 2011 | Δ |
| ε |
| Родившиеся | 23335 | 25776 | 26947 | 29 253 | 31 220 | 33 395 | 0 | 1135 | 4,13 |
| Умершие | 31 583 | 31 000 | 30 904 | 30 190 | 29 392 | 28 470 | 0 | 1420 | 3,69 |
| Абсолютный показатель, человек | 2007 | 2008 | 2009 | Прогноз на 2010 | Прогноз на 2011 | Прогноз на 2012 | Δ |
| ε |
| Прибывшие | 31 949 | 25 570 | 28 053 | 29 586 | 31 144 | 33 202 | 0,11 | 3499 | 7,68 |
| Выбывшие | 33 225 | 29 085 | 25 603 | 24 352 | 22 589 | 20 826 | 0 | 2437 | 5,17 |
Величины относительной ошибки свидетельствуют о высокой точности прогноза. По имеющимся данным видно, что при наметившихся тенденциях естественный прирост населения в прогнозируемые годы увеличится (увеличение рождаемости и снижение смертности), как и миграционный прирост.
Для сравнения полученных результатов составим сводную таблицу по всем применяемым методам:
| Численность постоянного населения на 1 января, человек | |||||||||
| МСС | МЭС | МНК | |||||||
| 2007 | 2 125 503 | 2 125 503 | 2 125 503 | ||||||
| 2008 | 2 119 003 | 2 119 003 | 2 119 003 | ||||||
| 2009 | 2 111 531 | 2 111 531 | 2 111 531 | ||||||
| прогноз | |||||||||
| 2010 | 2 116 188 | 2 164 883 | 2 069 907 | ||||||
| 2011 | 2 117 127 | 2 045 646 | |||||||
| 2012 | 2 115 261 | 2 019 459 | |||||||
| Ср. абсолют. оценка | 299 | -6064 | 0,38 | ||||||
| Ср. квадрат. оценка | 1 478 | 33749 | 8628 | ||||||
| Ср. относит. ошибка | 0,05 | 1,36 | 0,017 | ||||||
| Число родившихся, чел. | Число умерших, чел. | ||||||||
| МСС | МЭС | МНК | МСС | МЭС | МНК | ||||
| 2 006 | 23335 | 23335 | 23335 | 31 583 | 31 583 | 31 583 | |||
| 2 007 | 25776 | 25776 | 25776 | 31 000 | 31 000 | 31 000 | |||
| 2 008 | 26947 | 26947 | 26947 | 30 904 | 30 904 | 30 904 | |||
| прогноз | |||||||||
| 2 009 | 25 743 | 23 915 | 29 253 | 31 130 | 30 754 | 30 190 | |||
| 2 010 | 25 754 | 31 220 | 31 087 | 29 392 | |||||
| 2 011 | 26 125 | 33 395 | 31 026 | 28 470 | |||||
| Ср. абсолют. оценка | -85 | -135 | 0 | 32 | 64 | 0 | |||
| Ср. квадрат. оценка | 594 | 3 275 | 1135 | 795 | 2 571 | 1420 | |||
| Ср. относит. ошибка | 2 | 9,94 | 4,13 | 2,02 | 8,14 | 3,69 | |||
| Число прибывших, человек | Число выбывших, человек | ||||||||
| МСС | МЭС | МНК | МСС | МЭС | МНК | ||||
| 2007 | 31 949 | 31 949 | 31 949 | 33 225 | 33 225 | 33 225 | |||
| 2008 | 25 570 | 25 570 | 25 570 | 29 085 | 29 085 | 29 085 | |||
| 2009 | 28 053 | 28 053 | 28 053 | 25 603 | 25 603 | 25 603 | |||
| прогноз | |||||||||
| 2010 | 29 352 | 37 366 | 29 586 | 28 144 | 36311 | 24 352 | |||
| 2011 | 28 091 | 31 144 | 28 457 | 22 589 | |||||
| 2012 | 28 078 | 33 202 | 27 506 | 20 826 | |||||
| Ср. абсолют. оценка | 11 | -3539 | 0,11 | 32 | -2070 | 0 | |||
| Ср. квадрат. оценка | 2 177 | 15857 | 3499 | 1 161 | 8458 | 2437 | |||
| Ср. относит. ошибка | 5 | 35,27 | 7,68 | 2 | 20,04 | 5,17 | |||
Как видно из таблицы, значения средней квадратической оценки средней относительной ошибки у показателей минимальны для метода скользящей средней, и в целом данный метод дает хорошие результаты при прогнозировании демографических процессов. Кроме того, метод прост в использовании, что открывает широкие возможности для его применения. Метод наименьших квадратов более сложен в работе, но позволяет получить также достоверные результаты при условии подбора вида линии тренда, хорошо аппроксимирующей исходный динамический ряд.
Применение метода экспоненциального сглаживания целесообразно только при условии использования среднего уровня ряда в качестве начального значения экспоненциальной взвешенной. Но и в этом случае, полученные результаты являются самыми ненадежными по сравнению с прогнозированием другими методами.
Следует отметить, что прогнозирование методами экстраполяции основывается на использовании простого методологического аппарата и часто используется для получения будущих оценок социально-экономических процессов. Оправдано их использование и в частности при построении демографических прогнозов, поскольку процессы естественного и миграционного движения достаточно инерционны и не подвержены резким скачкам в уровнях.
Заключение
В соответствии с поставленными задачами в данной работе были исследованы 4 группы методов, используемых при прогнозировании демографических процессов:
1) методы экстраполяции;
2) экономико-математические методы, позволяющие разработать многофакторные динамические модели;
3) методы передвижки возрастов и когорт;
4) методы экспертных оценок.
Опираясь на имеющиеся в распоряжении данные, для практической части работы, была выбрана первая группа методов. В результате чего были построены прогнозные оценки показателей, характеризующих естественное и миграционное движения населения в Оренбургской области, с помощью трех методов экстраполяции:
- метод скользящей средней;
- метод экспоненциального сглаживания;
- метод наименьших квадратов.
Сравнив полученные результаты, сделаем вывод о целесообразности применения для прогнозирования метода скользящей средней и метода наименьших квадратов. Метод экспоненциального сглаживания позволил найти менее точные прогнозные оценки по сравнению с другими методами.
Метод наименьших квадратов позволил определить, что наилучшее приближение к исходным уровням временных рядов дает функция параболы II порядка для всех показателей, кроме «Числа выбывших, человек» - для него лучшей аппроксимацией является линейный тренд.
Для показателя «постоянного населения», «Число прибывших» и «Число выбывших» найдены прогнозные значения и определены границы доверительных интервалов на 2010, 2011,2012 годы.
Для показателей «Числа родившихся» и «Числа умерших» найдены прогнозные значения и определены границы доверительных интервалов на 2009, 2010,2011 годы.
Полученные абсолютные данные могут использоваться для формирования демографической политики, а также прогнозирования социально-экономических процессов.
Список использованных источников и литературы
1. Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование: Учебник. — М.: Финансы и статистика, 2001. — 228 с.
2. Артамонова И. А., Краснопевцева Б. В. Учебное пособие «Теория управления». Москва: МИИГАик, 2003.-86с.
3. Ахметов Р. Ш. Демографические процессы в Оренбургской области: вчера, сегодня, завтра – Региональный портал образовательного сообщества Оренбуржья http://www.orenport.ru/
4. Борисов В. А. Демография Учебник для вузов 2-е изд., исправленное— М.: Издательский дом NOTABENE, 1999, 2001. — 272 с.
5. Добров Г.М. Рабочая книга по прогнозированию. - М.: 1998
6. Концепция демографической политики Оренбургской области на период до 2025 года. Портал органов государственной власти Оренбуржья http://www.orenburggov.ru/magnoliaPublic/regportal/Info/SocialServices/dempolit/Main.html
7. Кузьмин А.И. Курс лекций "Основы демографии". Лекция 6 Основные показатели демографии. http://www.humanities.edu.ru/db/msg/47074
8. Курбатов В.И. Социальная работа: Учебное пособие. – М.: Издательско-торговая корпорация «Дашков и К», Ростов н/Д: Наука – Пресс, 2007 – 480с.
9. Луков В.А. Социальное проектирование. - М.: 1997. – 282 с.
10. Медков В. М. Демография: Учебное пособие. Серия «Учебники и учебные пособия». - Ростов-на-Дону: «Феникс», 2002. - 448 с.
11. Новикова Н.В., Поздеева О.Г. Прогнозирование национальной экономики: Учебно-методическое пособие. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2007. - с.138
12. Областной статистический ежегодник. 2009: Стат.сб./Территориальный орган Федеральной службы государственной статистики по Оренбургской области.- Оренбург. 2009. – 525 с.
13. Основы социальной работы: Учеб. пособие для студ. высш. учеб. заведений / Под ред. Н.Ф. Басова. – М.: Издательский центр «Академия», 2004. – 288 с.
14. Прогнозирование и планирование в условиях рынка./ Под редакцией Т.Г. Морозовой, А.В.Пулькина. М.: ЮНИТИ – ДИАНА, 20001 г., 318 с.
15. Сафронова В.М. Прогнозирование и моделирование в социальной работе: Учеб. пособие для студ. высш. учеб. заведений. – М.: Издательский центр «Академия», 2002. – 192с.
16. Смагина И. В. «Статистический анализ демографических процессов в Орловской области на фоне депопуляции населения России»: автореферат диссертации соискание ученой степени кандидата экономических наук www.econ.msu.ru/cmt2/lib/a/839/File/Smagina.doc
17. Смирнова И.В. Демография: Учебно-методическое пособие для студентов специальности «Государственное и муниципальное управление» / филиал СЗАГС в г. Калуга. – Калуга, 2004. – 138 с.
18. Теория управления. Учебник / Уколов В.Ф., Масс А.М., Быстряков И.К. - М.: Экономика, 2003. - 576 с.
19. Указ Президента РФ № 1351 от 9 октября 2007 года «Об утверждении Концепции демографической политики Российской Федерации на период до 2025 года»
20. Черныш Е.А., Молчанова и др. Прогнозирование и планирование. М., 2001 г.
21. Шмойлова Р.А, Минашкин В. Г. Теория статистики- Финансы и Статистика: 2009г., 656стр. Яковлева А.В. Эконометрика: конспект лекций ЭКсмо, 2008
22. Материалы сайтов www.demographia.ru, wikipedia.org.
Приложение 1
Расчет прогнозных значений абсолютного показателя родившихся методом скользящей средней.
| годы | Число родившихся, человек | Скользящая средняя m | Расчет средней относительной ошибки
|
| итого | 37,38 | ||
| 1990 | 33 311 | - | - |
| 1991 | 30 177 | 30 327 | 0,50 |
| 1992 | 27 494 | 27 273 | 0,80 |
| 1993 | 24 148 | 25 367 | 5,05 |
| 1994 | 24 458 | 23 813 | 2,64 |
| 1995 | 22 833 | 22 913 | 0,35 |
| 1996 | 21 449 | 21 724 | 1,28 |
| 1997 | 20 890 | 21 430 | 2,58 |
| 1998 | 21 951 | 20 998 | 4,34 |
| 1999 | 20 154 | 21 193 | 5,16 |
| 2000 | 21 475 | 21 163 | 1,45 |
| 2001 | 21 861 | 22 279 | 1,91 |
| 2002 | 23 500 | 22 934 | 2,41 |
| 2003 | 23 442 | 23 508 | 0,28 |
| 2004 | 23 583 | 23 162 | 1,79 |
| 2005 | 22 460 | 23 126 | 2,97 |
| 2006 | 23 335 | 23 857 | 2,24 |
| 2007 | 25 776 | 25 353 | 1,64 |
| 2008 | 26 947 | 26 155 | |
| прогноз 2009 | 25 743 | 26 148 | |
| прогноз 2010 | 25 754 | ||
| прогноз 2011 | 26 125 | ||
| Средняя относительная ошибка | 2,20 | ||
| Средняя абсолютная ошибка | -85 | ||
| Средняя квадратическая ошибка | 594 | ||
| Расчет прогнозных значений абсолютного показателя умерших методом скользящей средней. | |||
| итого | 22,64 | ||
| 1990 | 20 933 | - | |
| 1991 | 22 469 | 22 507 | 0,17 |
| 1992 | 24 120 | 24 991 | 3,61 |
| 1993 | 28 383 | 27 916 | 1,65 |
| 1994 | 31 244 | 29 887 | 4,34 |
| 1995 | 30 033 | 29 949 | 0,28 |
| 1996 | 28 570 | 28 938 | 1,29 |
| 1997 | 28 210 | 28 406 | 0,70 |
| 1998 | 28 439 | 29 006 | 1,99 |
| 1999 | 30 368 | 30 187 | 0,59 |
| 2000 | 31 755 | 31 472 | 0,89 |
| 2001 | 32 293 | 32 360 | 0,21 |
| 2002 | 33 031 | 32 772 | 0,79 |
| 2003 | 32 991 | 32 781 | 0,64 |
| 2004 | 32 321 | 32 819 | 1,54 |
| 2005 | 33 145 | 32 350 | 2,40 |
| 2006 | 31 583 | 31 909 | 1,03 |
| 2007 | 31 000 | 31 162 | 0,52 |
| 2008 | 30 904 | 31 011 | |
| Прогноз 2009 | 31 130 | 31 040 | |
| Прогноз 2010 | 31 087 | ||
| Прогноз 2011 | 31 026 | ||
| Средняя относительная ошибка | 2,02 | ||
| Средняя абсолютная ошибка | 32 | ||
| Средняя квадратическая ошибка | 795 | ||
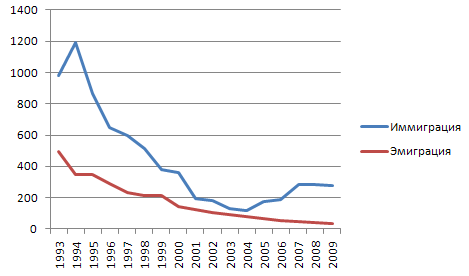
Расчет прогнозных значений абсолютного показателя числа прибывших методом скользящей средней.
| годы | Число прибывших за год | Скользящая средняя m | Расчет средней относительной ошибки
|
| итого | 75,0 | ||
| 1993 | 73131 | ||
| 1994 | 76108 | 73 160 | 3,87 |
| 1995 | 70242 | 68 229 | 2,87 |
| 1996 | 58336 | 62 100 | 6,45 |
| 1997 | 57721 | 55 832 | 3,27 |
| 1998 | 51438 | 52 475 | 2,02 |
| 1999 | 48267 | 47 730 | 1,11 |
| 2000 | 43484 | 41 538 | 4,47 |
| 2001 | 32864 | 35 192 | 7,08 |
| 2002 | 29228 | 30 611 | 4,73 |
| 2003 | 29740 | 29 556 | 0,62 |
| 2004 | 29701 | 30 921 | 4,11 |
| 2005 | 33322 | 30 912 | 7,23 |
| 2006 | 29712 | 31 661 | 6,56 |
| 2007 | 31949 | 29 077 | 8,99 |
| 2008 | 25570 | 28 524 | 11,55 |
| 2009 | 28 053 | 27 658 | 1,41 |
| Прогноз 2010 | 29 352 | 28 499 | |
| Прогноз 2011 | 28 091 | ||
| Прогноз 2012 | 28 078 | ||
| Средняя относительная ошибка | 5 | ||
| Средняя абсолютная ошибка | 11 | ||
| Средняя квадратическая ошибка | 2 177 | ||
Расчет прогнозных значений абсолютного показателя числа выбывших методом скользящей средней.
| годы | Число выбывших за год | Скользящая средняя m | Расчет средней относительной ошибки
|
| итого | 31,0 | ||
| 1993 | 53931 |
| |
| 1994 | 51900 | 54 083 | 4,21 |
| 1995 | 56419 | 53 455 | 5,25 |
| 1996 | 52047 | 51 873 | 0,33 |
| 1997 | 47152 | 47 831 | 1,44 |
| 1998 | 44293 | 45 041 | 1,69 |
| 1999 | 43678 | 42 558 | 2,56 |
| 2000 | 39703 | 39 702 | 0,00 |
| 2001 | 35725 | 36 248 | 1,46 |
| 2002 | 33317 | 34 516 | 3,60 |
| 2003 | 34506 | 33 952 | 1,61 |
| 2004 | 34032 | 34 577 | 1,60 |
| 2005 | 35194 | 34 389 | 2,29 |
| 2006 | 33940 | 34 120 | 0,53 |
| 2007 | 33225 | 32 083 | 3,44 |
| 2008 | 29085 | 29 304 | 0,75 |
| 2009 | 25 603 | 27 611 |
|
| Прогноз 2010 | 28 144 | 27 401 | |
| Прогноз 2011 | 28 457 | ||
| Прогноз 2012 | 27 506 | ||
| Средняя относительная ошибка | 2,05 | ||
| Средняя абсолютная ошибка | 32 | ||
| Средняя квадратическая ошибка | 1 161 | ||
Приложение 2
Расчет прогнозного значения абсолютного показателя родившихся в Оренбургской области методом экпоненциального сглаживания.
| года | Число родившихся, человек | Экспоненциально взвешенная средняя Ut | Расчет средней относительной ошибки
| |||
| Iспособ | IIспособ | I способ | II способ | |||
| 1 | 1990 | 33311 | 24 171 | 33 311 | 27,44 | 0,00 |
| 2 | 1991 | 30177 | 25 085 | 33 311 | 16,87 | 10,39 |
| 3 | 1992 | 27494 | 25 594 | 32 998 | 6,91 | 20,02 |
| 4 | 1993 | 24148 | 25 784 | 32 447 | 6,77 | 34,37 |
| 5 | 1994 | 24458 | 25 620 | 31 617 | 4,75 | 29,27 |
| 6 | 1995 | 22833 | 25 504 | 30 901 | 11,70 | 35,34 |
| 7 | 1996 | 21449 | 25 237 | 30 095 | 17,66 | 40,31 |
| 8 | 1997 | 20890 | 24 858 | 29 230 | 19,00 | 39,92 |
| 9 | 1998 | 21951 | 24 461 | 28 396 | 11,44 | 29,36 |
| 10 | 1999 | 20154 | 24 210 | 27 751 | 20,13 | 37,70 |
| 11 | 2000 | 21475 | 23 805 | 26 992 | 10,85 | 25,69 |
| 12 | 2001 | 21861 | 23 572 | 26 440 | 7,83 | 20,95 |
| 13 | 2002 | 23500 | 23 401 | 25 982 | 0,42 | 10,56 |
| 14 | 2003 | 23442 | 23 411 | 25 734 | 0,13 | 9,78 |
| 15 | 2004 | 23583 | 23 414 | 25 505 | 0,72 | 8,15 |
| 16 | 2005 | 22460 | 23 431 | 25 313 | 4,32 | 12,70 |
| 17 | 2006 | 23335 | 23 334 | 25 027 | 0,01 | 7,25 |
| 18 | 2007 | 25776 | 23 334 | 24 858 | 9,47 | 3,56 |
| 19 | 2008 | 26947 | 23 578 | 24 950 | 12,50 | 7,41 |
| прогноз | 2009 | 23 915 | 25 150 | |||
| итого | 459 244 | 188,92 | 382,72 | |||
| Средняя относительная ошибка ɛ | 9,94 | 20,14 | ||||
| Средняя абсолютная ошибка Δ | -135 | -4 296 | ||||
| Средняя квадратическая ошибка | 3 275 | 5 386 | ||||
Расчет прогнозного значения абсолютного показателя умерших в Оренбургской области методом экпоненциального сглаживания.
| года | Число умерших, человек | Экспоненциально взвешенная средняя Ut | Расчет средней относительной ошибки
| |||
| Iспособ | IIспособ | I способ | II способ | |||
| 1 | 1990 | 20933 | 29 795 | 20 933 | 2,34 | 0,00 |
| 2 | 1991 | 22469 | 28 909 | 20 933 | 28,66 | 6,84 |
| 3 | 1992 | 28 439 | 28 265 | 21 087 | 0,61 | 25,85 |
| 4 | 1993 | 28383 | 28 282 | 21 822 | 0,35 | 23,12 |
| 5 | 1994 | 31244 | 28 293 | 22 478 | 9,45 | 28,06 |
| 6 | 1995 | 30033 | 28 588 | 23 355 | 4,81 | 22,24 |
| 7 | 1996 | 28570 | 28 732 | 24 022 | 0,57 | 15,92 |
| 8 | 1997 | 28210 | 28 716 | 24 477 | 1,79 | 13,23 |
| 9 | 1998 | 28439 | 28 665 | 24 850 | 0,80 | 12,62 |
| 10 | 1999 | 30368 | 28 643 | 25 209 | 5,68 | 16,99 |
| 11 | 2000 | 31755 | 28 815 | 25 725 | 9,26 | 18,99 |
| 12 | 2001 | 32293 | 29 109 | 26 328 | 9,86 | 18,47 |
| 13 | 2002 | 33031 | 29 428 | 26 925 | 10,91 | 18,49 |
| 14 | 2003 | 32991 | 29 788 | 27 535 | 9,71 | 16,54 |
| 15 | 2004 | 32321 | 30 108 | 28 081 | 6,85 | 13,12 |
| 16 | 2005 | 33145 | 30 330 | 28 505 | 8,49 | 14,00 |
| 17 | 2006 | 31583 | 30 611 | 28 969 | 3,08 | 8,28 |
| 18 | 2007 | 31000 | 30 708 | 29 230 | 0,94 | 5,71 |
| 19 | 2008 | 30904 | 30 737 | 29 407 | 0,54 | 4,84 |
| прогноз | 2009 | 30 754 | 29 557 | |||
| итого | 566 111 | 154,69 | 283,29 | |||
| Средняя относительная ошибка ɛ | 8,14 | 14,91 | ||||
| Средняя абсолютная ошибка Δ | 64 | 1241 | ||||
| Средняя квадратическая ошибка | 2 571 | 2 965 | ||||
Расчет прогнозного значения абсолютного показателя прибывших в Оренбургской области методом экпоненциального сглаживания.
| года | Число прибывших, человек | Экспоненциально взвешенная средняя Ut | Расчет средней относительной ошибки
| |||
| Iспособ | IIспособ | I способ | II способ | |||
| 1 | 1993 | 73131 | 44 051 | 73 131 | 39,76 | 0,00 |
| 2 | 1994 | 76108 | 47 282 | 73 131 | 37,88 | 3,91 |
| 3 | 1995 | 70242 | 50 485 | 73 462 | 28,13 | 4,58 |
| 4 | 1996 | 58336 | 52 680 | 73 104 | 9,70 | 25,32 |
| 5 | 1997 | 57721 | 53 309 | 71 463 | 7,64 | 23,81 |
| 6 | 1998 | 51438 | 53 799 | 69 936 | 4,59 | 35,96 |
| 7 | 1999 | 48267 | 53 537 | 67 881 | 10,92 | 40,64 |
| 8 | 2000 | 43484 | 52 951 | 65 702 | 21,77 | 51,09 |
| 9 | 2001 | 32864 | 51 899 | 63 233 | 57,92 | 92,41 |
| 10 | 2002 | 29228 | 49 784 | 59 859 | 70,33 | 104,80 |
| 11 | 2003 | 29740 | 47 500 | 56 455 | 59,72 | 89,83 |
| 12 | 2004 | 29701 | 45 527 | 53 487 | 53,28 | 80,08 |
| 13 | 2005 | 33322 | 43 768 | 50 844 | 31,35 | 52,58 |
| 14 | 2006 | 29712 | 42 608 | 48 897 | 43,40 | 64,57 |
| 15 | 2007 | 31949 | 41 175 | 46 765 | 28,88 | 46,38 |
| 16 | 2008 | 25570 | 40 150 | 45 119 | 57,02 | 76,45 |
| 17 | 2009 | 28053 | 38 530 | 42 947 | 37,35 | 53,09 |
| прогноз | 2010 | 37 366 | 41 292 | |||
| итого | 748866 | 599,6 | 845,51 | |||
| Средняя относительная ошибка ɛ | 35,27 | 49,74 | ||||
| Средняя абсолютная ошибка Δ | -3 539 | -16 856 | ||||
| Средняя квадратическая ошибка | 15 857 | 19 228 | ||||
Расчет прогнозного значения абсолютного показателя выбывших в Оренбургской области методом экпоненциального сглаживания.
| года | Число выбывших, человек | Экспоненциально взвешенная средняя Ut | Расчет средней относительной ошибки
| |||
| Iспособ | IIспособ | I способ | II способ | |||
| 1 | 1993 | 53931 | 40 221 | 53 931 | 25,42 | 0,00 |
| 2 | 1994 | 51900 | 41 744 | 53 931 | 19,57 | 3,91 |
| 3 | 1995 | 56419 | 42 872 | 53 705 | 24,01 | 4,81 |
| 4 | 1996 | 52047 | 44 378 | 54 007 | 14,74 | 3,77 |
| 5 | 1997 | 47152 | 45 230 | 53 789 | 4,08 | 14,08 |
| 6 | 1998 | 44293 | 45 443 | 53 052 | 2,60 | 19,77 |
| 7 | 1999 | 43678 | 45 316 | 52 078 | 3,75 | 19,23 |
| 8 | 2000 | 39703 | 45 134 | 51 145 | 13,68 | 28,82 |
| 9 | 2001 | 35725 | 44 530 | 49 874 | 24,65 | 39,60 |
| 10 | 2002 | 33317 | 43 552 | 48 302 | 30,72 | 44,98 |
| 11 | 2003 | 34506 | 42 415 | 46 637 | 22,92 | 35,16 |
| 12 | 2004 | 34032 | 41 536 | 45 289 | 22,05 | 33,08 |
| 13 | 2005 | 35194 | 40 702 | 44 038 | 15,65 | 25,13 |
| 14 | 2006 | 33940 | 40 090 | 43 055 | 18,12 | 26,86 |
| 15 | 2007 | 33225 | 39 407 | 42 043 | 18,61 | 26,54 |
| 16 | 2008 | 29085 | 38 720 | 41 063 | 33,13 | 41,18 |
| 17 | 2009 | 25603 | 37 649 | 39 732 | 47,05 | 55,18 |
| прогноз | 2010 | 36 311 | 38 162 | |||
| итого | 683750 | 340,73 | 422,10 | |||
| Средняя относительная ошибка ɛ | 20,04 | 24,83 | ||||
| Средняя абсолютная ошибка Δ | -2070 | -8348 | ||||
| Средняя квадратическая ошибка | 8458 | 9757 | ||||
Приложение 3
Расчет параметров параболического тренда для абсолютного показателя численности населения в Оренбургской области.
| годы | Численность населения, человек | Условное обозначение времени t |
|
| Тренд |
| 1990 | 2 151 097 | -9,5 | -20 435 422 | 194 136 504 | 2 150 906 |
| 1991 | 2 159 743 | -8,5 | -18 357 816 | 156 041 432 | 2 165 143 |
| 1992 | 2 168 257 | -7,5 | -16 261 928 | 121 964 456 | 2 177 454 |
| 1993 | 2 182 602 | -6,5 | -14 186 913 | 92 214 935 | 2 187 841 |
| 1994 | 2 196 785 | -5,5 | -12 082 318 | 66 452 746 | 2 196 303 |
| 1995 | 2 213 038 | -4,5 | -9 958 671 | 44 814 020 | 2 202 840 |
| 1996 | 2 218 052 | -3,5 | -7 763 182 | 27 171 137 | 2 207 452 |
| 1997 | 2 215 936 | -2,5 | -5 539 840 | 13 849 600 | 2 210 139 |
| 1998 | 2 218 082 | -1,5 | -3 327 123 | 4 990 685 | 2 210 901 |
| 1999 | 2 217 558 | -0,5 | -1 108 779 | 554 390 | 2 209 738 |
| 2000 | 2 211 204 | 0,5 | 1 105 602 | 552 801 | 2 206 651 |
| 2001 | 2 203 616 | 1,5 | 3 305 424 | 4 958 136 | 2 201 638 |
| 2002 | 2 189 876 | 2,5 | 5 474 690 | 13 686 725 | 2 194 701 |
| 2003 | 2 176 000 | 3,5 | 7 616 000 | 26 656 000 | 2 185 839 |
| 2004 | 2 162 545 | 4,5 | 9 731 453 | 43 791 536 | 2 175 052 |
| 2005 | 2 150 407 | 5,5 | 11 827 239 | 65 049 812 | 2 162 340 |
| 2006 | 2 137 850 | 6,5 | 13 896 025 | 90 324 163 | 2 147 703 |
| 2007 | 2 125 503 | 7,5 | 15 941 273 | 119 559 544 | 2 131 141 |
| 2008 | 2 119 003 | 8,5 | 18 011 526 | 153 097 967 | 2 112 655 |
| 2009 | 2 111 531 | 9,5 | 20 059 545 | 190 565 673 | 2 092 243 |
| Итого | 43 528 685 | 0 | -2 053 216 | 1 430 432 259 | 2 150 906 |
Три частные производные функции: 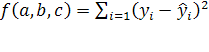 приравниваются к нулю, и после преобразований получаем систему трех уравнений с тремя неизвестными:
приравниваются к нулю, и после преобразований получаем систему трех уравнений с тремя неизвестными:
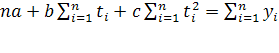 (11)
(11)
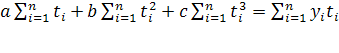 (12)
(12)
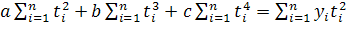 (13)
(13)
При переносе начала отсчета периодов (моментов) времени в середину ряда суммы нечетных степеней номеров этих периодов ![]() и
и ![]() обращаются в нуль. При этом второе уравнение обращается в уравнение с одним неизвестным, откуда:
обращаются в нуль. При этом второе уравнение обращается в уравнение с одним неизвестным, откуда: 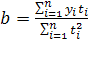
Уравнения (11) и (13) образуют систему двух уравнений с двумя неизвестными:
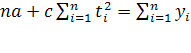 (14)
(14)
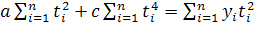 (15)
(15)
Где 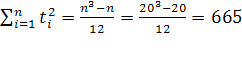 ;
; 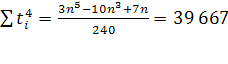
По данным таблицы вычисляем параметры:
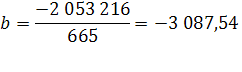
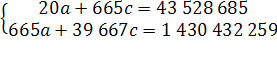
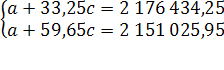
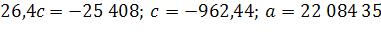
Расчет прогнозных значений показателя численности населения в Оренбургской области, величин средней относительной ошибки ɛ, среднего квадратического отклонения уровней ряда от тренда S(t).
| годы | Числен-ность населения, человек | Условное обозна- чение времени t |
|
| Тренд
| Расчет средней относительной ошибки
|
|
| 1990 | 2 151 097 | -9,5 | 90,25 | 8 145,06 | 2 150 906 | 0,01 | 36 313,11 |
| 1991 | 2 159 743 | -8,5 | 72,25 | 5 220,06 | 2 165 143 | 0,25 | 29 158 033,30 |
| 1992 | 2 168 257 | -7,5 | 56,25 | 3 164,06 | 2 177 454 | 0,42 | 84 590 617,73 |
| 1993 | 2 182 602 | -6,5 | 42,25 | 1 785,06 | 2 187 841 | 0,24 | 27 446 426,15 |
| 1994 | 2 196 785 | -5,5 | 30,25 | 915,06 | 2 196 303 | 0,02 | 232 640,71 |
| 1995 | 2 213 038 | -4,5 | 20,25 | 410,06 | 2 202 840 | 0,46 | 104 008 801,08 |
| 1996 | 2 218 052 | -3,5 | 12,25 | 150,06 | 2 207 452 | 0,48 | 112 370 444,03 |
| 1997 | 2 215 936 | -2,5 | 6,25 | 39,06 | 2 210 139 | 0,26 | 33 609 785,73 |
| 1998 | 2 218 082 | -1,5 | 2,25 | 5,06 | 2 210 901 | 0,32 | 51 569 300,84 |
| 1999 | 2 217 558 | -0,5 | 0,25 | 0,06 | 2 209 738 | 0,35 | 61 149 881,16 |
| 2000 | 2 211 204 | 0,5 | 0,25 | 0,06 | 2 206 651 | 0,21 | 20 733 279,01 |
| 2001 | 2 203 616 | 1,5 | 2,25 | 5,06 | 2 201 638 | 0,09 | 3 911 705,33 |
| 2002 | 2 189 876 | 2,5 | 6,25 | 39,06 | 2 194 701 | 0,22 | 23 279 609,22 |
| 2003 | 2 176 000 | 3,5 | 12,25 | 150,06 | 2 185 839 | 0,45 | 96 800 266,25 |
| 2004 | 2 162 545 | 4,5 | 20,25 | 410,06 | 2 175 052 | 0,58 | 156 416 307,39 |
| 2005 | 2 150 407 | 5,5 | 30,25 | 915,06 | 2 162 340 | 0,55 | 142 389 530,26 |
| 2006 | 2 137 850 | 6,5 | 42,25 | 1 785,06 | 2 147 703 | 0,46 | 97 079 368,75 |
| 2007 | 2 125 503 | 7,5 | 56,25 | 3 164,06 | 2 131 141 | 0,27 | 31 789 121,19 |
| 2008 | 2 119 003 | 8,5 | 72,25 | 5 220,06 | 2 112 655 | 0,30 | 40 302 155,83 |
| 2009 | 2 111 531 | 9,5 | 90,25 | 8 145,06 | 2 092 243 | 0,91 | 372 021 543,38 |
| Итого | 43 528 685 | 0 | 665 | 39 667 | 2 150 906 | 0,34 | 1 488 895 130 |
| Ср.зн. | 2 176 434 | 33,25 | 1 983,36 |
Для показателя числа родившихся функцией тренда лучше всего аппроксимирующей временной ряд также является парабола II порядка:
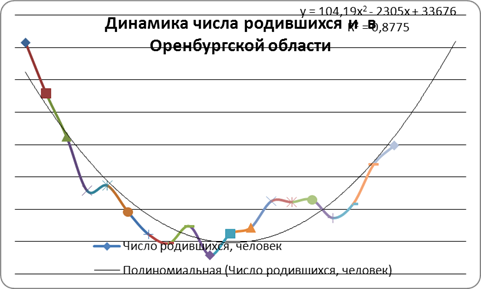
Рис. 3. Динамика числа родившихся в Оренбургской области с полиномиальной линией тренда.
Расчет параметров параболического тренда для абсолютного показателя числа родившихся в Оренбургской области.
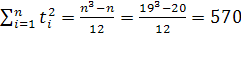 ;
; 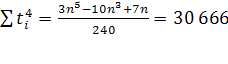
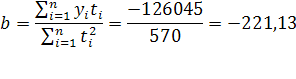
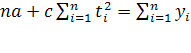
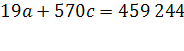
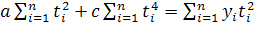
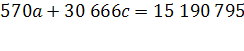
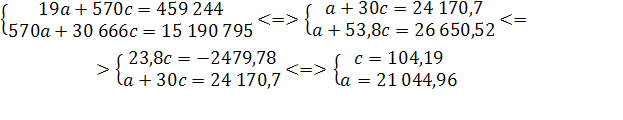
Уравнение регрессии:
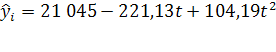 , где
, где ![]() =0 в 1999г.
=0 в 1999г.
Среднее квадратическое отклонение:
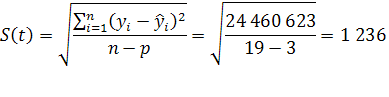
Средняя ошибка репрезентативности выборочной оценки параметра с:
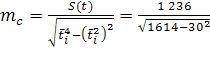 =46,27
=46,27
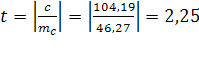
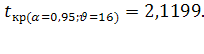
Фактическая величина t-критерия 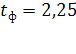 больше табличного
больше табличного 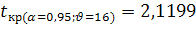 , следовательно, вероятность нулевой гипотезы (о равенстве параметра с нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность числа родившихся в Оренбургской области снижалась не случайно.
, следовательно, вероятность нулевой гипотезы (о равенстве параметра с нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность числа родившихся в Оренбургской области снижалась не случайно.
Средняя ошибка прогноза положения параболического тренда на период с номером ![]() :
:
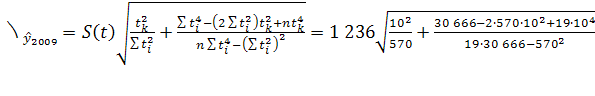 =949
=949
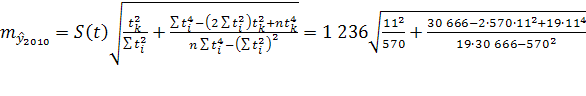 =1 156
=1 156
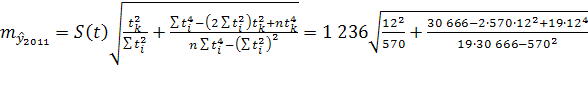 =1 390
=1 390
Средняя ошибка прогноза:
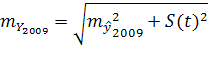 =
=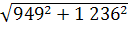 = 1 558
= 1 558
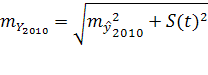 =
=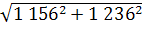 = 1 693
= 1 693
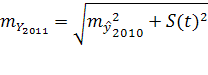 =
=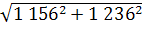 = 1 860
= 1 860
Вероятная ошибка прогноза:
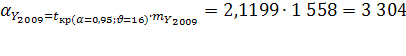
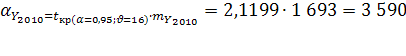
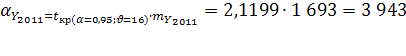
Прогнозные значения:
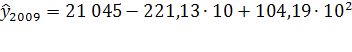 =29 253
=29 253
Доверительный интервал (25 949; 32 557)
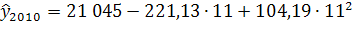 =31 220
=31 220
Доверительный интервал (27 630; 34 809)
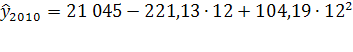 =33 395
=33 395
Доверительный интервал (29 452; 37 338)
Как видно по полученным данным, при сохранении имеющейся тенденции, число родившихся продолжит расти и вероятно в 2011 году превысит максимальный уровень в наблюдаемом периоде (1990г.)
Средняя относительная ошибка:
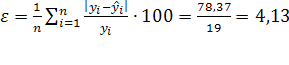 прогноз обладает высокой точностью.
прогноз обладает высокой точностью.
| годы | Число родив-шихся, человек | Условное обозначение времени t |
|
|
|
| Тренд | Расчет средней относительной ошибки
|
|
| 1990 | 33 311 | -9 | 81 | 6561 | -299799 | 2698191 | 31 474,74 | 5,51 | 3 371 862,39 |
| 1991 | 30 177 | -8 | 64 | 4096 | -241416 | 1931328 | 29 482,33 | 2,30 | 482 561,78 |
| 1992 | 27 494 | -7 | 49 | 2401 | -192458 | 1347206 | 27 698,31 | 0,74 | 41 744,52 |
| 1993 | 24 148 | -6 | 36 | 1296 | -144888 | 869328 | 26 122,68 | 8,18 | 3 899 365,50 |
| 1994 | 24 458 | -5 | 25 | 625 | -122290 | 611450 | 24 755,43 | 1,22 | 88 466,04 |
| 1995 | 22 833 | -4 | 16 | 256 | -91332 | 365328 | 23 596,57 | 3,34 | 583 037,05 |
| 1996 | 21 449 | -3 | 9 | 81 | -64347 | 193041 | 22 646,09 | 5,58 | 1 433 023,95 |
| 1997 | 20 890 | -2 | 4 | 16 | -41780 | 83560 | 21 904,00 | 4,85 | 1 028 187,63 |
| 1998 | 21 951 | -1 | 1 | 1 | -21951 | 21951 | 21 370,29 | 2,65 | 337 227,71 |
| 1999 | 20 154 | 0 | 0 | 0 | 0 | 0 | 21 044,96 | 4,42 | 793 814,80 |
| 2000 | 21 475 | 1 | 1 | 1 | 21475 | 21475 | 20 928,02 | 2,55 | 299 183,03 |
| 2001 | 21 861 | 2 | 4 | 16 | 43722 | 87444 | 21 019,47 | 3,85 | 708 173,49 |
| 2002 | 23 500 | 3 | 9 | 81 | 70500 | 211500 | 21 319,30 | 9,28 | 4 755 451,14 |
| 2003 | 23 442 | 4 | 16 | 256 | 93768 | 375072 | 21 827,52 | 6,89 | 2 606 558,60 |
| 2004 | 23 583 | 5 | 25 | 625 | 117915 | 589575 | 22 544,12 | 4,41 | 1 079 278,69 |
| 2005 | 22 460 | 6 | 36 | 1296 | 134760 | 808560 | 23 469,10 | 4,49 | 1 018 287,18 |
| 2006 | 23 335 | 7 | 49 | 2401 | 163345 | 1143415 | 24 602,47 | 5,43 | 1 606 486,92 |
| 2007 | 25 776 | 8 | 64 | 4096 | 206208 | 1649664 | 25 944,23 | 0,65 | 28 300,68 |
| 2008 | 26 947 | 9 | 81 | 6561 | 242523 | 2182707 | 27 494,37 | 2,03 | 299 612,19 |
| Итого | 459 244 | 0 | 570 | 30 666 | -126 045 | 15 190 795 | 459 244,00 | 78,37 | 24 460 623 |
| Ср. Знач. | 30 | 1614 |
Расчет параметров параболического тренда для абсолютного показателя числа умерших в Оренбургской области.
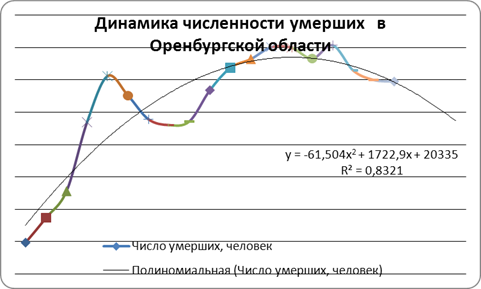
Рис. 4. Динамика числа умерших в Оренбургской области с полиномиальной линией тренда.
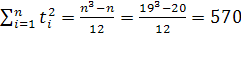 ;
; 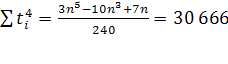
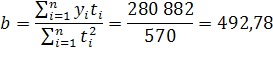
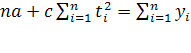
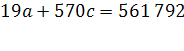
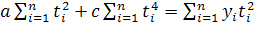
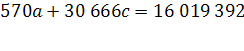
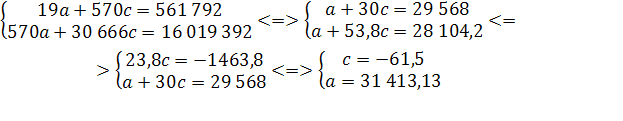
Уравнение регрессии:
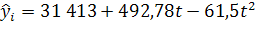 , где
, где ![]() =0 в 1999г.
=0 в 1999г.
Среднее квадратическое отклонение:
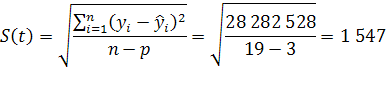
Средняя ошибка прогноза положения параболического тренда на период с номером ![]() :
:
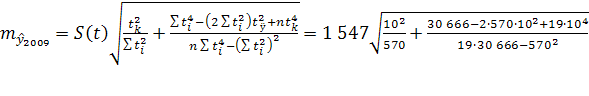 =1 187
=1 187
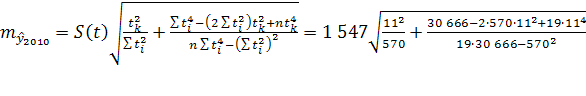 =1 447
=1 447
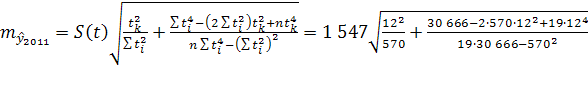 =1 739
=1 739
Средняя ошибка прогноза:
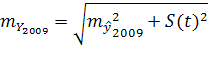 =
=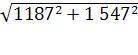 = 1 950
= 1 950
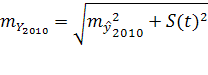 =
=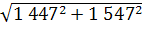 = 2 118
= 2 118
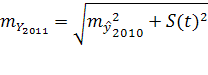 =
=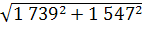 = 2 327
= 2 327
Вероятная ошибка прогноза:
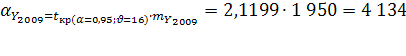
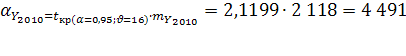
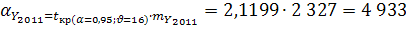
Прогнозные значения:
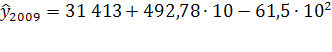 =30 190
=30 190
Доверительный интервал (26 057; 34 324)
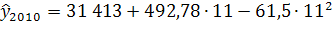 =29 392
=29 392
Доверительный интервал (25 258; 33 525)
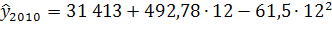 =28 470
=28 470
Доверительный интервал (24 336; 32 604)
При сохранении имеющейся тенденции, число умерших будет снижаться.
Средняя относительная ошибка:
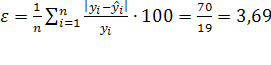
прогноз обладает высокой точностью.
| годы | Число умерших, человек | Условное обозначение времени t |
|
|
|
| Тренд | Расчет средней относительной ошибки
|
|
| 1990 | 20 933 | -9 | 81 | 6561 | -188397 | 1695573 | -332 202 | 5,08 | 1 130 605,29 |
| 1991 | 22 469 | -8 | 64 | 4096 | -179752 | 1438016 | -188 971 | 4,74 | 1 135 606,98 |
| 1992 | 24 120 | -7 | 49 | 2401 | -168840 | 1181880 | -92 113 | 3,44 | 688 882,23 |
| 1993 | 28 383 | -6 | 36 | 1296 | -170298 | 1021788 | -30 557 | 7,54 | 4 582 505,41 |
| 1994 | 31 244 | -5 | 25 | 625 | -156220 | 781100 | 5 292 | 12,27 | 14 686 948,28 |
| 1995 | 30 033 | -4 | 16 | 256 | -120132 | 480528 | 23 552 | 5,24 | 2 480 753,73 |
| 1996 | 28 570 | -3 | 9 | 81 | -85710 | 257130 | 30 866 | 2,84 | 658 150,93 |
| 1997 | 28 210 | -2 | 4 | 16 | -56420 | 112840 | 32 400 | 6,99 | 3 887 057,51 |
| 1998 | 28 439 | -1 | 1 | 1 | -28439 | 28439 | 31 844 | 8,51 | 5 855 677,34 |
| 1999 | 30 368 | 0 | 0 | 0 | 0 | 0 | 31 413 | 3,44 | 1 092 297,71 |
| 2000 | 31 755 | 1 | 1 | 1 | 31755 | 31755 | 31 844 | 0,28 | 7 992,64 |
| 2001 | 32 293 | 2 | 4 | 16 | 64586 | 129172 | 32 400 | 0,43 | 19 694,21 |
| 2002 | 33 031 | 3 | 9 | 81 | 99093 | 297279 | 30 866 | 2,10 | 480 363,15 |
| 2003 | 32 991 | 4 | 16 | 256 | 131964 | 527856 | 23 552 | 1,79 | 349 088,78 |
| 2004 | 32 321 | 5 | 25 | 625 | 161605 | 808025 | 5 292 | 0,06 | 338,52 |
| 2005 | 33 145 | 6 | 36 | 1296 | 198870 | 1193220 | -30 557 | 2,98 | 978 859,85 |
| 2006 | 31 583 | 7 | 49 | 2401 | 221081 | 1547567 | -92 113 | 0,84 | 70 673,80 |
| 2007 | 31 000 | 8 | 64 | 4096 | 248000 | 1984000 | -188 971 | 1,35 | 175 607,63 |
| 2008 | 30 904 | 9 | 81 | 6561 | 278136 | 2503224 | -332 202 | 0,12 | 1 424,52 |
| Итого | 561 792 | 0 | 570 | 30 666 | 280 882 | 16 019 392 | -1 008 361 | 70 | 38 282 528 |
| Ср. Знач. | 30 | 1614 |
Расчет параметров параболического тренда для абсолютного показателя числа прибывших в Оренбургской области.
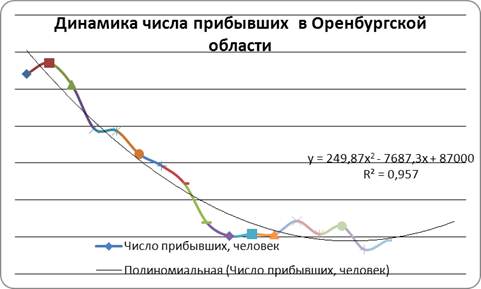
Рис. 5. Динамика числа прибывших в Оренбургской области с полиномиальной линией тренда.
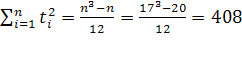 ;
; 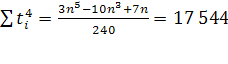
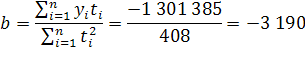
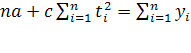
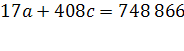
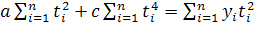
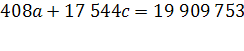
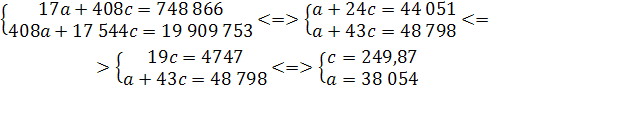
Уравнение регрессии:
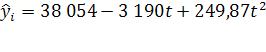 , где
, где ![]() =0 в 2001г.
=0 в 2001г.
Среднее квадратическое отклонение:
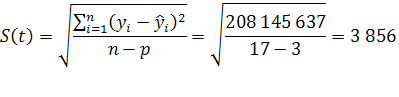
Средняя ошибка прогноза положения параболического тренда на период с номером ![]() :
:
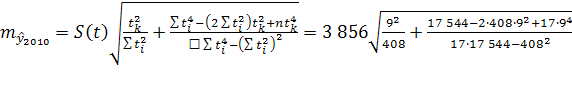 =3 171
=3 171
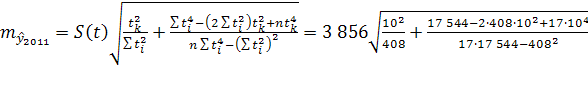 = 3 949
= 3 949
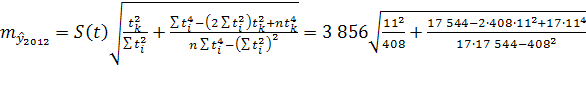 =4830
=4830
Средняя ошибка прогноза:
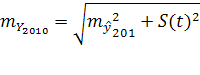 =
=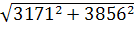 =4 992
=4 992
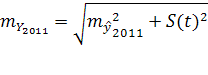 =
=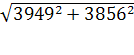 = 5519
= 5519
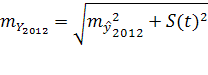 =
=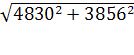 = 6 180
= 6 180
Вероятная ошибка прогноза:
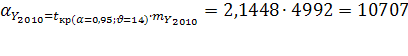
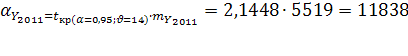
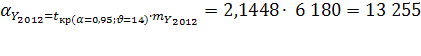
Прогнозные значения:
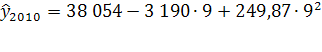 =29 586
=29 586
Доверительный интервал (18 878; 40 294)
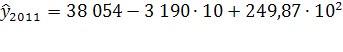 =31 144
=31 144
Доверительный интервал (19 306; 42 982)
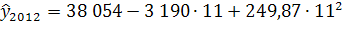 =33 202
=33 202
Доверительный интервал (19 946; 46 457)
Средняя относительная ошибка:
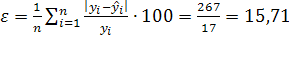 прогноз обладает высокой точностью.
прогноз обладает высокой точностью.
| годы | Число прибывших, человек | Условное обозначение времени t |
|
|
|
| Тренд | Расчет средней относительной ошибки
|
|
| 1993 | 73131 | -8 | 64 | 4096 | -585048 | 4680384 | 79 563 | 8,80 | 41 370 292,11 |
| 1994 | 76108 | -7 | 49 | 2401 | -532756 | 3729292 | 72 625 | 4,58 | 12 129 198,93 |
| 1995 | 70242 | -6 | 36 | 1296 | -421452 | 2528712 | 66 187 | 5,77 | 16 440 106,28 |
| 1996 | 58336 | -5 | 25 | 625 | -291680 | 1458400 | 60 249 | 3,28 | 3 660 157,34 |
| 1997 | 57721 | -4 | 16 | 256 | -230884 | 923536 | 54 811 | 5,04 | 8 469 953,01 |
| 1998 | 51438 | -3 | 9 | 81 | -154314 | 462942 | 49 872 | 3,04 | 2 452 532,97 |
| 1999 | 48267 | -2 | 4 | 16 | -96534 | 193068 | 45 433 | 5,87 | 8 031 899,65 |
| 2000 | 43484 | -1 | 1 | 1 | -43484 | 43484 | 41 494 | 4,58 | 3 961 416,51 |
| 2001 | 32864 | 0 | 0 | 0 | 0 | 0 | 38 054 | 15,79 | 26 937 481,88 |
| 2002 | 29228 | 1 | 1 | 1 | 29228 | 29228 | 35 114 | 20,14 | 34 648 892,78 |
| 2003 | 29740 | 2 | 4 | 16 | 59480 | 118960 | 32 674 | 9,87 | 8 609 898,77 |
| 2004 | 29701 | 3 | 9 | 81 | 89103 | 267309 | 30 734 | 3,48 | 1 066 941,89 |
| 2005 | 33322 | 4 | 16 | 256 | 133288 | 533152 | 29 293 | 12,09 | 16 230 192,53 |
| 2006 | 29712 | 5 | 25 | 625 | 148560 | 742800 | 28 352 | 4,58 | 1 848 341,97 |
| 2007 | 31949 | 6 | 36 | 1296 | 191694 | 1150164 | 27 911 | 12,64 | 16 302 775,03 |
| 2008 | 25570 | 7 | 49 | 2401 | 178990 | 1252930 | 27 970 | 9,39 | 5 759 675,55 |
| 2009 | 28053 | 8 | 64 | 4096 | 224424 | 1795392 | 28 528 | 1,69 | 225 879,97 |
| Итого | 561 792 | 0 | 408 | 17 544 | -1 301 385 | 19 909 753 | 748 866 | 131 | 208 145 637 |
| Ср. зн. | 24 | 1032 |
Расчет параметров линейного тренда для абсолютного показателя числа выбывших в Оренбургской области.
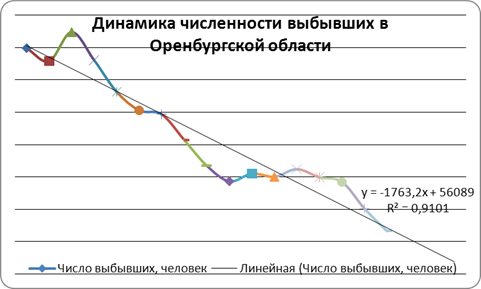
Рис. 6. Динамика числа выбывших в Оренбургской области с линейной линией тренда.
Уравнение имеет вид: 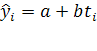 ,
,
Где ![]() - уровень тренда для периода или момента с номером
- уровень тренда для периода или момента с номером ![]() ;
;
а - свободный член уравнения, равный среднего уровню тренда для периода (момента) с нулевым номером ![]() ;
;
b – главный параметр линейного тренда, его константа, среднее абсолютное изменение за принятую в ряду единицу времени.
Уравнения метода наименьших квадратов:
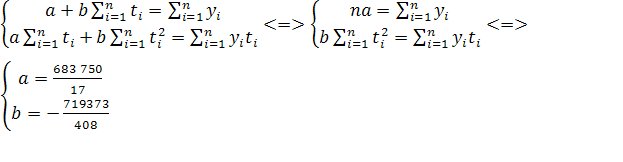
Откуда а = 40 220, b = -1 763
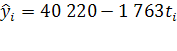 , t=0 в 2001году
, t=0 в 2001году
| годы | Число выбывших, человек | Условное обозначение времени t | t2 |
| Тренд | Расчет средней относительной ошибки
|
| 1993 | 53931 | -8 | 64 | -431448 | 56 563 | 4,88 |
| 1994 | 51900 | -7 | 49 | -363300 | 53 961 | 3,97 |
| 1995 | 56419 | -6 | 36 | -338514 | 51 471 | 8,77 |
| 1996 | 52047 | -5 | 25 | -260235 | 49 092 | 5,68 |
| 1997 | 47152 | -4 | 16 | -188608 | 46 826 | 0,69 |
| 1998 | 44293 | -3 | 9 | -132879 | 44 671 | 0,85 |
| 1999 | 43678 | -2 | 4 | -87356 | 42 628 | 2,40 |
| 2000 | 39703 | -1 | 1 | -39703 | 40 698 | 2,51 |
| 2001 | 35725 | 0 | 0 | 0 | 38 878 | 8,83 |
| 2002 | 33317 | 1 | 1 | 33317 | 37 171 | 11,57 |
| 2003 | 34506 | 2 | 4 | 69012 | 35 576 | 3,10 |
| 2004 | 34032 | 3 | 9 | 102096 | 34 092 | 0,18 |
| 2005 | 35194 | 4 | 16 | 140776 | 32 721 | 7,03 |
| 2006 | 33940 | 5 | 25 | 169700 | 31 461 | 7,30 |
| 2007 | 33225 | 6 | 36 | 199350 | 30 313 | 8,76 |
| 2008 | 29085 | 7 | 49 | 203595 | 29 276 | 0,66 |
| 2009 | 25603 | 8 | 64 | 204824 | 28 352 | 10,74 |
| Итого | 683 750 | 0 | 408 | -719 373 | 683 750 | 88 |
Средняя ошибка прогноза положения о тренда на период с номером ![]() от середины базы расчета тренда имеет вид:
от середины базы расчета тренда имеет вид:
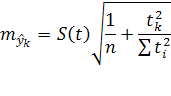
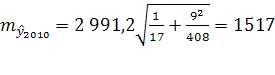
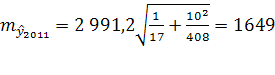
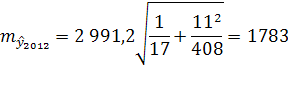
Средняя ошибка прогноза
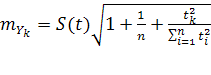
Вероятная ошибка прогноза:
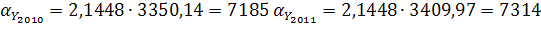
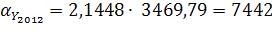
Прогнозные значения:
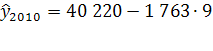 =24 352
=24 352 ![]() (17 166; 31 537)
(17 166; 31 537)
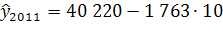 =22 589
=22 589 ![]() (15 275; 29 902)
(15 275; 29 902)
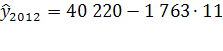 = 20 826
= 20 826 ![]() (13 383; 28 267).
(13 383; 28 267).
Средняя относительная ошибка:
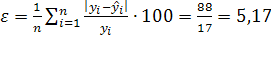
прогноз обладает высокой точностью.
Похожие работы
... ситуации в стране , из-за высокой инфляции и т. д. И только в последние годы государство стало выделять необходимые суммы на реализацию миграционной программы. 2.3 Программирование миграционных процессов на региональном уровне (па примере Пензенской области) В целях обеспечения реализации государственной миграционной политики на территории области была принята и реализована « Целевая ...
... Заславская, В.А. Коптюг, В.А. Костин, В.М. Кудров, Ю.С. Левада, Г.В. Осипов, П.Д. Тавленок, А.С. Панарин, Н.М. Римашевская, Ж.Т. Тощенко, О.И. Шкаратан, В.А. Ядов и др. Глава 2. Эволюция социального прогнозирования 2.1 Социальное прогнозирование на рубеже XIX—XX столетий Важный сдвиг в развитии представлений о будущем сыграла роль научная фантастика (произведения Брэдбери, Кларка, Шекли, ...
... , благотворительными и религиозными организациями, а также предусмотреть активное участие самого населения. 3 Основные направления улучшения демографической ситуации и эффективности использования трудовых ресурсов Октябрьского района Волгоградской области 3.1 Анализ социально-экономического развития Октябрьского района Октябрьский район расположен в южной части Волгоградской области. ...
... (оценки, мнения, восприятие и т.д.), а также неадекватную, искаженную информацию о действительности, основанную на стереотипах, слухах и других подобных источниках. Поэтому используемая в технологиях социального прогнозирования информация, входящая в прогнозный блок, должна быть полной, достоверной, актуальной и обладать следующими свойствами: I) атрибутивными (единство материального и социального ...
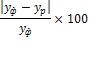
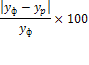
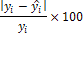

0 комментариев